Calculus 2 Lecture 6.6: A Discussion of Hyperbolic Functions
TLDRThe transcript discusses hyperbolic functions, their definitions, and their similarities to trigonometric functions. It delves into the properties and identities of hyperbolic functions, such as the hyperbolic cosine and tangent, and their applications in real-life scenarios like engineering. The video covers the derivation of these functions, highlighting the process of finding derivatives using chain and product rules, and emphasizes the importance of understanding these concepts for further studies in calculus.
Takeaways
- 📚 The lesson covers hyperbolic functions, which are similar to trigonometric functions and are used in real-life applications like engineering.
- 🔍 Hyperbolic functions include hyperbolic sine (cosh), hyperbolic cosine (sinh), hyperbolic tangent (tanh), and others, derived from the exponential function.
- 🌐 The script explains that hyperbolic functions can be applied to real-world scenarios, such as the curving of electric wires, based on hyperbolic functions.
- 📊 The identities of hyperbolic functions are introduced, highlighting their similarities to trigonometric identities but with slight differences.
- 🛠️ The lesson provides examples of how to use the identities and definitions to derive properties and solve problems involving hyperbolic functions.
- 📈 The derivatives of hyperbolic functions are discussed, with examples and proofs to show how they can be calculated using chain rule and other calculus techniques.
- 🧩 The script emphasizes the importance of practice and familiarity with the new concepts, encouraging students to use flashcards and practice problems.
- 🔄 The lesson also touches on inverse hyperbolic functions, explaining that they exist due to the one-to-one nature of hyperbolic functions and providing their logarithmic forms.
- 📝 A detailed example is worked out for finding the derivative of the inverse hyperbolic cosine function, using algebraic manipulation and the chain rule.
- 🚀 The concept of double-angle identities for hyperbolic functions is introduced, showing how they can be derived and proven.
- 📚 The lesson concludes with a brief mention of upcoming topics, including more on derivatives and integrals of hyperbolic functions, and a teaser for inverse hyperbolic functions.
Q & A
What are hyperbolic functions and why are they covered in the same section as inverses?
-Hyperbolic functions are mathematical functions that resemble trigonometric functions in behavior, hence they are sometimes referred to as hyperbolic trigonometric functions. They are covered in the same section as inverses because, like trigonometric functions, hyperbolic functions also have inverses that share similar properties.
What is the definition of the hyperbolic cosine function?
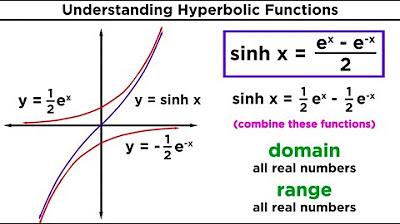
-The hyperbolic cosine function, denoted as cosh(x), is defined as (e^x + e^(-x)) / 2, where e is the base of the natural logarithm.
How are hyperbolic functions related to real-life applications such as the curvature of electric wires?
-Hyperbolic functions describe the shape of a cable hanging between two points, which is based on the hyperbolic cosine function. This is because the curve that the wire takes is the path of least resistance, which is mathematically described by hyperbolic functions, specifically the hyperbolic cosine.
What are the main differences between the Pythagorean identities of trigonometric and hyperbolic functions?
-The Pythagorean identity for trigonometric functions is sin^2(x) + cos^2(x) = 1, while for hyperbolic functions, the identity is cosh^2(x) - sinh^2(x) = 1. The main difference is the use of subtraction in the hyperbolic identity instead of addition in the trigonometric identity.
How does the proof of the double angle formula for hyperbolic functions relate to the trigonometric version?
-The double angle formula for hyperbolic functions, cosh(2x) = 2cosh(x)cosh(x), is similar to the trigonometric version, cos(2x) = 2cos(x)cos(x). The proof involves using the definitions of hyperbolic functions and algebraic manipulation, similar to the trigonometric proof, but with hyperbolic functions' properties.
What is the derivative of the hyperbolic cosine function?
-The derivative of the hyperbolic cosine function, cosh(x), with respect to x is sinh(x), which is defined as (e^x - e^(-x)) / 2.
How do the derivatives of hyperbolic functions relate to their integrals?
-The derivatives of hyperbolic functions can be used to find their integrals through the process of integration by parts or substitution, similar to the process used with trigonometric functions. The integral of a hyperbolic function often results in another hyperbolic function or a combination of hyperbolic and exponential functions.
What are the main properties of hyperbolic functions that make them useful in engineering?
-Hyperbolic functions are useful in engineering because they model certain physical phenomena that involve exponential growth or decay, such as the distribution of heat in a conducting medium or the shape of a cable suspended between two points.
How does the concept of odd and even functions relate to hyperbolic functions?
-Hyperbolic functions, like trigonometric functions, can be classified as odd or even. For example, the hyperbolic sine function (sinh(x)) is an odd function because sinh(-x) = -sinh(x), while the hyperbolic cosine function (cosh(x)) is an even function because cosh(-x) = cosh(x).
What is the relationship between the hyperbolic tangent function and the hyperbolic secant function in terms of derivatives?
-The derivative of the hyperbolic tangent function, tanh(x), is the hyperbolic secant function, sech(x), which is similar to the relationship between the trigonometric tangent and secant functions. This means that the derivative of tanh(x) with respect to x is sech(x) times the derivative of x, which is 1.
How can the properties of hyperbolic functions be used to solve real-world problems?
-The properties of hyperbolic functions, such as their derivatives and integrals, can be applied to solve problems in various fields, including physics, engineering, and economics, where exponential growth or decay is involved. For instance, they can be used to model population growth, the spread of diseases, or the behavior of certain materials under stress.
Outlines
📚 Introduction to Hyperbolic Functions
The speaker introduces the topic of hyperbolic functions, highlighting their similarities to trigonometric functions and their practical applications in real-life scenarios such as the curvature of electrical wires. The definitions of hyperbolic functions are provided, emphasizing the hyperbolic cosine and tangent, and their relationships to exponential functions. The speaker also discusses the importance of understanding these functions for engineering purposes.
🔍 Properties and Identities of Hyperbolic Functions
The discussion continues with the exploration of properties and identities of hyperbolic functions, drawing parallels to trigonometric identities. The speaker explains the odd and even nature of hyperbolic functions, using the hyperbolic cosine as an example. The Pythagorean identities for both trigonometric and hyperbolic functions are compared, highlighting the differences. The speaker also mentions that some identities will be familiar, while others will have slight variations.
🧠 Derivatives of Hyperbolic Functions
The speaker delves into the derivatives of hyperbolic functions, providing a step-by-step explanation of how to derive them using basic identities and definitions. The process of proving these derivatives is discussed, emphasizing the use of chain rules and other calculus techniques. The speaker also mentions that the derivatives of hyperbolic functions will be covered in more detail, with examples and proofs to follow.
📈 Derivative Proofs and Applications
The speaker provides a detailed proof of the derivative of the hyperbolic cosine function, using algebraic manipulation and the chain rule. The process of proving the derivative is explained, with the speaker emphasizing the importance of understanding the underlying concepts. The speaker also discusses the application of these derivatives in solving problems, and encourages the audience to practice and familiarize themselves with these new concepts.
🌐 Practical Applications and Further Discussion
The speaker emphasizes the practical applications of hyperbolic functions in real-life scenarios, such as the design of suspension bridges and the behavior of electric fields. The discussion then shifts to the derivatives and integrals of hyperbolic functions, with the speaker providing a table of these formulas for easy reference. The speaker encourages the audience to keep these formulas handy for future use in their studies.
📝 Derivative Examples and Chain Rule
The speaker provides examples of using the chain rule to find the derivatives of hyperbolic functions. The process is demonstrated with a specific example, showing how to apply the chain rule and how the derivatives of hyperbolic functions are similar to those of trigonometric functions. The speaker also discusses the importance of practice and familiarity with these concepts, and encourages the audience to work through the examples on their own.
🤔 Inverse Hyperbolic Functions and Logarithmic Forms
The speaker introduces inverse hyperbolic functions, explaining their notation and their relationship to logarithmic forms. The definitions of the inverse hyperbolic cosine, tangent, and secant are provided, and the speaker demonstrates how to derive these functions from their exponential counterparts. The process of deriving the inverse functions is shown, with the speaker using algebraic techniques and the quadratic formula to arrive at the final forms.
📊 Derivatives of Inverse Hyperbolic Functions
The speaker discusses the derivatives of inverse hyperbolic functions, providing the formulas and explaining their derivation. The process of finding the derivative of the inverse hyperbolic cosine is detailed, with the speaker using the chain rule and logarithmic properties. The speaker also mentions that the derivatives of other inverse hyperbolic functions can be found using similar techniques, and provides the formulas for these derivatives.
🎓 Summary and Lightening the Load
The speaker summarizes the key points covered in the discussion on hyperbolic functions, including their properties, identities, derivatives, and inverse functions. The speaker emphasizes the importance of understanding these concepts and practicing their application. The discussion then concludes with the speaker indicating that the next section will not cover integrals, aiming to keep the content light and manageable for the audience.
Mindmap
Keywords
💡Hyperbolic functions
💡Inverse hyperbolic functions
💡Derivatives
💡Integrals
💡Chain rule
💡Logarithms
💡Trigonometric functions
💡Exponential functions
💡Algebraic manipulation
💡Quadratic formula
Highlights
The introduction to hyperbolic functions and their similarities with trigonometric functions.
Definition of hyperbolic cosine (cosh) and its relationship with the exponential function.
Explanation of how hyperbolic functions are used in real-life engineering, such as the curvature of electrical wires.
The definition and properties of hyperbolic tangent (tanh) and its relation to the hyperbolic cosine.
Discussion of the identities of hyperbolic functions and their parallels with trigonometric identities.
Proof of the identity involving the double angle formula for hyperbolic cosine.
Introduction to the derivatives of hyperbolic functions and their relation to the original functions.
Explanation of the chain rule and its application in finding the derivatives of hyperbolic functions.
Presentation of the integrals of hyperbolic functions and their connection to the exponential function.
Practice of solving problems involving hyperbolic functions through the use of derivatives and integrals.
The concept of inverse hyperbolic functions and their existence due to the one-to-one nature of hyperbolic functions.
Expression of inverse hyperbolic functions as logarithms, drawing a connection with the inverse relationship between exponential and logarithmic functions.
Proof of the formula for the inverse hyperbolic cosine function using algebraic manipulation and the quadratic formula.
Derivation of the formula for the derivative of the inverse hyperbolic cosine function.
Overview of the derivatives for other inverse hyperbolic functions and their similarities to the derivative of the inverse hyperbolic cosine.
Illustration of the product rule in the context of a function involving the inverse hyperbolic secant function.
Emphasis on the importance of the chain rule in the differentiation process of hyperbolic and inverse hyperbolic functions.
Transcripts
Browse More Related Video
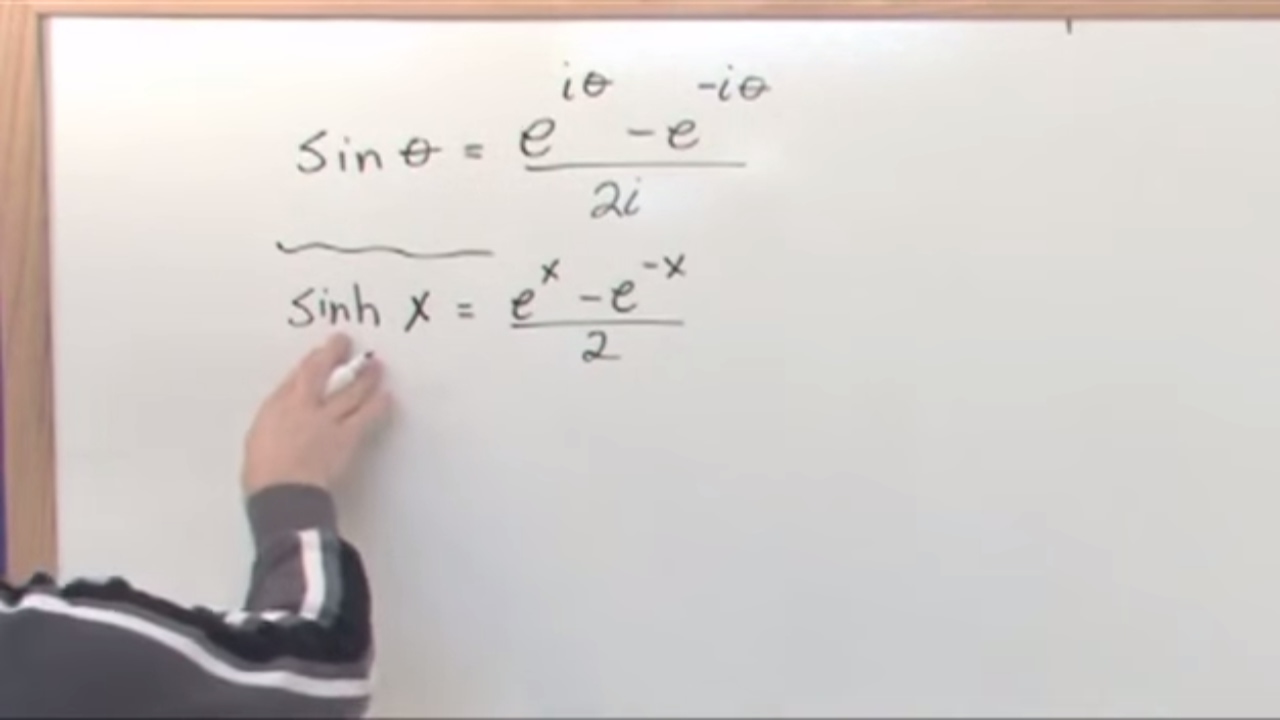
Lesson 3 - Hyperbolic Functions (Calculus 2 Tutor)

Lesson 4 - Inverse Hyperbolic Functions (Calculus 2 Tutor)
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses

Derivatives of Trig Functions - Calculus | MCV4U
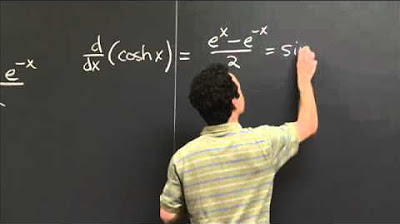
Hyperbolic trig functions | MIT 18.01SC Single Variable Calculus, Fall 2010

DERIVATIVES that keep getting HARDER 🤯 | jensenmath.ca
5.0 / 5 (0 votes)
Thanks for rating: