Related rates intro | Applications of derivatives | AP Calculus AB | Khan Academy
TLDRThe video script explains the concept of how the area of a ripple formed by a rock dropped into water grows over time. It uses the principles of geometry and calculus to derive the rate of change of the area with respect to time. The area of the circle is given by pi times the radius squared, and with the radius increasing at 1 cm/s, the final calculation shows that the area is increasing at a rate of 6 pi square centimeters per second.
Takeaways
- 🌊 A ripple forms a circle when a rock is dropped into water, moving radially outwards from the point of impact.
- 📐 The radius of the ripple increases over time, in this case, at a rate of 1 centimeter per second.
- 🔢 The area of a circle is calculated using the formula A = πr², where A is the area and r is the radius.
- 🚀 To find the rate of change of the area, we differentiate both sides of the area formula with respect to time.
- 📌 The derivative of the area with respect to time is represented as dA/dt, which will give us the rate of change of the area.
- 📝 Applying the chain rule is crucial for differentiating the area with respect to time, as r is a function of time (r(t)).
- 🌀 The derivative of r² with respect to r is 2r, but we must also multiply by the derivative of r with respect to time (dr/dt) to find dA/dt.
- 🎯 At the specific moment when r = 3 cm and dr/dt = 1 cm/s, the rate of change of the area (dA/dt) is 6π square centimeters per second.
- 📈 The rate of growth of the area is directly proportional to the square of the radius and the rate of change of the radius.
- 🌟 This mathematical analysis demonstrates the relationship between geometric shapes and their dynamic properties over time.
Q & A
What happens when a rock is dropped into a pool of water?
-When a rock is dropped into a pool of water, it creates a ripple that moves radially outwards from the point of impact.
How is the ripple described in the script?
-The ripple is described as a circle centered at the point where the rock initially hit the water, with its radius increasing at a rate of 1 centimeter per second.
What is the radius of the ripple at the moment mentioned in the script?
-At the moment mentioned in the script, the radius of the ripple is 3 centimeters.
What is the relationship between the area of a circle and its radius?
-The area of a circle is equal to pi times the radius squared (A = πr^2).
How is the rate of change of the circle's area with respect to time calculated?
-The rate of change of the circle's area with respect to time is calculated by taking the derivative of the area with respect to time, applying the chain rule, and using the formula 2πr * dr/dt.
What is the value of dr/dt in the script's scenario?
-In the script's scenario, the value of dr/dt is 1 centimeter per second.
What is the unit of measurement for the rate of change of the area?
-The unit of measurement for the rate of change of the area is square centimeters per second (cm^2/s).
What is the rate at which the area of the ripple is growing at the specific moment described in the script?
-At the specific moment described in the script, the area of the ripple is growing at a rate of 6π square centimeters per second.
How does the chain rule apply to this problem?
-The chain rule applies to this problem when taking the derivative of the area with respect to time, as it involves differentiating a composite function, specifically the area in terms of the radius as a function of time.
What is the final expression used to calculate the rate of change of the area?
-The final expression used to calculate the rate of change of the area is dA/dt = 2πr * dr/dt.
Outlines
🌊 Ripple Formation and Growth
This paragraph introduces a scenario where a rock is dropped into a pool of water, creating a ripple that propagates outward. The ripple is described as a circle with a radius that starts at 3 centimeters and increases by 1 centimeter per second. The main focus is on understanding the rate at which the area of this ripple circle is growing. The speaker sets up the problem by explaining the known conditions and hints at using mathematical concepts to find the solution.
📐 Calculating the Growth Rate of the Circle's Area
In this paragraph, the speaker delves into the mathematical process of determining the rate at which the area of the ripple circle is increasing. The explanation involves the use of the area formula for a circle (A = πr^2), differentiation with respect to time, and application of the chain rule. The speaker calculates the derivative of the area with respect to time, which is found to be equal to 2πr(dr/dt). By substituting the given values of r = 3 cm and dr/dt = 1 cm/s, the speaker concludes that the rate of change of the area (da/dt) is 6π square centimeters per second at that particular moment.
Mindmap
Keywords
💡pool of water
💡ripple
💡radially outward
💡circle
💡radius
💡area
💡rate of change
💡derivative
💡chain rule
💡pi (π)
💡function of time
Highlights
The scenario involves a ripple forming radially outwards after a rock is dropped into a pool of water.
The ripple is modeled as a circle with a radius that starts at 3 centimeters and increases at a rate of 1 centimeter per second.
The goal is to determine the rate at which the area of the circle (ripple) is growing over time.
The area of a circle is given by the formula A = πr^2, where r is the radius.
To find the rate of change of the area, the derivative of the area with respect to time is taken, resulting in dA/dt = 2πr(dr/dt).
The chain rule is applied to relate the rate of change of the area to the rate of change of the radius.
The derivative of the area with respect to time is expressed as dA/dt = 2πr * dr/dt.
At the given moment, the radius r is 3 cm and the rate of change of the radius dr/dt is 1 cm/s.
By substituting the known values, the rate of change of the area is calculated to be 6π cm^2/s.
The problem demonstrates the application of calculus in understanding the dynamics of physical phenomena.
The solution process illustrates the importance of understanding the relationship between different variables and their rates of change.
The use of the chain rule in this context emphasizes its utility in solving problems involving composite functions.
The example serves as an excellent demonstration of how mathematical concepts can be applied to real-world situations.
The problem-solving approach showcases the step-by-step method of applying calculus to derive the rate of change of an area.
The explanation highlights the significance of the initial conditions in determining the mathematical model of the situation.
The final answer, 6π cm^2/s, represents the rate at which the ripple's area is expanding at that particular moment.
The transcript effectively communicates the process of solving a practical problem using fundamental calculus concepts.
Transcripts
Browse More Related Video
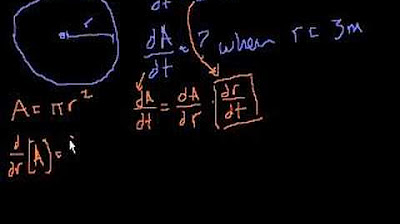
Rates-of-change (part 2)

How to solve a changing area of circle with related rates

AP CALCULUS AB 2022 Exam Full Solution FRQ#4d

Related rates of volume and area of a cube

2011 Calculus BC free response #3 (b & c) | AP Calculus BC | Khan Academy

Related rates: water pouring into a cone | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: