Justification with the intermediate value theorem: table | AP Calculus AB | Khan Academy
TLDRThe video script discusses the application of the intermediate value theorem to determine the existence of solutions for a continuous function within specified intervals. It illustrates the concept using a function f(x) with given values at certain points. The theorem is used to justify that there must be a value 'c' between 2 and 4 where f(c) equals zero, as zero lies between f(2) and f(4). However, it clarifies that the theorem cannot be applied to find a solution for f(x) = 0 between x=4 and x=6, as zero is not within the range of f(4) and f(6).
Takeaways
- 📈 The Intermediate Value Theorem (IVT) is applicable to continuous functions and helps determine if a function has a solution over a specified interval.
- 🔍 The IVT cannot be used to find a solution for f(x) = 0 between x = 4 and x = 6 since 0 is not between f(4) and f(6).
- 📌 The continuity of a function allows us to draw a graph without lifting the pencil, indicating that the function takes on all values between given points.
- 🤔 To apply the IVT, one must choose a closed interval and check if the desired value lies between the function values at the interval's endpoints.
- 🔗 The IVT ensures that within a continuous function over a closed interval, the function will take on every value between the function values at the endpoints.
- 👉 For the interval x = 2 to x = 4, since f(2) is negative and f(4) is positive, and the function is continuous, there must exist a c such that f(c) = 0.
- 📊 The visual representation of the function's values helps in understanding the application of the IVT and identifying where the function crosses the x-axis.
- 🌐 The concept of continuity is crucial for the IVT and is assumed for the function unless otherwise specified.
- 🎯 The IVT is a powerful tool in calculus that provides a guarantee of existence of roots for continuous functions within certain intervals.
- 📝 The proof of the existence of a root using the IVT does not provide the exact value or location of the root, only its existence.
Q & A
What is the Intermediate Value Theorem and how does it relate to the given function f?
-The Intermediate Value Theorem states that if a function f is continuous on a closed interval [a, b], then for any value k between f(a) and f(b), there exists at least one c in the interval [a, b] such that f(c) = k. In the context of the given function f, this theorem helps determine if there exists a solution to the equation f(x) = 0 within specified intervals.
Why can't we apply the Intermediate Value Theorem to find a solution for f(x) = 0 in the interval [4, 6]?
-We cannot apply the Intermediate Value Theorem to the interval [4, 6] to find a solution for f(x) = 0 because zero is not between the function values at the endpoints of the interval, which are f(4) = 3 and f(6) = 7. The theorem requires that the value we are looking for (in this case, zero) must lie between the function values at the interval's boundaries.
How does the continuity of a function affect the application of the Intermediate Value Theorem?
-The continuity of a function is a prerequisite for applying the Intermediate Value Theorem. A function must be continuous on the interval in question to ensure that it takes on every value between its function values at the endpoints of the interval. Without continuity, the theorem does not hold, and we cannot guarantee that the function will take on a specific value within the interval.
What is the significance of the point where f(x) = 0 in the context of the Intermediate Value Theorem?
-The significance of the point where f(x) = 0 is that it represents a solution to the equation f(x) = 0. According to the Intermediate Value Theorem, if such a point exists within a given interval and the function is continuous on that interval, then there must be at least one value c in that interval for which f(c) = 0.
How does the value of f(x) at the endpoints of an interval affect the application of the Intermediate Value Theorem?
-The values of f(x) at the endpoints of an interval are crucial for the Intermediate Value Theorem because they help determine whether a specific value lies between them. The theorem states that if a function is continuous on a closed interval [a, b], then it will take on every value between f(a) and f(b). Therefore, if the value we are looking for lies between these two endpoint values, the theorem can be applied.
What is the closed interval [2, 4] in the context of the script, and why is it important?
-The closed interval [2, 4] refers to the range of x-values from 2 to 4, inclusive. It is important because it is the interval over which we are trying to find a solution to f(x) = 0 using the Intermediate Value Theorem. The theorem can be applied here because the function is continuous on this interval, and zero lies between the function values at the endpoints.
What does the function value f(2) = -2 indicate for the interval [2, 4]?
-The function value f(2) = -2 indicates that at the left endpoint of the interval [2, 4], the function takes on a negative value. This, along with the value of the function at the right endpoint (f(4) = 3), helps determine that zero lies between these two values, allowing us to apply the Intermediate Value Theorem.
How does the visual representation of the function in the script aid in understanding the Intermediate Value Theorem?
-The visual representation of the function helps to intuitively understand the Intermediate Value Theorem by showing how the function values vary between the endpoints of an interval. By visualizing the function connecting the given points without lifting the pencil, we can see that the function must cross every value between the endpoint values at least once, including zero in this case, which supports the theorem's application.
What is the role of the function's continuity in ensuring that the Intermediate Value Theorem can be used?
-The continuity of the function is essential because it ensures that the function does not have any gaps, jumps, or breaks within the interval. This property allows us to confidently use the Intermediate Value Theorem, knowing that the function will take on every value between the function values at the endpoints of the interval without missing any values.
How does the Intermediate Value Theorem help in finding the solution for f(x) = 0 in the interval [2, 4]?
-The Intermediate Value Theorem helps in finding the solution for f(x) = 0 in the interval [2, 4] by confirming that since the function is continuous on this interval and zero lies between the function values at the endpoints (f(2) = -2 and f(4) = 3), there must exist at least one value c in the interval [2, 4] such that f(c) = 0.
What is the conclusion drawn from the application of the Intermediate Value Theorem to the interval [2, 4]?
-The conclusion drawn from the application of the Intermediate Value Theorem to the interval [2, 4] is that there exists a value c within this interval for which f(c) = 0. This means that the equation f(x) = 0 has at least one solution in the interval [2, 4].
Outlines
📚 Application of the Intermediate Value Theorem
This paragraph discusses the application of the Intermediate Value Theorem to determine if a continuous function has a solution within a specified interval. The instructor first introduces the theorem and its relevance to the given problem, which is to find if the equation f(x) = 0 has a solution for 4 ≤ x ≤ 6. The explanation is aided by a visual representation, plotting the given values of the function on a graph. The instructor emphasizes the continuity of the function, which allows for the connection of the plotted points without lifting the pencil. However, it is concluded that the Intermediate Value Theorem cannot be applied here because zero is not between f(4) and f(6). The theorem would guarantee the existence of a solution if the value was between the function values at the endpoints of the interval. The paragraph then transitions to a new problem, asking if there is a value c such that f(c) = 0 for 2 ≤ c ≤ 4. The continuity of the function is reiterated, and by examining the function values at the endpoints of this new interval, the instructor confirms that zero lies between f(2) and f(4), thus applying the theorem and asserting the existence of such a value c.
🔍 Visualizing the Existence of a Zero within an Interval
This paragraph further elaborates on the previous discussion by visually demonstrating the existence of a zero for the continuous function within the interval [2, 4]. The instructor uses the graph to illustrate that moving from one point to another without lifting the pen, one must cross every value between f(2) and f(4) at least once. This visual representation reinforces the mathematical concept that due to the continuity and the value zero being between f(2) and f(4), there must exist a point c in the interval where f(c) equals zero. The explanation aims to clarify the somewhat abstract concept of the Intermediate Value Theorem by providing an intuitive understanding of how the theorem can be visualized and applied in practical scenarios.
Mindmap
Keywords
💡Intermediate Value Theorem
💡Continuous Function
💡Closed Interval
💡Function Values
💡Solution
💡Graph
💡Visualization
💡Endpoints
💡Zero
💡Fluctuations
💡Crossing the X-axis
Highlights
The Intermediate Value Theorem is discussed in the context of a continuous function f.
The theorem is applied to determine if there's a solution where f(x) = 0 for x between 4 and 6.
A visual representation of the function's values at specific points is provided to aid understanding.
The function f(x) is continuous, which means it can be drawn without lifting the pencil from the paper.
The Intermediate Value Theorem states that a continuous function will take on every value between f(4) and f(6) over a closed interval.
Zero is not between f(4) and f(6), so the theorem cannot be used to find a solution for f(x) = 0 in the interval 4 to 6.
The problem is rephrased to find a value c such that f(c) = 0 with 2 ≤ c ≤ 4.
Given that f is continuous, the theorem can be applied to the interval from 2 to 4.
The function values at the endpoints of the interval are f(2) = -2 and f(4) = 3.
Zero lies between f(2) and f(4), which means the function must cross the x-axis within the interval.
The Intermediate Value Theorem confirms the existence of a value c in the interval [2, 4] where f(c) = 0.
The theorem's application ensures that the function crosses every value between f(2) and f(4) at least once.
The discussion provides an intuitive understanding of the theorem's implications for continuous functions.
The mathematical concept is made more accessible through visual representation and step-by-step explanation.
The video pauses are used effectively to engage the viewer in active problem-solving.
The transcript serves as a comprehensive guide for those learning about the Intermediate Value Theorem and its applications.
Transcripts
Browse More Related Video

Using the Intermediate Value Theorem Examples

Justification with the intermediate value theorem: equation | AP Calculus AB | Khan Academy
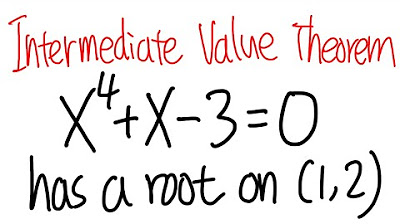
Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval
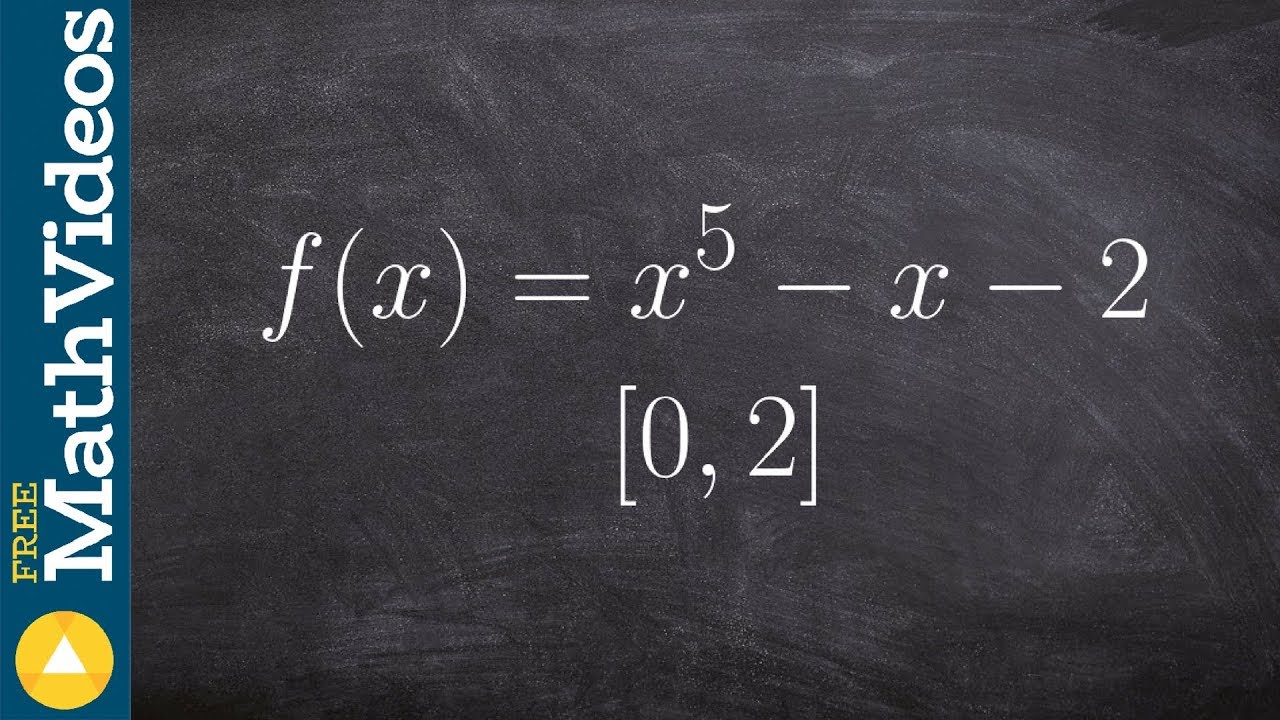
How to show that a solution exists to a functions using IVT

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy
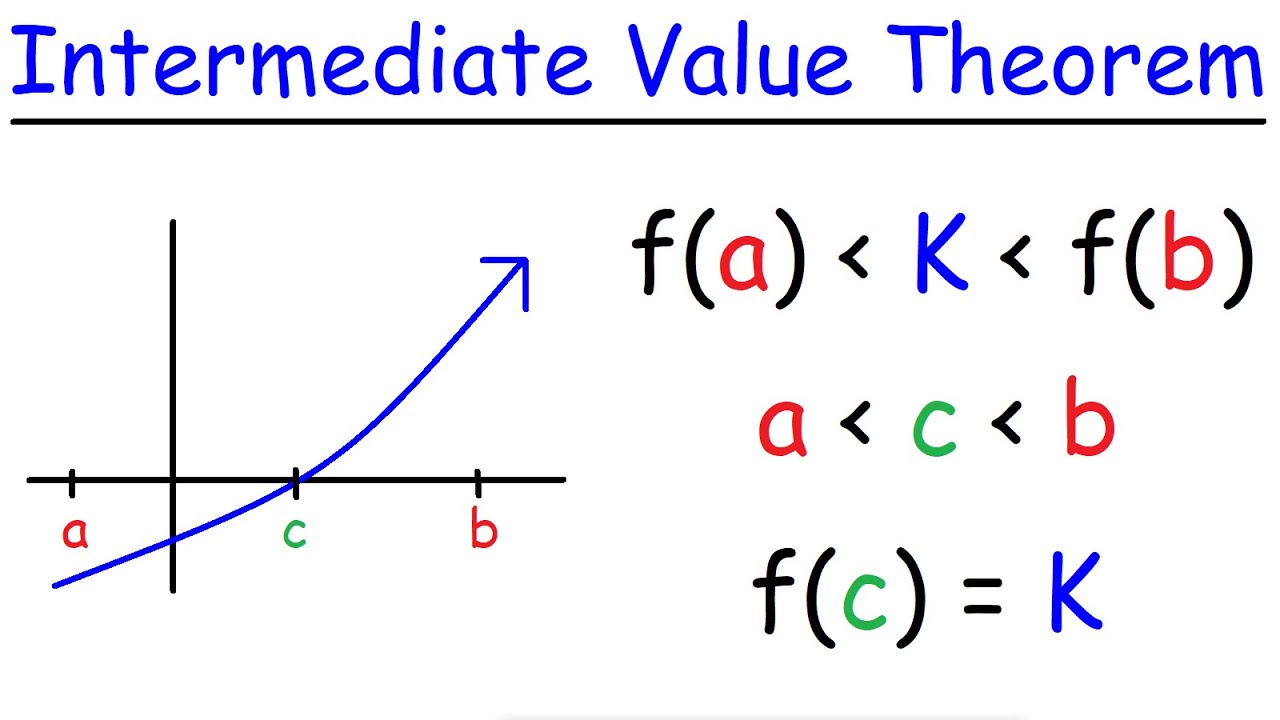
Intermediate Value Theorem
5.0 / 5 (0 votes)
Thanks for rating: