High School Physics - Newton's 2nd Law
TLDRIn this informative talk, Mr. Fullerton explores Newton's second law of motion, highlighting its significance in classical physics and various applications. He explains the relationship between acceleration, force, and mass, and differentiates between mass and weight. Through examples and demonstrations, he illustrates how to apply the law to solve problems, emphasizing the concept of net force and static equilibrium. The discussion also touches on how weight varies across different gravitational fields, using hypothetical scenarios with an astronaut and an alien to clarify the concept.
Takeaways
- 📜 Newton's Second Law of Motion is fundamental to understanding classical physics and has wide applications in various fields.
- 🔗 The relationship between acceleration, force, and mass is central to Newton's Second Law, which states that the acceleration of an object is directly proportional to the net force applied and inversely proportional to its mass.
- 🎯 Mathematically, Newton's Second Law is expressed as F_net = m * a, where F_net is the net force, m is the mass, and a is the acceleration.
- 🚀 The direction of an object's acceleration is aligned with the direction of the net force acting upon it.
- ⚖️ Mass and weight are different; mass is a measure of an object's inertia and remains constant, while weight is the force of gravity on an object and can vary depending on the gravitational field.
- 🤼♀️ When multiple forces act on an object, the net force is the overall force after considering all the individual forces and their directions.
- 📊 To apply Newton's Second Law, start by drawing a Freebody diagram to visualize all forces acting on the object and break down forces into components along the X and Y axes if necessary.
- 🔢 Use the law to calculate unknowns such as acceleration, force, or mass by setting up equations based on the net force in each direction and solving them.
- 🌌 Newton's First Law is a subset of the Second Law, describing the motion of an object when there is no net force acting upon it (net force equals zero).
- 🛠️ Practical examples, such as pushing a tractor-trailer versus a matchbox car, illustrate the inverse relationship between mass and acceleration when a constant force is applied.
- 🔄 The concept of static equilibrium is when all forces acting on an object are balanced, resulting in no acceleration, and an object remains at rest or continues moving at a constant velocity in a straight line.
Q & A
What is Newton's second law of motion?
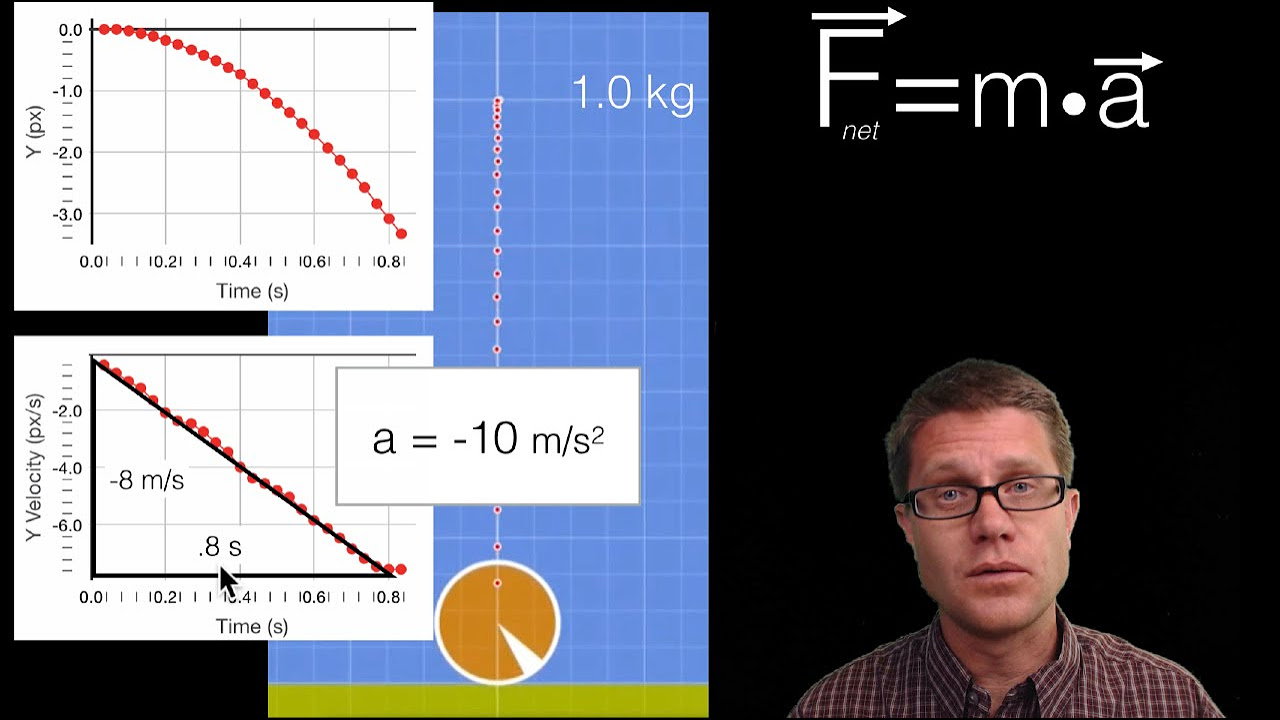
-Newton's second law of motion states that the acceleration of an object is in the direction of and directly proportional to the net force applied and inversely proportional to the object's mass. Mathematically, it can be expressed as F_net = m * a, where F_net is the net force, m is the mass, and a is the acceleration.
How is Newton's second law different from Newton's first law?
-Newton's first law, also known as the law of inertia, states that an object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity unless acted upon by a net force. Newton's second law explains what happens when a net force is applied: it causes an object to accelerate in the direction of the force. So, Newton's first law is a specific case of Newton's second law when the net force is zero.
What does net force mean in the context of Newton's second law?
-Net force refers to the overall force acting on an object after considering all the individual forces (vectors) acting on it. It is the resultant force that takes into account both the magnitude and direction of all forces. For example, if two equal and opposite forces act on an object, the net force is zero, and there will be no acceleration according to Newton's second law.
How does mass differ from weight?
-Mass is a measure of the amount of matter in an object and is an intrinsic property that does not change regardless of the object's location. Weight, on the other hand, is the force of gravity acting on an object and can vary depending on the gravitational field the object is subjected to. For instance, an astronaut's mass remains the same on Earth and on the Moon, but their weight changes due to the difference in gravitational field strength.
What is a Freebody diagram, and how is it used in applying Newton's second law?
-A Freebody diagram is a graphical representation that shows all the forces acting on an object. It helps in visualizing and analyzing the situation by breaking down the forces into components along the X, Y, and Z axes if necessary. When applying Newton's second law, a Freebody diagram aids in writing expressions for the net force in each direction and then setting up the equation F_net = m * a to solve for the unknowns, such as acceleration or force.
How can you determine the mass of an object using Newton's second law if you know the acceleration and the net force?
-If you know the acceleration (a) and the net force (F_net) acting on an object, you can determine the mass (m) by rearranging the formula of Newton's second law: m = F_net / a. By substituting the known values of net force and acceleration, you can calculate the mass of the object.
What is static equilibrium, and how does it relate to Newton's second law?
-Static equilibrium occurs when there is no net force acting on an object, meaning all the forces are balanced. The object does not accelerate. This situation is related to Newton's second law, which states that an object will not accelerate unless acted upon by a net force. In static equilibrium, the net force is zero, so according to Newton's second law, the acceleration of the object is also zero.
What is an equilibrant vector, and how is it used in force analysis?
-An equilibrant vector is a hypothetical single force that, when added to a system of unbalanced forces, brings the system into static equilibrium. It is used in force analysis to determine the additional force required to balance a system. For example, if you have a net force of 20 Newtons to the northeast, an equilibrant vector of 20 Newtons to the southwest would be needed to achieve equilibrium.
How can you find the gravitational field strength on another planet if you know the weight and mass of an object or alien on Earth and on that planet?
-To find the gravitational field strength (G) on another planet, you can use the formula for weight on Earth (weight = m * g_earth) and the weight on the other planet (weight_planet = m * G_planet). By setting up a ratio of the weights and solving for G_planet, you can find the gravitational field strength on the other planet. For example, if an astronaut has a weight of 1000 Newtons on Earth and 612 Newtons on Planet X, the gravitational field strength on Planet X is G_planet = weight_planet / mass.
What happens to the acceleration of an object when the net force acting on it changes?
-According to Newton's second law, when the net force acting on an object changes, the acceleration of the object also changes proportionally. If the net force increases, the acceleration increases, and if the net force decreases, the acceleration decreases. The direction of the acceleration also changes to align with the direction of the net force.
How can you calculate the net force acting on an object when multiple forces act concurrently in different directions?
-To calculate the net force when multiple forces act concurrently in different directions, you need to break down each force into its components along the coordinate axes (usually X and Y). Then, you sum up the components in each direction, taking into account their signs based on the chosen positive direction. Finally, you can find the net force by considering the resultant of all these components, often using the Pythagorean theorem for vector addition.
Outlines
📚 Introduction to Newton's Second Law
This paragraph introduces Newton's second law of motion, emphasizing its importance in understanding classical physics. Mr. Fullerton explains that the law describes the relationship between an object's acceleration, the net force applied to it, and its mass. The video aims to provide a brief overview and plans to cover more applications and subtleties in future videos. The discussion also touches on the difference between mass and weight, and the concept of static equilibrium.
🔍 Applying Newton's Second Law to Problems
In this paragraph, Mr. Fullerton delves into the application of Newton's second law to solve physical problems. He explains how to calculate net force and the resulting acceleration when forces are applied in different directions. The concept of net force is illustrated with a relatable example involving a tractor-trailer and a matchbox car. The paragraph also discusses Newton's first law as a special case of the second law and outlines the steps to solve problems using free body diagrams and net force equations.
🌠 Understanding Mass, Weight, and Static Equilibrium
This section clarifies the difference between mass and weight, and introduces the concept of static equilibrium. Mr. Fullerton explains that mass is a measure of an object's inertia and remains constant, while weight varies with the gravitational field. The example of an astronaut's weight on Earth and another planet illustrates this concept. The paragraph also discusses how to calculate the required force to bring an object into static equilibrium and provides a problem-solving approach using free body diagrams and net force equations.
🚫 Forces That Cannot Result in Equilibrium
The final paragraph addresses the conditions under which two concurrent forces cannot produce equilibrium. By examining the resultant force of two given forces, Mr. Fullerton explains that if the sum of these forces exceeds the magnitude required to balance the object, equilibrium cannot be achieved. The paragraph reinforces the importance of understanding the vector nature of forces and the conditions necessary for static equilibrium, emphasizing the need for precise problem analysis and force vector calculations.
Mindmap
Keywords
💡Newton's Second Law
💡Acceleration
💡Force
💡Mass
💡Weight
💡Freebody Diagram
💡Net Force
💡Static Equilibrium
💡Inertia
💡Kinematic Equations
💡Gravitational Field Strength
Highlights
Newton's second law of motion is one of the most important laws in classical physics.
The law is applicable in many different areas, not just physics.
The goal is to explain the relationship between acceleration, force, and mass.
Newton's second law states that the acceleration of an object is directly proportional to the net force applied and inversely proportional to its mass.
The mathematical expression of the law is F_net = m * a, where F_net is the net force, m is the mass, and a is the acceleration.
An object's mass affects its acceleration; larger mass results in less acceleration for the same force applied.
Net force is the overall force after considering all the individual forces acting on an object.
Newton's first law is a subset of Newton's second law, applicable when the net force is zero.
To apply Newton's second law, one should start by drawing a Freebody diagram to visualize all forces.
The net force equations are written for each direction on the axes, and then set equal to mass times acceleration (F_net = m * a).
An example is given where two equal and opposite forces acting on a cart result in no acceleration (net force is zero).
The concept of static equilibrium is introduced, where no net force acts on an object, and it remains at rest or continues in uniform motion.
Mass is the amount of matter in an object and is constant, while weight is the force of gravity on the object and can vary depending on the gravitational field.
An astronaut's weight changes depending on the gravitational field, but their mass remains the same.
The equilibrant is the force needed to balance an unbalanced force and bring an object into static equilibrium.
A force greater than the resultant of two forces cannot produce equilibrium with those two forces.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: