AP Physics Workbook 7.B Torque
TLDRThis video script discusses the concept of torque in physics, specifically within the context of a large rod balanced by various forces. It explains the calculation of torque, the importance of the lever arm and the angle of rotation, and how to determine the force applied at different points along the rod. The video also illustrates how the position of the force application affects the torque and provides practical examples, such as hanging a shopping bag from the crook of the elbow versus carrying it suspended from the hand, to demonstrate the principles of torque in everyday life.
Takeaways
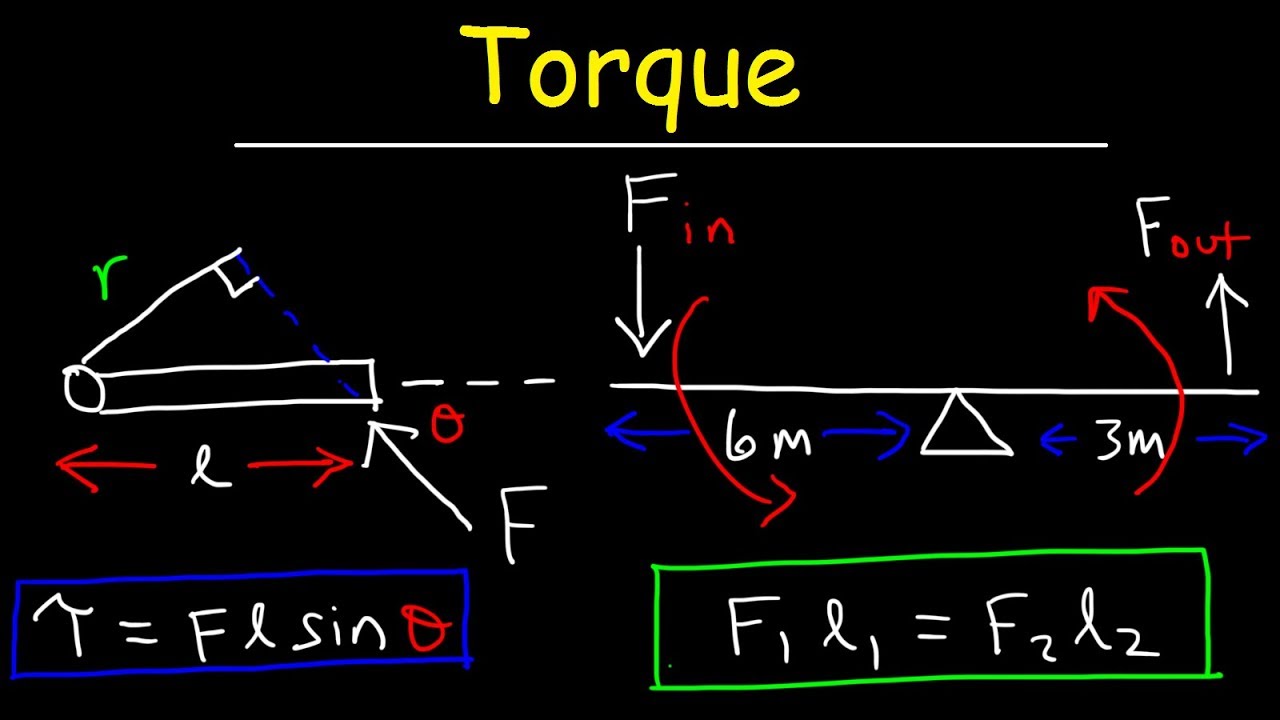
- 📚 Torque is a measure of how much force is applied at a distance from a pivot point, calculated as the product of force (F) and the radius (r).
- 🌟 The formula for torque can be expressed as τ = r * F * sin(θ), where θ is the angle between the force vector and the radius vector.
- ⚖️ When an object is in equilibrium, the sum of the external torques (clockwise and counterclockwise) must be equal to zero.
- 🔩 In the given scenario, a large rod of length L and mass M is supported at the left end and can rotate around a frictionless pivot.
- 📏 The rod is marked at 1/2 meter intervals, and the torque produced by the weight of the rod at each mark can be calculated using the mass, gravity, and the distance from the pivot.
- 🔢 For the example with M=1 kg and g=10 m/s², the force applied at a distance of 0.5 meters from the pivot results in a torque of 5 Nm (calculated as 0.5 * 1 * 10 / 2).
- 📈 The torques produced by the weight of the rod at different intervals (0.5, 1, 1.5, and 2 meters) can be ranked from highest to lowest based on their magnitudes.
- 🔄 The direction of the torque (clockwise or counterclockwise) is important and depends on the orientation of the force relative to the pivot point.
- 🤔 When hanging a shopping bag, it is easier to carry it from the crook of the elbow rather than suspending it from a hand with the arm at 90 degrees because the radius (distance from the pivot) is smaller, resulting in less torque and strain on the arm.
- 📝 It is crucial to consider all forces acting on a system, including the force of gravity, the force applied, and the reaction force from the pivot, to accurately calculate torques.
- 🎯 Understanding and applying the concept of torque is essential for solving problems in physics involving rotational equilibrium and dynamics.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the concept of torque and its application in the context of physics, specifically focusing on the scenario of a large rod with negligible mass supported at one end and subjected to various forces.
How is torque defined in the context of the video?
-In the video, torque is defined as the force applied to a perpendicular to the radius, where the radius is the lever arm, and the force is the magnitude of the force applied. Torque can also be expressed as the product of the force (F), the radius (R), and the sine of the angle of rotation (theta), represented as RF sine theta.
What is the significance of the angle of rotation in calculating torque?
-The angle of rotation, or theta, is significant in calculating torque because it determines the effective distance from the axis of rotation to the point where the force is applied. The sine of this angle is multiplied by the force and the radius to give the torque, indicating that torque is maximum when the force is applied perpendicular to the lever arm (i.e., when theta is 90 degrees).
How does the equilibrium of an object relate to torque?
-In the context of the video, when an object is in equilibrium, the sum of the external torques acting on it must be equal to zero. This means that the clockwise torques must balance the counterclockwise torques for the object to remain at rest.
What is the role of the radius in calculating torque?
-The radius, or lever arm, plays a crucial role in calculating torque. It represents the distance from the axis of rotation to the point where the force is applied. The torque is directly proportional to the radius, meaning that as the radius increases, the torque also increases, assuming the force remains constant.
How does the mass and length of the rod affect the torque calculation?
-In the given scenario, the mass (M) of the rod is taken into account when calculating the force of gravity (mg) acting on the rod. The length of the rod (L) is not directly used in the torque calculation for this specific problem, as the focus is on the points marked at 1/2 meter intervals from the supported end.
What is the purpose of the frictionless pen in the scenario described?
-The frictionless pen is used to support the left end of the rod and allows it to rotate freely around this point. This setup enables the study of torque and rotational equilibrium without the complicating factor of frictional forces.
What is the significance of marking the rod at 1/2 meter intervals?
-Marking the rod at 1/2 meter intervals is done to establish specific points where the torque calculations will be performed. These marks help in determining the radius (distance from the axis of rotation) for each point and thus calculating the torque at those points.
How does the force applied at different points along the rod affect the torque?
-The force applied at different points along the rod affects the torque by changing the radius (distance from the axis of rotation) at which the force is applied. A larger radius results in a greater torque, assuming the force remains constant. This is because torque is the product of the force, the radius, and the sine of the angle of rotation.
What is the practical application of understanding torque in everyday scenarios?
-Understanding torque is important in many everyday scenarios, such as opening a door, using tools, or even carrying a shopping bag. By understanding how the position of the applied force affects the torque, one can optimize the effort required to perform tasks, reduce strain on muscles, and improve mechanical efficiency.
Why is it easier to hang a shopping bag from the crook of your elbow rather than carrying it suspended from your hand with your arm at a 90-degree angle?
-Hanging a shopping bag from the crook of your elbow is easier because the radius (distance from the pivot point) is smaller, resulting in less torque and therefore less force required to hold the bag in equilibrium. When carrying the bag from your hand with your arm at a 90-degree angle, the radius is longer, which increases the torque and the force needed to hold the bag up, causing more strain on your arm.
Outlines
📚 Introduction to Torque and Rotations
This paragraph introduces the concept of torque and rotations in the context of AP Physics. It sets up a scenario involving a large rod of length L and mass M, supported at the left end and free to rotate about a frictionless pin. The rod is subjected to a vertical force and is at rest, marked at half-meter intervals. The key points discussed include defining torque, the lever arm concept, and the relationship between force, radius, and torque (R * F = M * g). The paragraph emphasizes the importance of understanding how torque is calculated and its role in equilibrium, where the sum of external torques must equal zero.
🔄 Calculating Torque with Examples
This paragraph delves into the process of calculating torque with specific examples. It explains how to determine the torque when forces are applied at different points along the rod. The paragraph clarifies the concept of the lever arm and its impact on torque calculation. It also discusses the relationship between clockwise and counterclockwise torques and their roles in maintaining equilibrium. The examples provided illustrate how to calculate the force applied at various points on the rod, using the formula R * F = M * g, and how to solve for unknown forces based on given values of mass, gravity, and radius.
💡 Understanding Torque at Equilibrium
This paragraph focuses on the application of torque concepts in a practical scenario, emphasizing the conditions for equilibrium. It uses a diagram to illustrate the forces acting on a box and a rod system, highlighting the importance of considering all forces, including those acting on the pin. The paragraph explains how to calculate the torque produced by gravity and the force applied, and how these torques must be balanced to maintain equilibrium. It also introduces the concept of ranking torques based on their values and provides a step-by-step explanation of the reasoning behind the calculations. The paragraph concludes with a real-world application, explaining why it's easier to hang a shopping bag from the crook of the elbow rather than carrying it suspended from the hand, due to the difference in the radius and the resulting torque.
Mindmap
Keywords
💡Torque
💡Rotation
💡Equilibrium
💡Lever Arm
💡Force
💡Mass
💡Gravity
💡Frictionless Pen
💡Radius
💡Angle of Rotation
💡Worked Example
Highlights
Introduction to the concept of torque in the context of AP Physics.
Explanation of torque as a force applied perpendicular to the radius and its relationship with the angle of rotation.
Definition of lever arm and its role in calculating torque.
Discussion on the equilibrium of torque, where external torque must be equal to zero.
Illustration of how torque is calculated using the formula RF sine theta.
Example problem involving a large rod with mass M and length L, supported by a frictionless pen.
Demonstration of ranking torque values based on the position of mass markers along the rod.
Explanation of how to calculate the force applied at different points along the rod.
Use of the lever arm and force of gravity to determine the torque produced by the mass at various intervals.
Clarification on how the radius and force interact to produce torque, with the formula R times F equals torque.
Solution to the example problem by setting the torque due to gravity equal to the torque applied by the finger.
Graphical representation of the forces acting on the box-rod system, emphasizing the importance of not ignoring the force of the pin.
Explanation of why it is easier to hang a shopping bag from the crook of the elbow rather than carrying it suspended from the hand at a 90-degree angle.
Discussion on the relationship between the radius, torque, and the force of tension, and how it affects the strain on the body.
Conclusion on the practical application of minimizing torque and strain by adjusting the position of the load relative to the pivot point.
Summary of the solutions for section 7 point B, including the definition and equations for torque at equilibrium.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: