Electromagnetic Spectrum Explained - Gamma X rays Microwaves Infrared Radio Waves UV Visble Light
TLDRThe video script offers an insightful overview of the electromagnetic spectrum, detailing the sequence from low-energy radio waves to high-energy cosmic radiation. It emphasizes the relationship between wavelength, frequency, and energy, explaining how these properties change across the spectrum. The script also introduces key equations, such as the speed of light equation and the Planck's constant equation, and provides step-by-step guides to calculating photon properties, including frequency, energy, and wavelength, using practical examples and conversions.
Takeaways
- 🌐 The electromagnetic spectrum includes radio waves, microwaves, infrared, visible light, ultraviolet rays, X-rays, gamma rays, and cosmic radiation.
- 📈 As you move right on the spectrum, energy and frequency increase, while wavelength decreases.
- 💡 A photon is a particle of light, and its energy is higher if it is further to the right on the spectrum.
- 🔵 A blue photon has more energy than a red photon due to its position on the spectrum.
- 🌡 Infrared has a higher frequency than microwaves because it is further to the right on the spectrum.
- 📏 X-rays have a longer wavelength than gamma rays as they are positioned further to the left on the spectrum.
- 🌟 The relationship between wavelength (λ), frequency (f), and energy (E) is such that shorter wavelength corresponds to higher energy and frequency.
- 🧬 Planck's constant (h) is used to calculate the energy of a photon using the equation E = h * f.
- 💥 The speed of light (c) in a vacuum is 3 * 10^8 meters per second and varies in different media due to the index of refraction.
- 📐 To convert nanometers to meters, multiply by 10^-9, and for energy, convert joules to electron volts using the factor 1.602 * 10^-19.
- 🔄 Given a photon's wavelength, energy, or frequency, one can calculate the other two using the equations relating these properties.
Q & A
What is the electromagnetic spectrum and how does energy vary across it?
-The electromagnetic spectrum is a range of all types of electromagnetic radiation, ordered by wavelength or frequency. As you move from radio waves to gamma rays in the spectrum, the energy of the photons increases. This is because higher frequency waves have shorter wavelengths and thus more energy, while lower frequency waves have longer wavelengths and less energy.
How does the frequency of electromagnetic waves relate to their wavelength?
-The frequency of electromagnetic waves is inversely proportional to their wavelength. As the wavelength increases, the frequency decreases, and vice versa. This relationship can be expressed by the equation: speed of light = wavelength × frequency, where the speed of light is a constant.
What is the speed of light and how does it change when light travels through different media?
-The speed of light in a vacuum is approximately 3 × 10^8 meters per second. However, when light travels through different media, such as water or glass, its speed changes based on the medium's refractive index. For example, in water with a refractive index of 1.33, the speed of light is about 2.26 × 10^8 meters per second.
How is the energy of a photon related to its frequency and wavelength?
-The energy of a photon is directly proportional to its frequency and inversely proportional to its wavelength. This relationship is described by the equation E = h × f, where E is the energy of the photon, h is Planck's constant, and f is the frequency. Alternatively, the energy can be calculated using E = (speed of light) / (wavelength), where the speed of light and wavelength are in meters.
What is Planck's constant and how is it used in the context of photon energy?
-Planck's constant is a fundamental physical constant that relates the energy of a photon to its frequency. Its value is approximately 6.626 × 10^-34 joules times seconds. It is used in the equation E = h × f to calculate the energy of a photon, where E is the energy, h is Planck's constant, and f is the frequency of the photon.
How can you convert the energy of a photon from joules to electron volts?
-The conversion factor between joules and electron volts is 1.602 × 10^-19 joules per electron volt. To convert the energy from joules to electron volts, you divide the energy value in joules by this conversion factor.
What is the wavelength of a red photon with a frequency of 4.286 × 10^14 hertz?
-Using the equation relating speed of light to wavelength and frequency (c = λ × f), the wavelength of a photon can be calculated as c / f. For a red photon with a frequency of 4.286 × 10^14 hertz, the wavelength is (3 × 10^8 m/s) / (4.286 × 10^14 Hz), which equals 700 nanometers.
What is the energy of a blue photon with a wavelength of 480 nanometers?
-Using the equation E = (speed of light) / (wavelength) and Planck's constant, the energy of a blue photon with a wavelength of 480 nanometers can be calculated as (3 × 10^8 m/s) / (480 × 10^-9 m) = 6.25 × 10^14 Hz. Then, using E = h × f, and substituting the frequency and Planck's constant, the energy is (6.626 × 10^-34 Js) × (6.25 × 10^14 Hz) = 4.14 × 10^-19 joules.
If a photon has an energy of 7 electron volts, what is its wavelength in nanometers?
-First, convert the energy from electron volts to joules using the conversion factor (1 eV = 1.602 × 10^-19 J). So, 7 eV = 7 × 1.602 × 10^-19 J = 1.1214 × 10^-18 J. Then, using the equation E = (speed of light) / (wavelength), and solving for the wavelength, we get: Wavelength = (speed of light) / (energy / Planck's constant) Wavelength = (3 × 10^8 m/s) / ((1.1214 × 10^-18 J) / (6.626 × 10^-34 Js)) This simplifies to a wavelength of approximately 177.3 nanometers.
What is the frequency of a photon with a wavelength of 600 nanometers?
-Using the equation relating speed of light to wavelength and frequency (c = λ × f), the frequency of a photon can be calculated as c / λ. For a wavelength of 600 nanometers, which is 600 × 10^-9 meters, the frequency f is (3 × 10^8 m/s) / (600 × 10^-9 m) = 5 × 10^14 Hz.
How does the refractive index of a medium affect the speed of light?
-The refractive index of a medium is a measure of how much the medium slows down the speed of light compared to a vacuum. The speed of light in a medium is given by c / n, where c is the speed of light in a vacuum and n is the refractive index of the medium. For example, if the refractive index is 1.5, the speed of light in that medium is (3 × 10^8 m/s) / 1.5.
What is the significance of understanding the relationship between wavelength, frequency, and energy in electromagnetic waves?
-Understanding the relationship between wavelength, frequency, and energy is crucial in various applications, including telecommunications, medical imaging, and astronomy. It helps in designing devices that use specific frequencies, interpreting data from spectroscopy, and understanding the behavior of light and other electromagnetic radiation in different environments.
Outlines
🌟 Introduction to the Electromagnetic Spectrum 🌟
This paragraph introduces the electromagnetic spectrum, explaining its order from lowest to highest energy. It starts with radio waves, the lowest energy with the longest wavelength, and progresses through microwaves, infrared, visible light (noting colors like red, orange, yellow, green, blue, violet), ultraviolet rays, x-rays, gamma rays, and cosmic radiation. The key concept is that as you move right on the spectrum, energy and frequency increase, while wavelength decreases. The paragraph also poses questions to engage the viewer, such as comparing the energy of a blue photon to a red photon, or the frequency of microwaves to infrared radiation, emphasizing that higher energy and frequency correspond to positions further right on the spectrum.
💧 Speed of Light and Index of Refraction 💧
The second paragraph delves into the speed of light and how it changes when traveling through different media. It explains that light travels slowest in a vacuum (3 x 10^8 meters per second) and varies in other materials based on their index of refraction. Water, for example, has an index of refraction of 1.33, slowing light to about 2.26 x 10^8 meters per second. Diamond, with a higher index of refraction (~2.4), slows light even more. The paragraph also introduces the relationship between wavelength, frequency, and energy, emphasizing that shorter wavelengths correspond to higher energy and frequency, and the equations that relate these variables.
🔧 Calculating Photon Energy and Frequency 🔧
This paragraph focuses on the practical calculations of photon energy and frequency. It explains how to calculate the frequency of a red photon with a wavelength of 700 nanometers using the speed of light and the wavelength. The process involves converting nanometers to meters and then dividing the speed of light by the wavelength to find the frequency in hertz. The energy of the photon is then calculated using Planck's constant and the frequency. The paragraph also introduces the concept of electron volts as a unit of energy and shows how to convert between joules and electron volts.
🔄 Converting Energy, Frequency, and Wavelength 🔄
The final paragraph covers advanced calculations involving energy, frequency, and wavelength. It demonstrates how to calculate the energy of a blue photon directly from its wavelength and how to work backwards from a given energy value to find the corresponding frequency and wavelength. The calculations involve using Planck's constant, the speed of light, and the relationships between energy, frequency, and wavelength. The paragraph concludes with a method for quickly converting from meters to nanometers by adjusting the exponent, highlighting the mathematical relationships fundamental to understanding the electromagnetic spectrum.
Mindmap
Keywords
💡Electromagnetic Spectrum
💡Wavelength
💡Frequency
💡Energy
💡Photon
💡Planck's Constant
💡Speed of Light
💡Index of Refraction
💡Red Photon
💡Blue Photon
💡Electron Volts
Highlights
The electromagnetic spectrum is introduced, starting with the lowest energy radio waves and progressing to the highest energy cosmic radiation.
The relationship between wavelength, frequency, and energy is explained, with energy increasing as you move to the right on the spectrum.
A comparison between blue and red photons reveals that blue photons have more energy due to their position on the spectrum.
The frequency of a type of electromagnetic wave increases as you move to the right on the spectrum, as demonstrated by infrared having a higher frequency than microwaves.
Wavelength increases as you move to the left on the spectrum, meaning radio waves have a longer wavelength than microwaves.
A practical example is given, showing how to calculate the frequency of a red photon with a wavelength of 700 nanometers.
The speed of light in a vacuum is a constant value used in calculations, which is 3 times 10 to the 8 meters per second.
The speed of light changes when it travels through different media, such as water or diamond, due to the material's index of refraction.
An equation relating the speed of light, wavelength, and frequency is provided, with the speed of light equal to lambda times frequency.
The energy of a photon is calculated using Planck's constant and the frequency, with the equation E equals h times f.
A step-by-step calculation shows how to find the energy of a red photon given its wavelength, resulting in 2.84 times 10 to the negative 19 joules.
The conversion between joules and electron volts is explained, with 1.602 times 10 to the negative 19 joules equal to one electron volt.
An example is provided to calculate the energy of a blue photon directly from its wavelength of 480 nanometers, resulting in 4.14 times 10 to the negative 19 joules.
A comprehensive problem is solved, working backwards from a photon's energy in electron volts to find its energy in joules, frequency, and wavelength.
The method for converting energy from electron volts to joules is demonstrated, multiplying the energy in electron volts by 1.6 times 10 to the negative 19.
The frequency of a photon is found by dividing the energy by Planck's constant, as shown in the calculation for a photon with 7 electron volts of energy.
The wavelength of a photon is calculated from its frequency, using the rearranged equation of speed of light equals lambda times frequency.
A practical conversion is shown from meters to nanometers, adding 9 to the exponent of the meter value to get the nanometer value.
The video concludes with a clear demonstration of how to calculate and understand the relationships between wavelength, frequency, and energy in the electromagnetic spectrum.
Transcripts
Browse More Related Video

Electromagnetic Spectrum - Basic Introduction

Visible Light Spectrum Explained - Wavelength Range / Color Chart Diagram - Chemistry
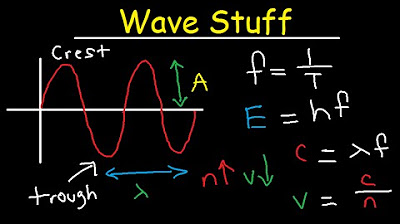
Wavelength, Frequency, Energy, Speed, Amplitude, Period Equations & Formulas - Chemistry & Physics
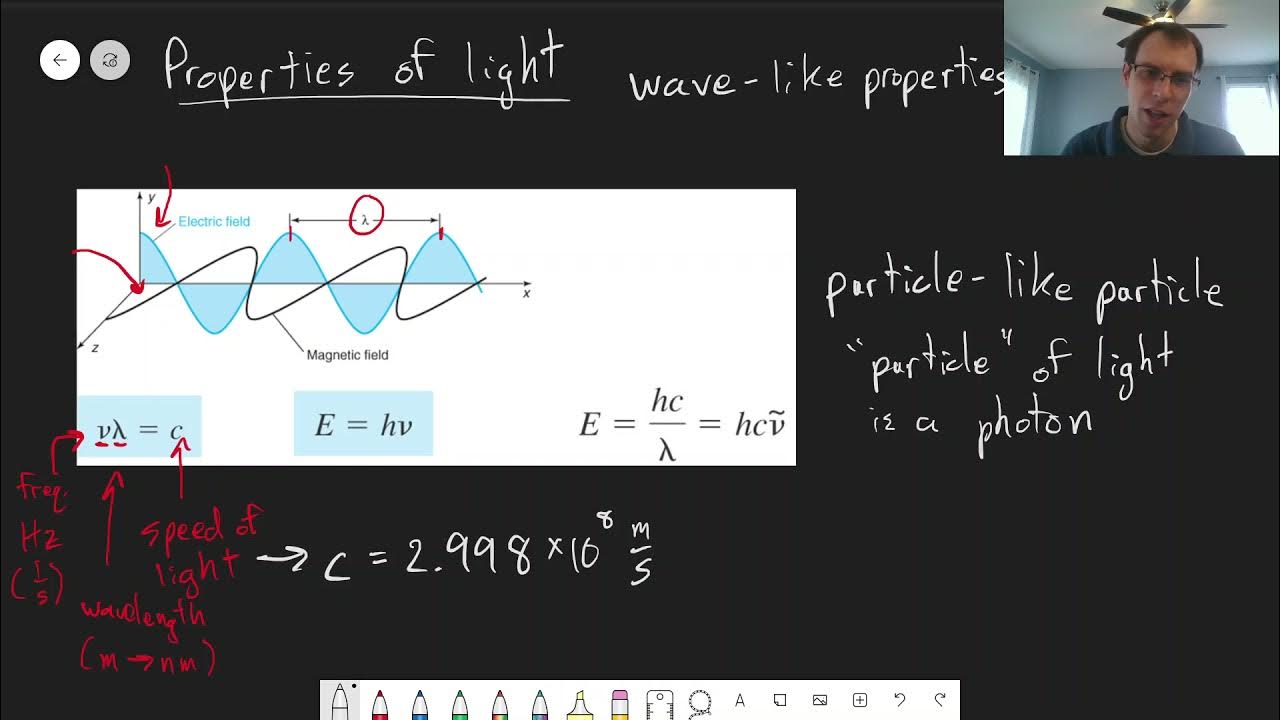
Chapter 18: Properties of Light | CHM 214 | 150
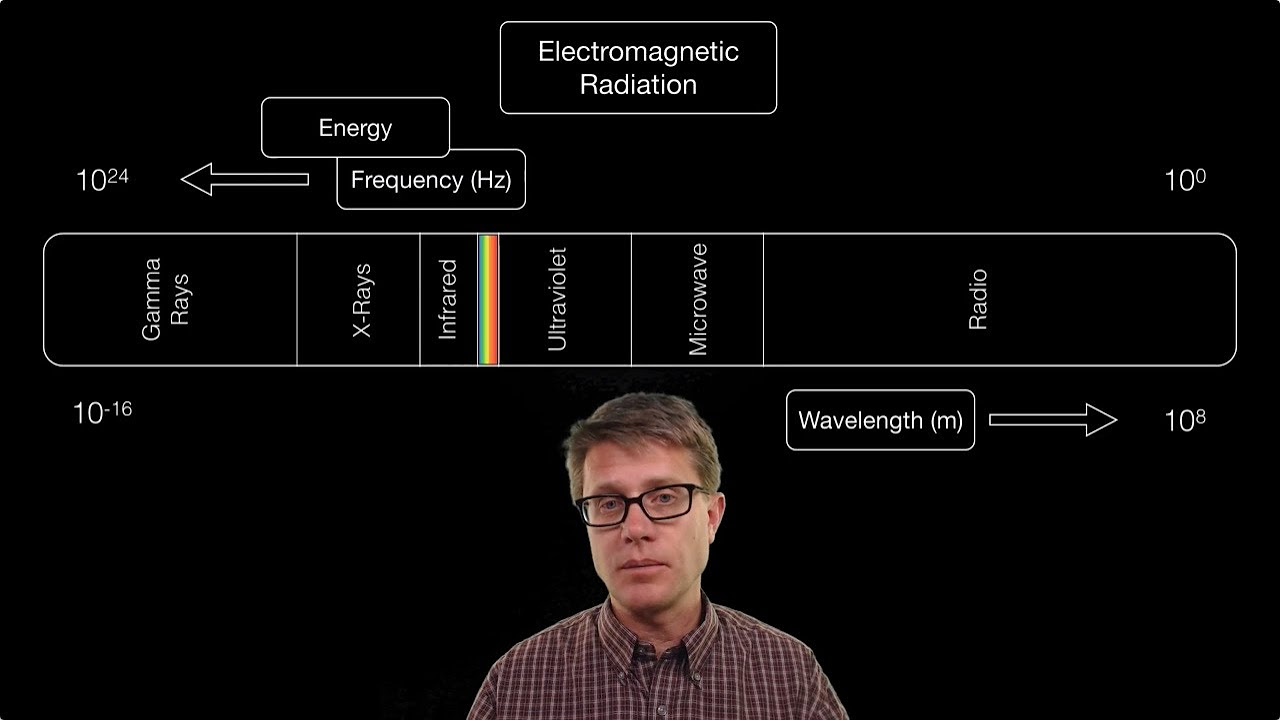
Electromagnetic Radiation
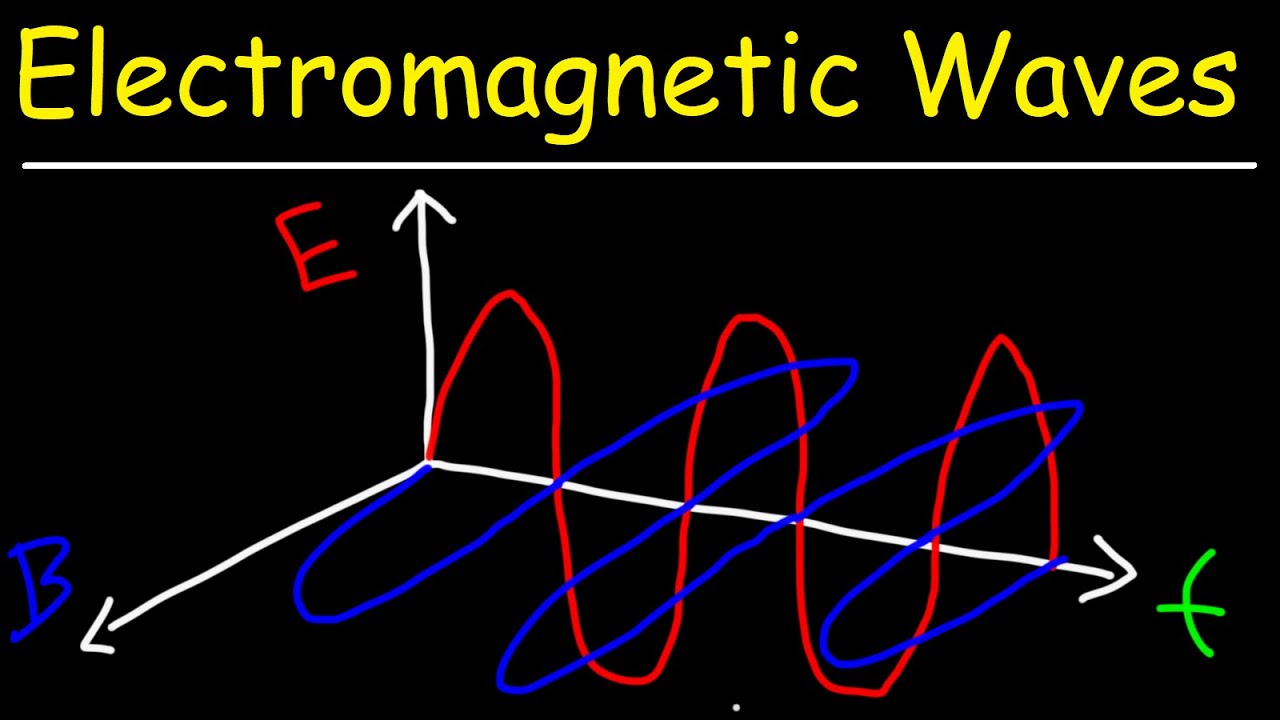
Electromagnetic Waves
5.0 / 5 (0 votes)
Thanks for rating: