Applying the central limit theorem to find probability example 1

Dane McGuckian
12 Jul 201909:09
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a probability problem involving the average age at first marriage for a sample of 32 women in the US, given the average age is 25 with a standard deviation of 4 years. By applying the central limit theorem and converting the ages to z-scores, the video demonstrates how to calculate the probability that the average age at first marriage for this group falls between 26 and 27 years. The final answer provided is 7.70%, showcasing the process of using z-tables and probability calculations for statistical analysis.

Takeaways
  • ๐Ÿ“Š The problem is a probability calculation focused on the average age at first marriage for a sample of 32 women.
  • ๐ŸŽฏ Given data: average age for women is 25, standard deviation is 4 years.
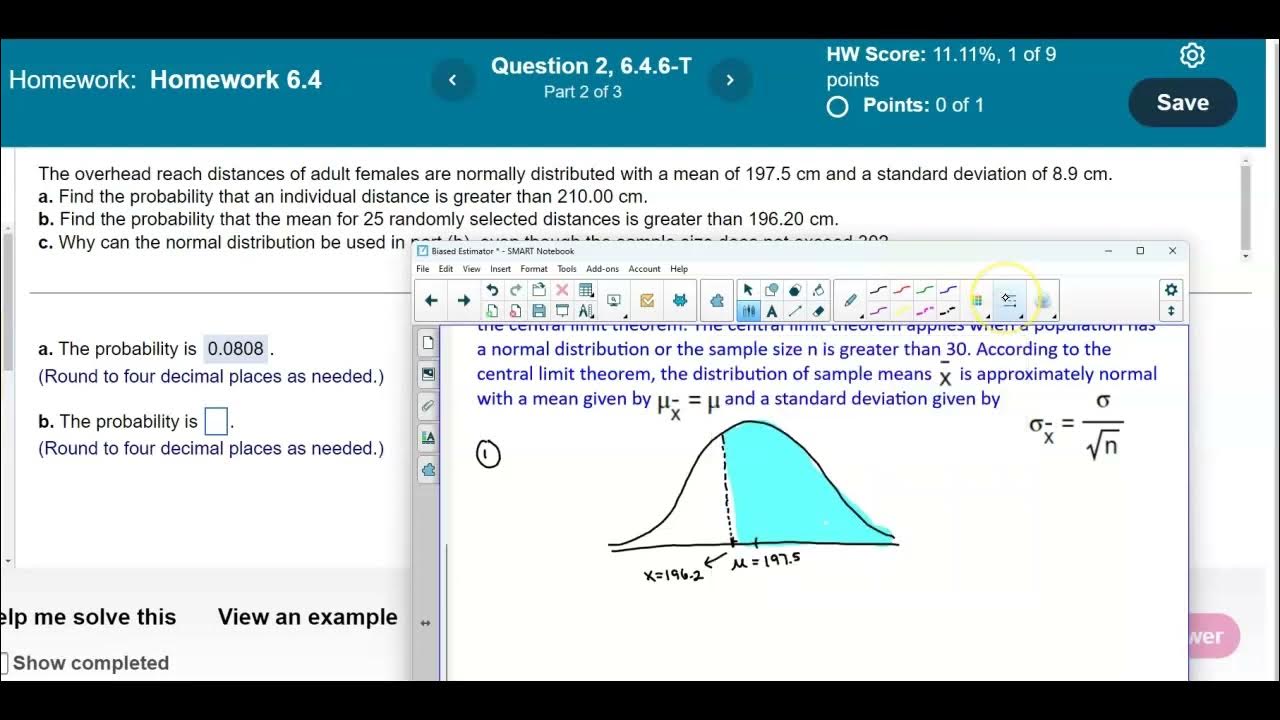
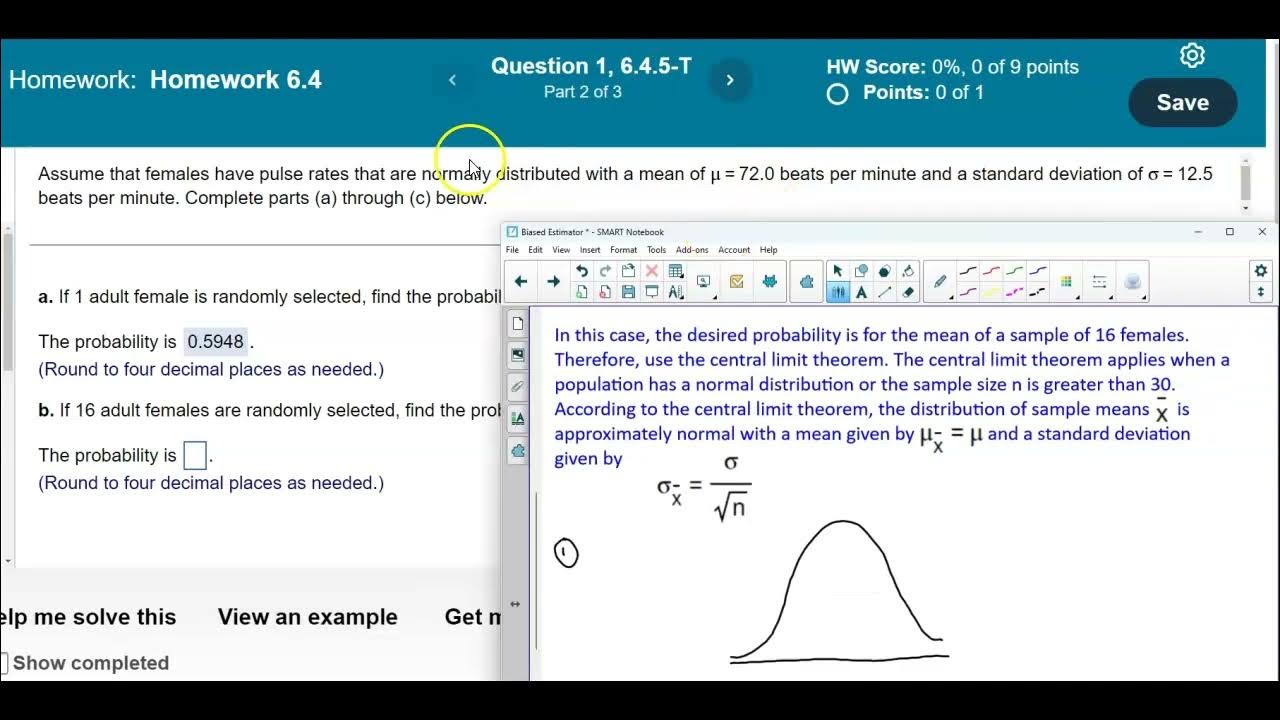
  • ๐Ÿ“ˆ The central limit theorem applies, suggesting that the distribution of sample means is approximately normal when the sample size is large (n > 30).
  • ๐Ÿ”ข The mean for the sample (X bar) remains the same as the population mean, which is 25.
  • ๐Ÿ“ The standard deviation for the sample (X bar) is adjusted by dividing the original standard deviation by the square root of the sample size (n=32).
  • ๐Ÿงฎ The z-scores for the ages 26 and 27 are calculated by the formula: (X - mean) / (standard deviation / โˆšn).
  • ๐Ÿ“ After calculation, the z-score for 26 is approximately 1.41 and for 27 is approximately 2.83.
  • ๐Ÿ” To find the probability, look up the z-scores in a standard normal (Z) table to get the corresponding areas under the curve.
  • ๐Ÿ“Š The area from Z = -1.41 to Z = 2.83 under the curve represents the probability of the average age at first marriage being between 26 and 27.
  • ๐Ÿง  The final probability is obtained by subtracting the smaller area (associated with Z = 1.41) from the larger area (associated with Z = 2.83).
  • ๐Ÿ“ˆ The calculated probability that the average age at first marriage for a random selection of 32 women is between 26 and 27 is 7.70%.
Q & A

  • What is the average age at first marriage for women in the US mentioned in the transcript?

    -The average age at first marriage for women in the US mentioned in the transcript is 25 years.

  • What is the standard deviation for women's age at first marriage according to the transcript?

    -The standard deviation for women's age at first marriage is 4 years.

  • How many women are in the random selection that the problem is referring to?

    -The problem refers to a random selection of 32 women.

  • What is the probability being calculated in the transcript?

    -The probability being calculated is the likelihood that the average age at first marriage for a random selection of 32 women falls between 26 and 27 years.

  • What does X bar represent in this context?

    -In this context, X bar represents the average age at first marriage for the sample of 32 women.

  • Why is the central limit theorem relevant to this problem?

    -The central limit theorem is relevant because it states that the distribution of sample means approaches a normal distribution as the sample size gets larger, which allows us to use the bell curve to solve the problem even if the original data distribution is not known.

  • How does the standard deviation change when calculating for a sample mean?

    -When calculating for a sample mean, the standard deviation is divided by the square root of the sample size (n), which is known as the standard error of the mean.

  • What are the two z-scores calculated in the transcript and what do they represent?

    -The two z-scores calculated are 1.41 and 2.83. They represent the number of standard deviations away from the mean (25) the ages 26 and 27 are, respectively.

  • How is the final probability calculated using the z-scores?

    -The final probability is calculated by looking up the z-scores in the Z table to find the corresponding areas under the normal distribution curve and then subtracting the smaller area from the larger one to find the probability between the two ages.

  • What is the final probability that the average age at first marriage for a random selection of 32 women is between 26 and 27?

    -The final probability that the average age at first marriage for a random selection of 32 women is between 26 and 27 is 7.70% or 0.077 as a decimal.

  • How does the problem illustrate the application of the central limit theorem and z-scores?

    -The problem illustrates the application of the central limit theorem by using the normal distribution to approximate the distribution of sample means, and it uses z-scores to standardize the ages 26 and 27 and find the corresponding probabilities under the normal distribution curve.

  • What is the significance of the square root of the sample size in adjusting the standard deviation?

    -The square root of the sample size is used to adjust the standard deviation because it helps to account for the variability that is reduced in a sample compared to the population as a whole. This adjustment is necessary when calculating the standard error of the mean.

Outlines
00:00
๐Ÿ“Š Probability and Statistics - Understanding Average Age at First Marriage

This paragraph delves into solving a probability problem concerning the average age at first marriage for women in the US. It highlights the importance of recognizing the type of distribution being dealt with and the relevance of the central limit theorem for sample sizes greater than 30. The discussion focuses on identifying the correct mean (ฮผ) and standard deviation (ฯƒ) for the sample of 32 women and how to apply these values to find the probability that the average age at first marriage falls between 26 and 27. The process involves converting the ages to z-scores and using a bell curve to find the required probability.

05:00
๐Ÿ“ˆ Calculating Z-Scores and Probability - Methodology and Application

The second paragraph continues the exploration of the probability problem by detailing the process of calculating z-scores for the ages 26 and 27. It emphasizes the formula for z-scores (X - ฮผ) / ฯƒ and the necessity of adjusting the standard deviation for the sample size by dividing it by the square root of n (in this case, 32). The paragraph walks through the steps of finding the z-scores and using a Z-table to determine the probabilities associated with these scores. Finally, it explains how to combine these probabilities to find the overall probability that the average age at first marriage for a random selection of 32 women falls between 26 and 27, concluding with a final answer of 7.70%.

Mindmap
Keywords
๐Ÿ’กprobability
Probability is a measure of the likelihood that a particular event will occur. In the context of the video, it is used to determine the chance that a random selection of 32 women will have an average age at first marriage between 26 and 27. The video explains how to calculate this probability using statistical methods and the central limit theorem.
๐Ÿ’กaverage age at first marriage
The average age at first marriage is the mean age at which individuals in a population typically get married for the first time. In the video, the average age for women is given as 25, and the problem focuses on finding the probability of a sample of 32 women having an average age at first marriage within a specific range.
๐Ÿ’กstandard deviation
Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. In the video, it is used to describe the variability in the ages at which women get married. The standard deviation for women is given as 4 years, and it plays a crucial role in calculating the probability of the average age at first marriage for a sample of women.
๐Ÿ’กcentral limit theorem
The central limit theorem is a fundamental statistical theory that states that the distribution of sample means approaches a normal distribution as the sample size becomes large, regardless of the population's original distribution. In the video, this theorem allows the use of a bell curve to approximate the distribution of the sample mean (X bar) for the ages at first marriage.
๐Ÿ’กX bar
X bar, often denoted as the sample mean, represents the average of a sample of values from a population. In the video, X bar is used to calculate the average age at first marriage for a group of 32 women, which is the focus of the probability problem.
๐Ÿ’กsample size
Sample size refers to the number of individuals or observations in a sample. In the video, the sample size is 32 women, which is used to determine the distribution of the sample mean and to apply the central limit theorem.
๐Ÿ’กbell curve
A bell curve, also known as a normal distribution curve, is a graphical representation of a normal distribution, which is symmetric and bell-shaped. In the video, the bell curve is used to visualize and calculate the probability of the sample mean falling within a certain range of ages at first marriage.
๐Ÿ’กZ table
A Z table, also known as a standard normal distribution table, provides the cumulative probabilities for a standard normal distribution. In the video, the Z table is used to find the probabilities associated with specific Z scores, which are then used to calculate the probability of the sample mean falling within a certain range.
๐Ÿ’กZ score
A Z score represents the number of standard deviations an individual data point is from the mean in a standard normal distribution. In the video, Z scores are calculated for the ages 26 and 27 and used to look up probabilities in the Z table.
๐Ÿ’กnormal distribution
A normal distribution is a probability distribution in which the probability of a value occurring is highest around the mean and decreases as the value moves away from the mean in either direction. In the video, the normal distribution is approximated for the sample mean of ages at first marriage using the central limit theorem.
๐Ÿ’กstatistical analysis
Statistical analysis is the process of analyzing data through the application of statistical methods, in order to draw conclusions or make predictions. In the video, statistical analysis is performed to calculate the probability of a specific outcome related to the average age at first marriage for a group of women.
Highlights

The problem is a probability calculation involving the average age at first marriage for a sample of 32 women.

The average age at first marriage for women in the US is 25, with a standard deviation of 4 years.

For men, the average age at first marriage is 27.84, but the focus is on women for this problem.

The central limit theorem is key to solving this problem, as it applies to sample sizes greater than 30.

The mean for the sample (X bar) remains the same as the original data set, which is 25 in this case.

The standard deviation for the sample (X bar) must be adjusted by dividing by the square root of the sample size (32).

The probability sought is for the average age at first marriage of 32 women to fall between 26 and 27 years.

Z-scores are used to standardize the data and are calculated by (X - mean) / standard deviation.

The z-score for 26 years is 1.41, calculated as (26-25) / (4/sqrt(32)).

The z-score for 27 years is 2.83, calculated as (27-25) / (4/sqrt(32)).

The Z-table is used to find the probabilities corresponding to the z-scores.

The area to the left of a z-score in the Z-table represents the probability of observing a value less than that z-score.

The probability associated with a z-score of 1.41 is 0.4207.

The probability associated with a z-score of 2.83 is 0.9977.

To find the probability of the average age being between 26 and 27, the probability at the z-score of 2.83 (0.9977) is subtracted from the probability at the z-score of 1.41 (0.4207).

The final probability calculation results in a 7.7% chance (or 0.077 as a decimal) that the average age at first marriage for a random sample of 32 women falls between 26 and 27 years.

This problem demonstrates the application of the central limit theorem, z-scores, and the Z-table in probability calculations for sample means.

Transcripts

Browse More Related Video

Math 14 HW 6.4.6-T Using the Central Limit Theorem

7.2 Sampling Distribution of the Mean (Updated)

Math 14 HW 6.4.5-T Using the Central Limit Theorem

Power

Math 14 HW 6.4.11-T Using the Central Limit Theorem

Sampling distribution example problem | Probability and Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ProbabilityCalculationStatisticalAnalysisMarriageTrendsAgeDistributionCentralLimitTheoremSampleSizeStandardDeviationDataInterpretationZScoresStatisticalInference