How to find Resultant Force - Two Forces Mechanics : ExamSolutions
TLDRThe video script discusses the concept of resultant forces acting on a particle, illustrating how to calculate the equivalent force when multiple forces are applied. It explains the use of trigonometry and vector resolution techniques, such as the cosine rule and Pythagorean theorem, to determine the magnitude and direction of the resultant force when forces are at angles to each other. The examples provided demonstrate the practical application of these methods in solving physics problems involving vector quantities.
Takeaways
- 🌟 When multiple forces act on a particle, they can be replaced by their resultant force, simplifying the analysis of the system.
- 📐 The resultant force (R) from two forces can be calculated using the vector triangle method and trigonometry, such as the cosine rule.
- 📐 The magnitude of the resultant force can also be found by resolving the individual forces into components and using Pythagoras's theorem.
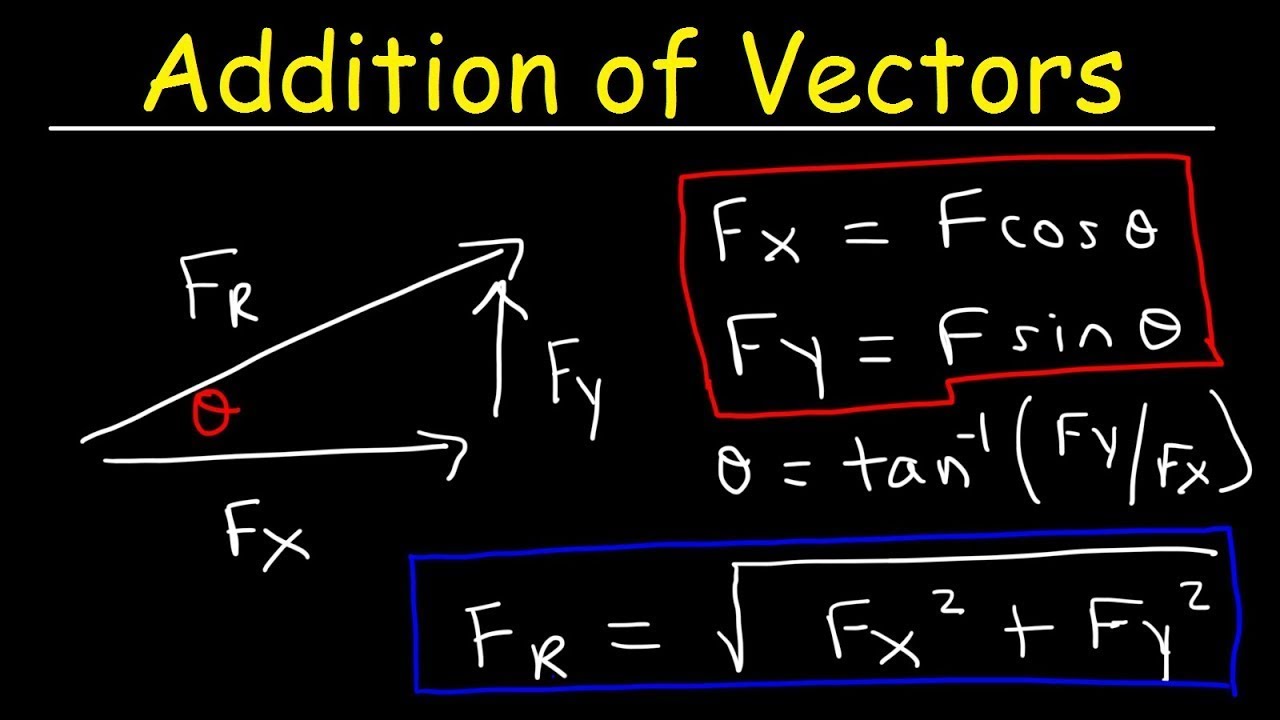
- 🔢 For two forces acting at an angle, the resultant force can be determined by considering the horizontal (X) and vertical (Y) components of the forces.
- 📐 The cosine rule is useful for calculating the magnitude of the resultant force when the forces are known and the angle between them is given.
- 🔄 When resolving forces, the components are calculated based on the angle (using cosine for horizontal and sine for vertical components).
- 🤹 The vector triangle method involves drawing a diagram to scale and using trigonometry to find the resultant force's magnitude and direction.
- 📈 The resultant force's magnitude is the square root of the sum of the squares of the individual forces' components.
- 🔎 It's important to consider the direction of the forces and their components when resolving, as some components may not affect certain axes.
- 🛠️ This method of resolving forces is not only applicable to two forces but can be extended to handle more complex situations with multiple forces acting on a particle.
- 📚 Understanding these concepts is crucial for solving physics problems involving statics and dynamics, where forces and their resultant effects are key to the analysis.
Q & A
What is the resultant force when two forces of 6 Newtons and 4 Newtons act on a particle?
-The resultant force (R) when a 6 Newton force and a 4 Newton force act on a particle is 10 Newtons.
How is the resultant force calculated when two forces act at an angle to each other?
-When two forces act at an angle to each other, the resultant force can be calculated using trigonometry, specifically by forming a vector triangle and applying the cosine rule or by resolving the forces into components and using Pythagoras's theorem.
What is the significance of the vector triangle in force analysis?
-The vector triangle is significant in force analysis as it helps visualize and calculate the resultant force when individual forces are acting at angles to each other. It provides a geometric representation of the vector addition of forces.
What is the cosine rule and how is it applied in calculating the resultant force?
-The cosine rule is a mathematical formula used in trigonometry to determine the length of an unknown side of a triangle when the lengths of the other two sides and the included angle are known. In force analysis, it is applied to calculate the magnitude of the resultant force when individual forces and the angle between them are given.
How can forces be resolved into components?
-Forces can be resolved into components by breaking them down into their individual effects along specific directions, typically perpendicular to each other. This is done using trigonometry, where the components are calculated based on the magnitude of the forces and the angles involved.
What is the Pythagorean theorem and how does it relate to force analysis?
-The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In force analysis, it is used to calculate the magnitude of the resultant force when the components of forces along perpendicular directions are known.
What is the resultant force when an 8 Newton force acts horizontally and a 6 Newton force acts at a 50-degree angle?
-The resultant force in this case can be calculated by resolving the forces into horizontal (X) and vertical (Y) components, and then using Pythagoras's theorem to find the magnitude of the resultant force. The X component is 8 + 6 cos(50 degrees) and the Y component is 6 sin(50 degrees). The resultant force (R) is then the square root of (X^2 + Y^2), which is approximately 12.7 Newtons.
How does the direction of a force affect its components in a resolving technique?
-The direction of a force affects its components in a resolving technique because only the components aligned with the direction of interest contribute to the resultant force. For example, in the case of a force acting at a 50-degree angle, only the sine of the angle (vertical component) is relevant when resolving horizontally, and the cosine (horizontal component) is relevant when resolving vertically.
What is the significance of using significant figures in force calculations?
-Using significant figures in force calculations is important for maintaining accuracy and precision in the results. It ensures that the calculated values are as close as possible to the true values, considering the limitations of measurement and calculation. In the context of the script, rounding to three significant figures is often sufficient for practical purposes.
How can one determine if a force is acting in the direction of the resultant force?
-To determine if a force is acting in the direction of the resultant force, one must consider the angle between the force and the resultant. If the angle is acute and the force is in the same quadrant as the resultant, then the force is contributing to the direction of the resultant. If the angle is obtuse or the force is in a different quadrant, then the force is acting against the direction of the resultant.
What happens when the angle between two forces is 180 degrees?
-When the angle between two forces is 180 degrees, they are acting in opposite directions. The resultant force can be calculated by subtracting the smaller force's magnitude from the larger one, as they effectively act in opposition to each other.
Outlines
🔢 Introduction to Resultant Forces
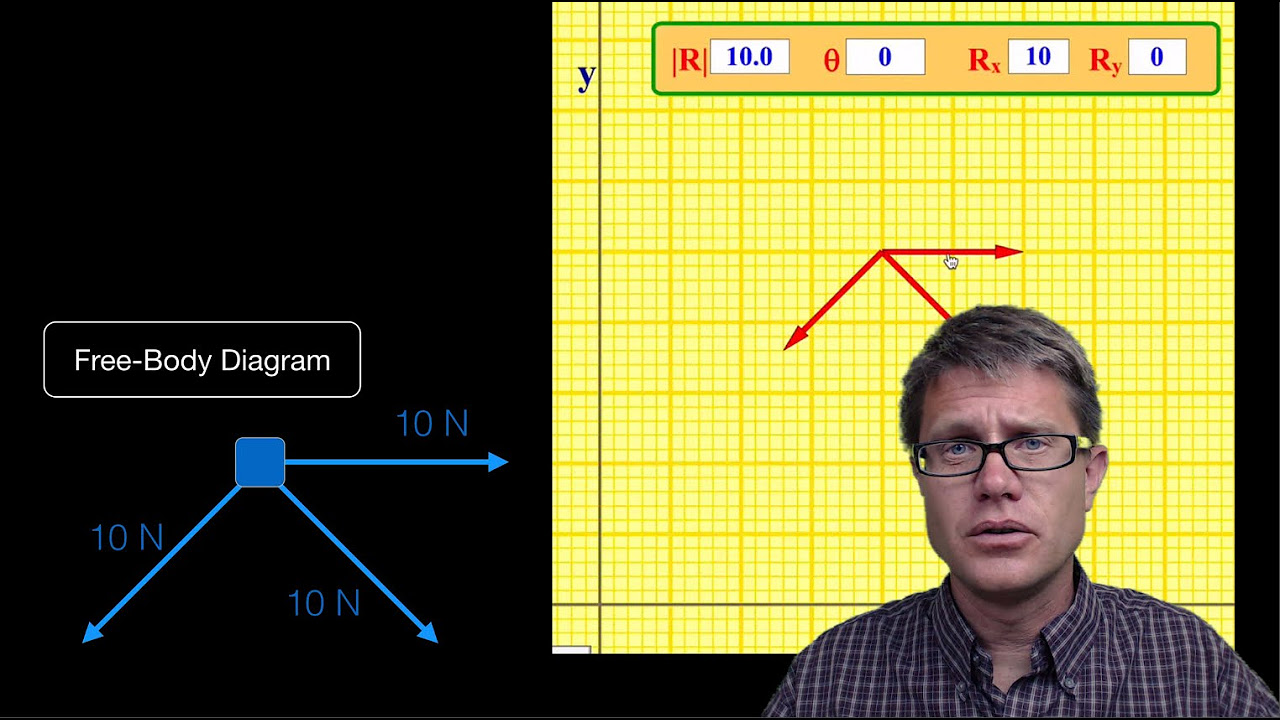
This paragraph introduces the concept of resultant forces acting on a particle. It explains how multiple forces can be combined to find an equivalent single force. The example given is of two forces, one of 6 Newtons and another of 4 Newtons, combining to form a resultant force (R) of 10 Newtons. The paragraph further explains that if another particle is subjected to forces in opposite directions (8 Newtons to the right and 3 Newtons to the left), the resultant force is 5 Newtons to the right. The concept is useful for solving physics problems and is introduced with an analogy to tug-of-war.
📐 Resolving Forces at Angles
This paragraph delves into the resolution of forces acting at angles to each other. It uses the example of a particle subjected to an 8 Newton force and a 6 Newton force at a 50-degree angle. The paragraph explains that forces are vector quantities with both magnitude and direction. It introduces the concept of the force vector triangle and discusses the use of trigonometry, specifically the cosine rule, to calculate the magnitude of the resultant force. The calculation involves finding the square root of the sum of the squares of the individual forces minus twice the product of these forces multiplied by the cosine of the angle between them.
🔄 Component Analysis and Pythagorean Theorem
The paragraph explains an alternative method for resolving forces at angles using components. It describes how to break down the forces into horizontal (X) and vertical (Y) components. The example continues with the 8 Newton and 6 Newton forces at a 50-degree angle, showing how to calculate the X and Y components using trigonometric functions (cosine and sine). The paragraph then applies Pythagoras's theorem to find the magnitude of the resultant force by taking the square root of the sum of the squares of the X and Y components. The method is presented as a practical approach to solving physics problems involving forces at angles.
🎥 Summary and Future Topics
In the concluding paragraph, the speaker summarizes the methods discussed for handling forces acting at angles on a particle. The paragraph reiterates the three approaches: forming a vector triangle and using the cosine rule, scale drawing (though noted as less accurate), and resolving forces into components using trigonometry and Pythagoras's theorem. The speaker also mentions that upcoming videos will provide examples and discuss handling more than two forces, reinforcing the importance of these concepts in physics problem-solving.
Mindmap
Keywords
💡particle
💡forces
💡resultant force
💡vector quantity
💡trigonometry
💡cosine rule
💡resolving technique
💡components
💡Pythagoras's theorem
💡equilibrium
Highlights
The concept of resultant force and its application in physics problems is introduced.
Two forces acting on a particle can be replaced with a single equivalent force known as the resultant force.
The example of combining a 6 Newton force and a 4 Newton force to create a resultant force of 10 Newtons is provided.
A resultant force of 5 Newtons is calculated for a scenario with an 8 Newton force to the right and a 3 Newton force to the left.
The concept of vector quantities and the use of trigonometry to handle forces at angles are discussed.
A detailed explanation of how to resolve forces into components using trigonometry is given.
The cosine rule is mentioned as a method to calculate the resultant force in a non-right-angled triangle.
A step-by-step calculation is provided to find the magnitude of the resultant force using the cosine rule.
An alternative method of resolving forces into components is introduced, which involves breaking down forces into perpendicular directions.
The use of Pythagoras's theorem to calculate the resultant force from its components is explained.
A practical example is given to demonstrate the resolution of an 8 Newton force and a 6 Newton force at a 50-degree angle.
The calculation of the horizontal (X) and vertical (Y) components of the forces is detailed.
The process of finding the resultant force by applying Pythagoras's theorem to the force components is outlined.
The video content aims to provide a better understanding of handling forces at angles in physics problems.
The video mentions future content that will cover more complex scenarios involving multiple forces.
The importance of accurate calculations and methods in solving physics problems is emphasized.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: