Checking Linear Regression Assumptions in R | R Tutorial 5.2 | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
13 Nov 201307:49
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Mike Marin introduces viewers to the process of validating assumptions made during the fitting of a Linear Regression Model. Using the LungCapacity dataset, he demonstrates how to plot data, fit a model, and interpret the summary for model coefficients. Marin explains the importance of checking assumptions like independence, linearity, homoscedasticity, and normality of residuals. He also illustrates how to use R's built-in regression diagnostic plots to assess model fit and assumptions, highlighting the practicality of these tools in scenarios with multiple variables.

Takeaways
  • 📚 The video introduces the process of checking the validity of assumptions made when fitting a Linear Regression Model.
  • 🔍 It emphasizes that while assumptions are never perfectly met, they need to be reasonable enough to work with.
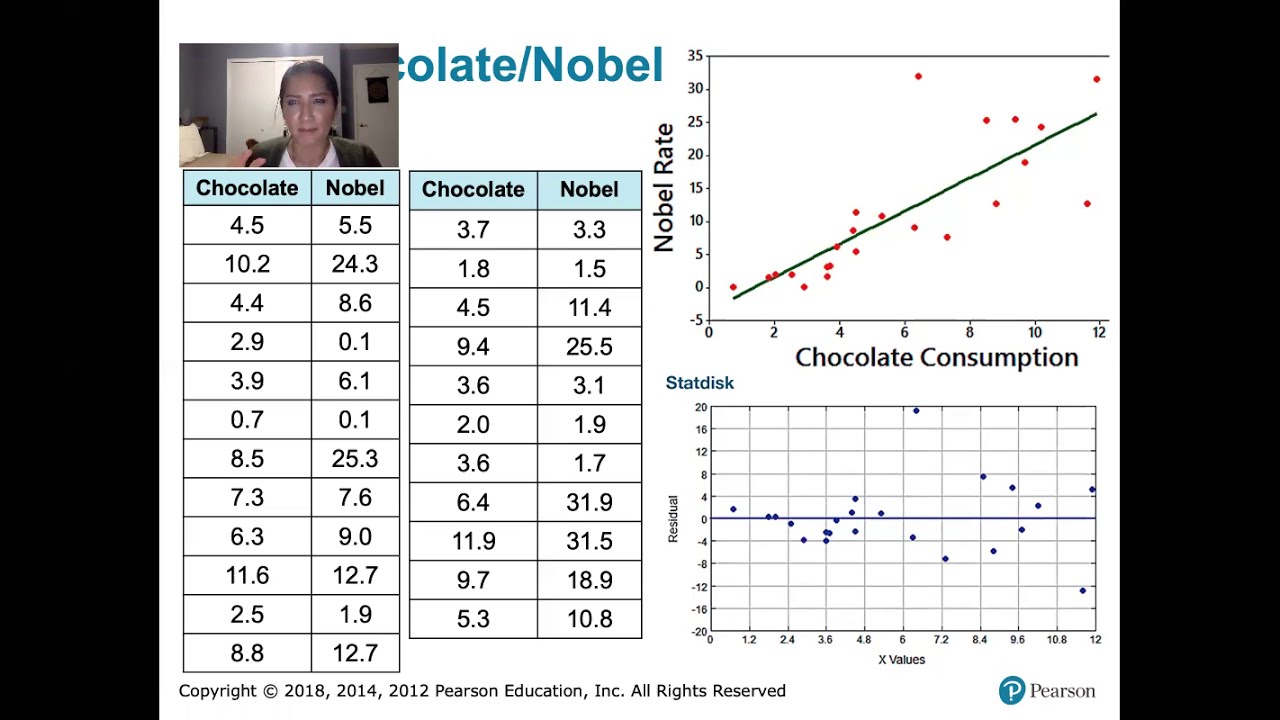
  • 📈 The example used is the LungCapacity dataset, examining the relationship between Age and Lung Capacity.
  • 📊 A Scatterplot is created using the 'plot' command to visualize Age versus Lung Capacity.
  • ⚙️ The 'lm' command is used to fit the Linear Regression Model, and the model is stored in an object named 'MOD'.
  • 📝 The 'summary' command provides estimates of the model's slope and intercept along with other summaries.
  • 📉 The 'abline' command adds a regression line to the Scatterplot, representing the predicted Y values (Y hat).
  • 🔧 The video explains that residuals (errors) are the difference between observed and predicted Y values, and their standard deviation is the Residual Standard Error.
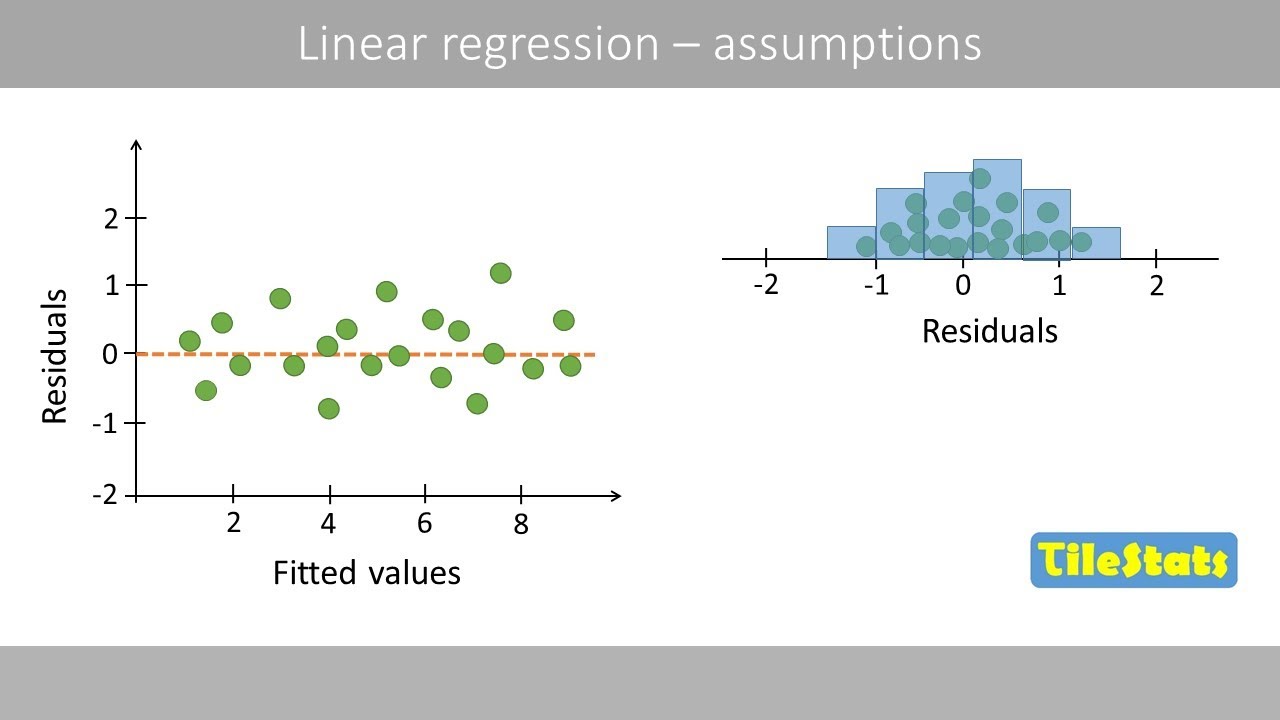
  • 📋 Four key assumptions of Linear Regression are discussed: independence of Y values, linearity, homoscedasticity, and normal distribution of errors.
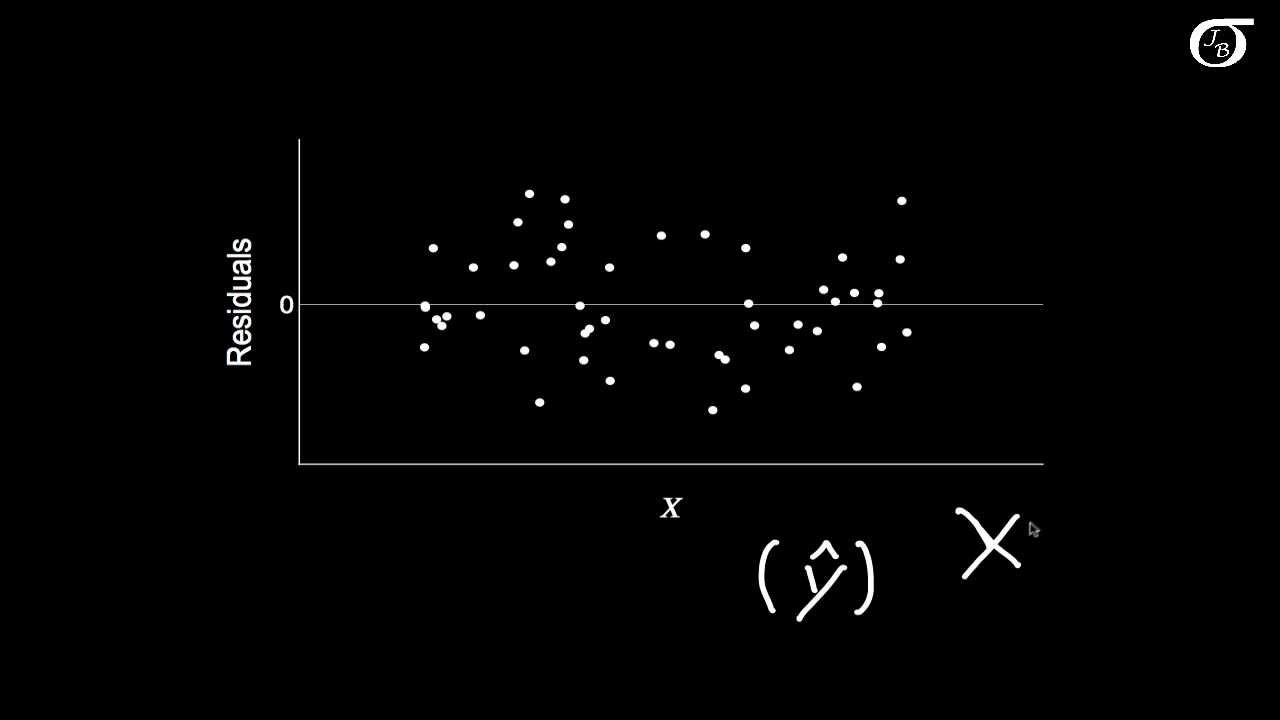
  • 📊 R's built-in regression diagnostic plots help check these assumptions, with the first plot being the Residual plot.
  • 📈 The QQ plot (Quantile-Quantile plot) checks if residuals are normally distributed, with points expected to fall on a diagonal line.
  • 🛠️ The 'mfrow' command is used to display all four diagnostic plots on one screen for easier comparison.
  • 🔬 Non-constant variance is indicated by a megaphone shape in the residual plot, suggesting increasing variance with larger predicted values.
  • 🌐 Non-linearity in the relationship between variables is evident from a curved pattern in the residual plot and other diagnostic plots.
  • 🔑 The importance of diagnostic plots is highlighted for checking assumptions in multiple linear regression models where scatterplots are not feasible.
Q & A

  • What is the main purpose of the video?

    -The main purpose of the video is to introduce how to check the validity of the assumptions made when fitting a Linear Regression Model.

  • Why is it important to check the assumptions of a Linear Regression Model?

    -It is important to check the assumptions because while the assumptions are never perfectly met, we need to ensure they are reasonable enough to work with, which helps in validating the model's reliability and accuracy.

  • What data set is used in the video to demonstrate the process?

    -The LungCapacity data set is used in the video to demonstrate how to check the assumptions of a Linear Regression Model.

  • What is the dependent variable in the model discussed in the video?

    -Lung Capacity is the dependent variable, also known as the outcome variable, in the model discussed in the video.

  • How is a Linear Regression Model typically fitted in R?

    -A Linear Regression Model is typically fitted in R using the 'lm' command, which allows you to specify the dependent and independent variables.

  • What does the 'summary' command in R provide after fitting a model?

    -The 'summary' command in R provides estimates of the model's slope and intercept, along with other summaries that help in understanding the model's performance.

  • What is the meaning of Y hat (Y^) in the context of the video?

    -In the context of the video, Y hat (Y^) represents the predicted or fitted Y value, which is the mean of Y given X.

  • What are residuals in the context of a Linear Regression Model?

    -Residuals are the differences between the observed Y values and the predicted or fitted Y values, and they are labeled with an 'e' in the video.

  • Why are residuals important in checking model assumptions?

    -Residuals are important because they provide insights into the model's fit and help in checking the assumptions such as linearity, homoscedasticity, and normality of the error terms.

  • What is the purpose of the built-in regression diagnostic plots in R?

    -The built-in regression diagnostic plots in R are used to visually assess the validity of the assumptions made when fitting a linear regression model, such as checking for linearity, homoscedasticity, and normality of residuals.

  • What does a 'megaphone shape' in a residual plot indicate?

    -A 'megaphone shape' in a residual plot suggests that the variance is increasing, indicating a violation of the homoscedasticity assumption.

  • What does a curved pattern in the residual plot of a Linear Regression Model imply?

    -A curved pattern in the residual plot implies a non-linear relationship between the variables, indicating a violation of the linearity assumption.

  • Why are diagnostic plots useful when dealing with multiple regression models?

    -Diagnostic plots are useful in multiple regression models because they allow us to check the validity of the assumptions when we have too many variables to visualize the relationship between them, unlike in simple linear regression.

  • What is the significance of the QQ plot in regression diagnostics?

    -The QQ plot, or quantile-quantile plot, is significant as it helps in assessing the normality of the residuals. If the residuals are normally distributed, the points in the QQ plot should fall roughly on a diagonal line.

Outlines
00:00
📊 Introduction to Linear Regression Assumptions

In this segment, Mike Marin introduces the importance of validating assumptions made during the fitting of a Linear Regression Model. He explains that while these assumptions are never perfectly met, it is essential to ensure they are reasonable enough to work with. The video uses the LungCapacity dataset to demonstrate the process of checking these assumptions. The focus is on the relationship between Age and Lung Capacity, with Lung Capacity as the dependent variable. A Scatterplot is used to visualize this relationship, and a Linear Regression Model is fitted using the 'lm' command in R. The summary of the model is then examined to understand the slope, intercept, and other statistical summaries. The concept of residuals and their standard deviation, known as the Residual Standard Error, is introduced as a tool for checking model assumptions.

05:05
🔍 Analyzing Model Residuals for Assumption Validation

This paragraph delves into the examination of model residuals to validate the assumptions of a Linear Regression Model. The assumptions discussed include independence of Y values, linearity, homoscedasticity, and normal distribution of errors. The video demonstrates how to use R's built-in regression diagnostic plots to check these assumptions. Four diagnostic plots are mentioned, which include the Residual plot, QQ plot, and two additional plots that help identify non-linearity and non-constant variance. The 'mfrow' command is introduced to display all four plots simultaneously. The video also addresses the importance of these diagnostic plots, especially in multiple linear regression where visualizing relationships between variables is not possible due to the high dimensionality.

📉 Detecting Non-constant Variance and Non-linearity

In this part of the video, Mike Marin discusses how to identify non-constant variance and non-linearity in a dataset. He presents an example dataset with increasing variance and fits a regression model called model2. The diagnostic plots for this model reveal a megaphone shape in the residual plot, indicating increasing variance with larger predicted values. The linearity assumption is confirmed to be met as the red line in the plot remains flat. The QQ plot shows normal distribution of residuals. Another dataset with a non-linear relationship is then introduced, and a linear model, model3, is fitted to it. The diagnostic plots for this model show a curved pattern in the residual plot, indicating non-linearity. The QQ plot confirms the normal distribution of residuals, but the non-linearity is evident in the other diagnostic plots. The video concludes by emphasizing the utility of diagnostic plots in checking model assumptions, especially in complex models with multiple variables.

Mindmap
Keywords
💡Linear Regression Model
A Linear Regression Model is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data. In the video, the model is used to predict Lung Capacity based on Age, and the script discusses how to validate the assumptions of such a model to ensure its validity.
💡Assumptions
Assumptions in the context of the video refer to the conditions that need to be met for a Linear Regression Model to be valid. These include independence of errors, linearity, homoscedasticity, and normal distribution of residuals. The script emphasizes the importance of checking these assumptions to ensure the model's reliability.
💡Lung Capacity Data
Lung Capacity Data is the dataset used in the video to demonstrate how to check the validity of assumptions in a Linear Regression Model. It is a specific example that helps illustrate the concepts being discussed, such as how to plot data and fit a model to predict Lung Capacity based on Age.
💡Scatterplot
A Scatterplot is a type of plot used to visualize the relationship between two variables. In the video, a Scatterplot of Age versus Lung Capacity is created to examine the linearity assumption, showing how points should be randomly dispersed if the assumption holds.
💡lm Command
The 'lm' command in R is used to fit linear models. In the script, it is used to create a Linear Regression Model predicting Lung Capacity from Age, which is then stored in an object named 'MOD' for further analysis.
💡Summary
In the context of the video, 'Summary' refers to the output provided by the 'summary' command in R, which gives an overview of the fitted model, including estimates of the slope and intercept, and other statistical summaries that help in understanding the model's performance.
💡Residuals
Residuals, labeled with 'e' in the script, are the differences between the observed values of the dependent variable and the values predicted by the model. They are crucial for checking the assumptions of the model, such as homoscedasticity and normal distribution, as discussed in the video.
💡Residual Standard Error
The Residual Standard Error is a measure of the average size of the residuals or errors in a regression model. It is presented in the model's summary and gives an idea of the typical magnitude of the errors, which is important for evaluating the model's fit.
💡Regression Diagnostic Plots
Regression Diagnostic Plots are visual tools used to assess the validity of the assumptions made in a regression model. The script mentions four such plots in R that can help identify issues like non-linearity, non-constant variance, and outliers, which are essential for model validation.
💡Homoscedasticity
Homoscedasticity is the assumption that the variance of the errors is constant across all levels of the independent variable(s). In the video, it is discussed in relation to the appearance of the residual plot, where a constant variation would show as a random scatter of points.
💡Normal Distribution
The assumption of normal distribution of the errors or residuals is important for the validity of a regression model. The QQ plot, one of the diagnostic plots mentioned in the script, is used to check this assumption by comparing the observed residuals to the theoretical quantiles of a normal distribution.
💡mfrow Command
The 'mfrow' command in R is used to specify the arrangement of plots on the screen. In the script, it is used to adjust the layout to display all four diagnostic plots at once, which aids in the comprehensive analysis of the model's assumptions.
💡Non-linear Relationship
A non-linear relationship is a type of relationship between variables that cannot be accurately modeled by a straight line. The script provides an example of this by showing a plot where the relationship between XX and YY is clearly not linear, indicating a violation of the linearity assumption.
💡Multiple Linear Regression
Multiple Linear Regression is an extension of simple linear regression that includes multiple independent variables. The script mentions that the same set of assumptions applies to this model, but visualizing the relationships becomes more complex due to the increased number of variables.
Highlights

Introduction to checking the validity of assumptions in a Linear Regression Model.

Importing and attaching the LungCapacity dataset for analysis.

Explaining the relationship between Age and Lung Capacity as the dependent variable.

Using the 'plot' command to create a Scatterplot of Age vs Lung Capacity.

Fitting a Linear Regression Model with the 'lm' command and storing it as MOD.

Using 'summary' to get model estimates for Slope and Intercept.

Adding a regression line to the plot with the 'abline' command.

Defining Y hat as the predicted or fitted Y value and its formula.

Describing residuals as the difference between observed and predicted Y values.

The importance of the Residual Standard Error in understanding error size.

Assumptions of independence, linearity, homoscedasticity, and normal distribution of errors.

Using R's built-in regression diagnostic plots for assumption checking.

Interpreting the Residual plot for linearity and constant variation.

Understanding the QQ plot for normal distribution of residuals.

Using 'mfrow' to display all four diagnostic plots on one screen.

Identifying non-constant variance in a residual plot with a megaphone shape.

Demonstrating non-linearity in a scatterplot and its effect on diagnostic plots.

The utility of diagnostic plots in multiple linear regression with many variables.

Preview of the next video discussing further examination of model fit.

Transcripts

Browse More Related Video

Multiple Linear Regression in R | R Tutorial 5.3 | MarinStatsLectures

Assumptions in Linear Regression - explained | residual analysis

Regression diagnostics and analysis workflow

Simple Linear Regression in R | R Tutorial 5.1 | MarinStatsLectures

10.2.6 Regression - Residual Plots and Their Interpretation

Simple Linear Regression: Checking Assumptions with Residual Plots

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Linear RegressionModel ValidationR ProgrammingLung CapacityAssumption CheckingData AnalysisScatterplotResidual AnalysisDiagnostic PlotsStatistical ModelingVideo Tutorial