One-sided limits from graphs | Limits | Differential Calculus | Khan Academy
TLDRThe transcript discusses the concept of limits in calculus, particularly one-sided limits. It explains how the limit of a function as it approaches a certain value can differ depending on whether it's approached from the left (negative direction) or the right (positive direction). The existence of a limit at a point requires both one-sided limits to be equal. Examples are provided to illustrate situations where the limit exists and where it does not, highlighting the importance of uniform convergence from both directions.
Takeaways
- 📌 The concept of a function's limit is explored, specifically focusing on how values of the function (f(x)) approach a certain value as the independent variable (x) approaches a specific number.
- 🔍 When approaching a value from the 'negative direction' (x < target value), the superscript '-' is used to denote this direction for the limit.
- 🔼 Conversely, when approaching from the 'positive direction' (x > target value), the superscript '+' is used to indicate this approach.
- 🌟 The limit of a function at a point exists only if both one-sided limits (from the left and the right) are equal to each other.
- 🚫 If the one-sided limits are not equal, the overall limit at that point does not exist, as demonstrated with the function approaching x=2 from both directions.
- 📈 The script provides examples of functions approaching different values (2, 4, 8, and -2) and illustrates how to calculate and interpret one-sided limits.
- 📊 The visual representation of functions and their behavior near certain points is crucial for understanding the concept of limits.
- 🤔 The script encourages viewers to pause and consider the limit behavior for themselves, fostering active engagement with the material.
- 🎯 When the function approaches a value from both the left and the right and the limits are equal, the function is said to have a limit at that point.
- 🌐 The concept of limits is a fundamental aspect of calculus and is essential for understanding the continuity and differentiability of functions.
- 📚 The examples given in the script serve to reinforce the understanding of limits and to demonstrate how to evaluate them for various functions and values.
Q & A
What is the concept of a limit in calculus?
-The concept of a limit in calculus refers to the value that a function or sequence approaches as the input (often denoted as 'x') approaches a particular value. It is a fundamental idea used to understand the behavior of functions, especially at points where they may not be defined or where there is a discontinuity.
How is the notation for the limit of a function as x approaches a value denoted?
-The notation for the limit of a function as x approaches a value is written as `lim (x -> a) f(x)`, where 'a' is the value that x is approaching, and 'f(x)' is the function in question. This notation indicates the value that 'f(x)' tends to as x gets arbitrarily close to 'a'.
What are one-sided limits, and how are they represented?
-One-sided limits refer to the behavior of a function as x approaches a certain value from either the left (negative direction) or the right (positive direction). They are represented by using a superscript on the approach value, such as `lim (x -> a-)` for the left-hand limit and `lim (x -> a+)` for the right-hand limit.
For what reason might a limit not exist?
-A limit might not exist if the function does not approach a unique value as x approaches a certain point from the left and the right. If the left-hand limit and the right-hand limit are not equal, the overall limit at that point does not exist.
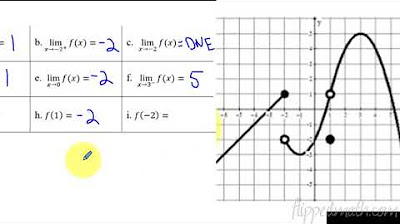
What is the example given in the script where the limit does not exist as x approaches 2?
-The example in the script where the limit does not exist as x approaches 2 is when the function approaches 5 from values less than 2 (left-hand limit) and approaches 1 from values greater than 2 (right-hand limit). Since these two one-sided limits are not the same, the overall limit does not exist.
How can we determine the one-sided limit as x approaches a value from the left?
-To determine the one-sided limit as x approaches a value from the left, we look at the behavior of the function as x takes on values just less than the approach value. We evaluate the function at these nearby points and see if there is a consistent value that 'f(x)' tends towards as x gets closer to the approach value.
What is the significance of the right-hand limit in understanding the behavior of a function?
-The right-hand limit is significant because it shows how the function behaves as x increases and approaches a certain value from the right or positive direction. This is important for understanding the continuity and differentiability of the function, as well as for determining the function's limit as x approaches that value.
In the given examples, which function had a limit of 5 as x approached 4 from both the left and right?
-In the given examples, the function where 'f(x)' approached a limit of 5 as x approached 4 from both the left and right was the one where the one-sided limit from below was equal to negative 5, and the one-sided limit from above was also equal to negative 5, indicating that the function consistently approached 5 from both directions.
What is the example of a function where the limit as x approaches 8 does not exist?
-The example of a function where the limit as x approaches 8 does not exist is when the function approaches 3 from the left (negative direction) and 1 from the right (positive direction). Since these one-sided limits are different, the overall limit as x approaches 8 does not exist.
How can we determine if a limit exists at a certain point for a given function?
-To determine if a limit exists at a certain point for a given function, we must evaluate both the left-hand limit and the right-hand limit as x approaches that point. If both one-sided limits are equal, then the overall limit exists and is equal to the common value of the one-sided limits. If they are not equal, the limit does not exist.
What is the conclusion drawn from the example where the function's one-sided limits as x approaches -2 were both equal to 4?
-The conclusion drawn from the example where the function's one-sided limits as x approaches -2 were both equal to 4 is that the limit exists at this point, and its value is 4. This is because both the left-hand limit and the right-hand limit were found to be equal, satisfying the condition for the existence of a limit.
Outlines
📚 Understanding One-Sided Limits
This paragraph discusses the concept of one-sided limits in the context of a function's behavior as it approaches a specific value. It explains the process of evaluating the limit from both the left (negative direction) and the right (positive direction). The key point is that for a limit to exist at a certain point, both one-sided limits must converge to the same value. The example provided illustrates a scenario where the function approaches different values from the left and right sides of 2, resulting in a non-existent limit. The explanation emphasizes the importance of consistency in one-sided limits for the existence of a limit at a given point.
🔢 Analyzing Limits at a Particular Point
This paragraph continues the exploration of limits by examining the behavior of a function as it approaches the number 4. It highlights the process of evaluating one-sided limits from both the left and the right, and in this case, the function approaches -5 from the left and +5 from the right. The summary points out that when both one-sided limits match, the overall limit at that point exists and is equal to the common value. The paragraph reinforces the idea that the limit of a function at a point is determined by the behavior of the function as it approaches that point from all directions.
Mindmap
Keywords
💡Limit
💡Function
💡Approaching
💡One-sided limits
💡Direction
💡Negative direction
💡Positive direction
💡Discontinuity
💡Exist
💡Undefined
💡Visually
Highlights
Exploring the concept of limits in calculus, specifically one-sided limits.
Approaching the value of x equals 2 from the left, the function f(x) appears to approach 5.
The notation for the limit from the left is denoted by placing a negative superscript after the number 2.
For the limit to exist at x equals 2, both one-sided limits from the left and right must be equal.
In the given example, the function f(x) does not have an existing limit as x approaches 2 because the one-sided limits are not equal.
When approaching x equals 4 from the left, the one-sided limit is negative 5.
The one-sided limit from the right as x approaches 4 also equals negative 5, confirming the limit exists and is equal to negative 5.
The limit of f(x) as x approaches 8 from the left is 3, showing a different behavior from the right approach.
The limit from the right as x approaches 8 is 1, indicating that the two-sided limit does not exist for this case.
The function f(x) is undefined at x equals negative 2, but the one-sided limit from the left appears to be 4.
The one-sided limit from the right as x approaches negative 2 also converges to 4, confirming the limit exists and is equal to 4.
The existence of a limit requires that both left-handed and right-handed limits converge to the same value.
The concept of limits is fundamental in calculus for understanding the behavior of functions at specific points.
The method of approaching a value from the left and right provides insight into the behavior of a function near certain points.
The example demonstrates the importance of one-sided limits in determining the overall limit of a function.
The visual representation of function behavior helps in understanding the concept of limits more intuitively.
The transcript serves as an educational resource for those learning about limits in calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: