2D divergence theorem | Line integrals and Green's theorem | Multivariable Calculus | Khan Academy
TLDRThe video script explores the concept of a line integral around a closed loop in a two-dimensional space, focusing on the dot product of a vector field F with the unit normal vector along a curve. It introduces the idea of using Green's theorem to derive a two-dimensional version of the divergence theorem, illustrating how the rate of particle exit from a contour can be understood in terms of the divergence of the vector field over the enclosed region. The explanation provides a visual and intuitive understanding of the mathematical concepts, emphasizing the relationship between the vector field's divergence and the physical interpretation of particle flow.
Takeaways
- 📐 The concept of a unit normal vector is introduced as a prerequisite for understanding line integrals around a closed loop.
- 🔄 The line integral of a vector field F around a closed loop, in the positive counterclockwise orientation, is being explored.
- 🎨 The integral is represented as the dot product of the vector field F and the unit normal vector at any point on the curve ds.
- 📈 The physical interpretation of the integral involves imagining the vector field as representing the velocity of particles in a two-dimensional gas.
- 🌀 The integral measures the rate at which particles are exiting the contour, with the potential for a net entrance if the result is negative.
- 🌐 The use of Green's theorem is proposed to manipulate the line integral into a more intuitive form.
- 🔄 The manipulation leads to the derivation of a two-dimensional version of the divergence theorem.
- 📐 The normal vector is expressed in terms of the functions P and Q, and its magnitude is related to the differential arc length ds.
- 🔄 By applying Green's theorem, the line integral is related to the double integral over the region enclosed by the contour.
- 📊 The double integral expression is identified as the divergence of the vector field F, multiplied by an infinitesimally small area dA.
- 🌐 The divergence theorem connects the rate of particle flow through the boundary to the divergence of the vector field within the enclosed region.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is the line integral around a closed loop in a vector field F, and its relation to the divergence theorem and Green's theorem.
What is a unit normal vector?
-A unit normal vector is a vector that is perpendicular to the curve at any given point and has a magnitude of one.
How does the dot product of the vector field F and the unit normal vector relate to the physical concept of flow?
-The dot product of the vector field F and the unit normal vector gives the magnitude of the component of the vector field in the normal direction, which can be interpreted as the rate at which particles are exiting or entering the contour in a two-dimensional universe.
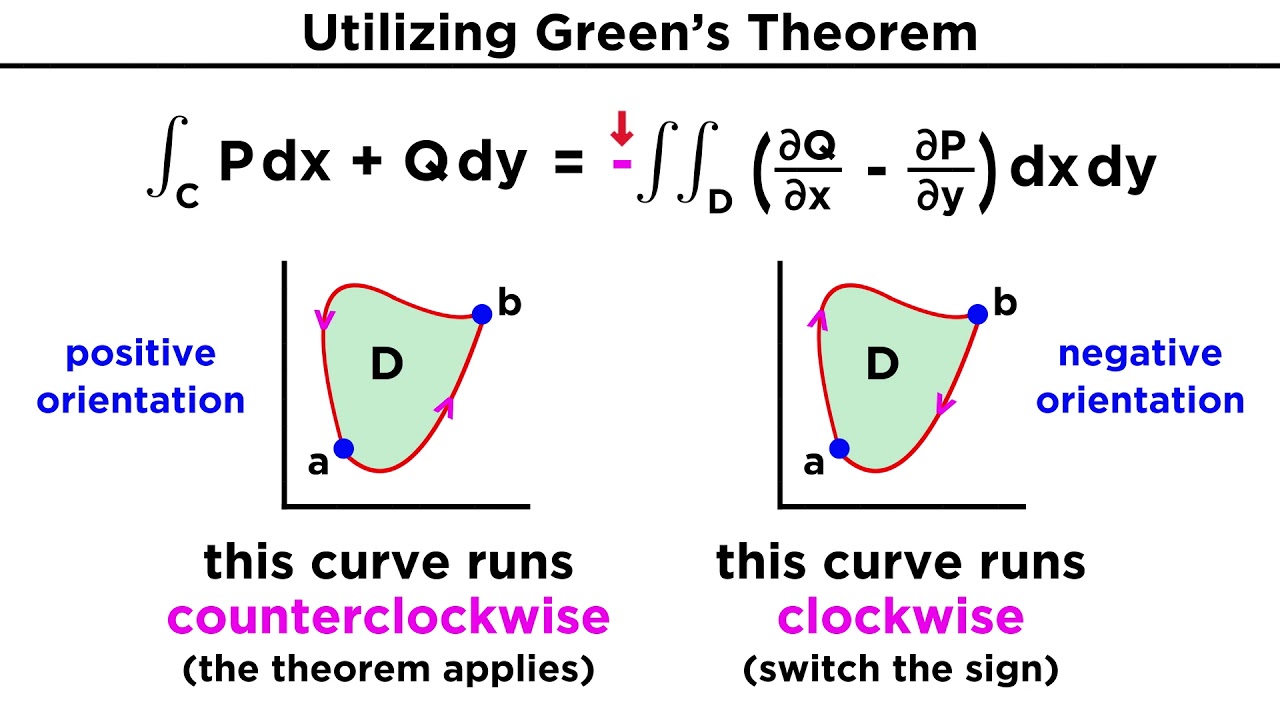
What is the significance of the positive, counterclockwise orientation in the line integral?
-The positive, counterclockwise orientation is significant because it defines the direction in which the line integral is taken around the closed loop, which affects the sign of the result and the interpretation of the flow.
How does Green's theorem relate to the line integral of a vector field around a closed loop?
-Green's theorem relates the line integral of a vector field around a closed loop to a double integral over the region enclosed by the loop, allowing the conversion of a contour integral into an area integral.
What is the two-dimensional version of the divergence theorem?
-The two-dimensional version of the divergence theorem states that the line integral of a vector field F around a closed loop is equal to the double integral of the divergence of F over the region enclosed by the loop.
How does the divergence of a vector field F relate to the flow of particles in the field?
-The divergence of a vector field F measures the rate of expansion or contraction of the field, which can be interpreted as the rate at which particles are moving away from or converging towards a point in the field.
What is the mathematical expression for the magnitude of the unit normal vector?
-The magnitude of the unit normal vector is given by 1/sqrt((dy/dx)^2 + 1), where dy/dx is the derivative of y with respect to x.
What is the role of the coordinate plane in visualizing the vector field and the contour?
-The coordinate plane is used to visualize the vector field and the contour by providing a reference for the x and y coordinates of points in the plane and allowing the depiction of the vector field's vectors at different points.
How does the concept of a two-dimensional universe help in understanding the line integral?
-The concept of a two-dimensional universe helps in understanding the line integral by providing a simplified scenario where particles can only move in the x and y directions, making it easier to visualize and conceptualize the flow of particles and the effects of the vector field.
Outlines
📚 Introduction to Line Integrals and Vector Fields
This paragraph introduces the concept of line integrals around a closed loop, specifically focusing on the positive, counterclockwise orientation. The discussion revolves around the integral of a vector field F dot the unit normal vector along a curve. The instructor aims to explore and manipulate this expression to derive interesting conclusions. The concept is visualized with the help of a coordinate plane and a curve, emphasizing the vector field's association with a point in the plane. The unit normal vector is introduced, and its role in determining the magnitude of the vector field in the normal direction is explained. The paragraph sets the stage for further exploration using Green's theorem and the divergence theorem.
🌀 Understanding the Physical Significance of Line Integrals
In this paragraph, the instructor delves into the physical relevance of the line integral expression by using an analogy of gas particles in a two-dimensional universe. The velocity of these particles at various points is represented by the vector field. The dot product of the vector field and the unit normal vector is interpreted as the speed at which particles are exiting the curve at a given point. By summing these up through the integral, the overall rate at which particles are exiting the contour is determined. The paragraph also transitions into discussing the mathematical manipulation of the line integral, introducing the concept of normal vectors and their construction. The goal is to rewrite the integral in a form that can be analyzed further, eventually leading to the connection with Green's theorem.
📐 Applying Green's Theorem and the Divergence Theorem
The final paragraph focuses on applying Green's theorem to the previously discussed line integral. It demonstrates that the line integral of F dot n around a contour is equivalent to a double integral over the region enclosed by the contour, involving the partial derivatives of the vector field components. This leads to the realization that the expression is essentially the divergence of the vector field F. The divergence, a measure of expansion or contraction of a vector field, is used to interpret the line integral in a more intuitive way. The paragraph concludes by highlighting the significance of this result, showing that the two-dimensional flux through a surface is equivalent to the sum of divergences over the enclosed region. This establishes a connection between the line integral around a contour and the divergence theorem, offering a deeper understanding of the mathematical concepts involved.
Mindmap
Keywords
💡Unit Normal Vector
💡Line Integral
💡Vector Field
💡Divergence Theorem
💡Green's Theorem
💡Dot Product
💡Counterclockwise Orientation
💡Two-Dimensional Version
💡Infinitely Small Length
💡Physical Relevance
💡Divergence
Highlights
Exploring the line integral around a closed loop and its relation to a vector field F.
The vector field F is associated with a vector at any point on the x-y plane, defined by functions of x and y.
The expression F dot n represents the magnitude of the vector field F in the normal direction at a point on the curve.
The line integral of F dot n along the curve gives the rate at which particles are exiting the contour.
The physical relevance of the expression can be visualized in a two-dimensional universe with gas particles.
The line integral can be manipulated using Green's theorem to derive a two-dimensional version of the divergence theorem.
The normal vector can be constructed using dy times i minus dx times j, divided by the length ds.
The expression can be rewritten using the constructed normal vector, leading to the dot product of F and this vector.
The dot product results in a statement similar to Green's theorem, involving the functions P and Q from the vector field F.
Applying Green's theorem reveals that the line integral is equal to the double integral over the region surrounded by the contour.
The double integral expression is the divergence of F times an infinitesimally small area dA.
The divergence of F measures whether things are expanding or contracting, and is integral to understanding the line integral's physical meaning.
The sum of the divergences over the region gives the rate at which particles are exiting the boundary.
The two-dimensional flux is equivalent to the sum of the divergences over the area surrounded by the contour.
The expression F dot n over the contour is essentially the two-dimensional divergence theorem.
The exploration of the line integral and its relation to the vector field F provides a deeper understanding of mathematical concepts in physics.
The use of Green's theorem and the concept of divergence offers a new perspective on the behavior of particles in a two-dimensional universe.
The practical application of these concepts can be used to analyze the motion and behavior of particles in various physical scenarios.
Transcripts
Browse More Related Video

Lec 23: Flux; normal form of Green's theorem | MIT 18.02 Multivariable Calculus, Fall 2007

Divergence theorem proof (part 1) | Divergence theorem | Multivariable Calculus | Khan Academy

Divergence intuition, part 1

3D divergence theorem intuition | Divergence theorem | Multivariable Calculus | Khan Academy

Green's theorem proof (part 2) | Multivariable Calculus | Khan Academy
Green's Theorem
5.0 / 5 (0 votes)
Thanks for rating: