Function (composite and inverse)
TLDRIn this informative video, Si Chamba Jacob introduces the concept of functions, their notation, and how to evaluate them. He explains composite functions and inverse functions with examples, demonstrating how to find the value of x in a function and how to represent one function in terms of another. The video is a comprehensive guide to understanding the basics of functions, their composition, and inversion, suitable for learners seeking to grasp these mathematical concepts.
Takeaways
- 📌 Functions are denoted by symbols like f(x), g(x), or k(x), with x representing the input variable.
- 🔢 To evaluate a function at a specific value, substitute the value for x and perform the calculation.
- 🔍 When finding the value of x, you are given an expression and must solve for x by following algebraic steps.
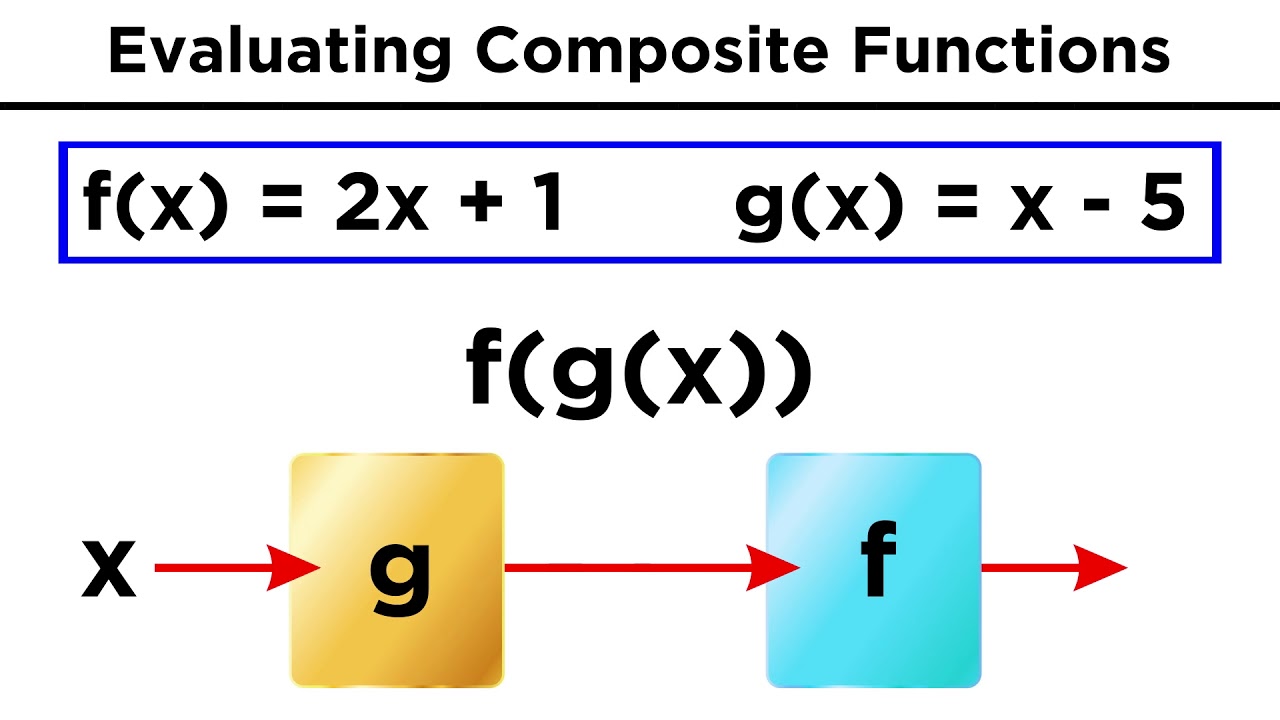
- 🐍 Composite functions are described as one function 'swallowing' another, represented as (f ∘ g)(x) or f(g(x)).
- 🔄 To find the composite function f(g(x)), substitute g(x) into f(x) and simplify the expression.
- 🔄 For the inverse function, switch the roles of x and y in the function and solve for the new y (which becomes x).
- ⏺ To solve for x in a function, you may need to cross-multiply or group like terms to isolate x.
- 📈 The inverse function is found by interchanging x and y in the equation and then solving for y, which becomes the new x.
- 🎯 For example, to find f^(-1)(x), replace f(x) with y, solve for x in terms of y, and then replace y with x to get the inverse function.
- 📚 Understanding functions, their notation, and how to manipulate them is key to solving problems involving functions.
- 👋 The presenter, Si Chamba Jacob, encourages viewers to watch the entire video and engage with his YouTube channel for more content.
Q & A
What is the basic concept of functions discussed in the script?
-The basic concept of functions discussed in the script is that functions are denoted by symbols like f(x), g(x), or k(x), and they represent a relationship where one variable, usually x, is transformed according to some rule. The function is defined by its name and the expression inside the parentheses.
How are functions represented in mathematical notation?
-Functions are represented in mathematical notation by a letter, such as f, g, or k, followed by the variable x in parentheses. The letter under the parentheses indicates the function's name, and the x inside the parentheses represents the input variable.
What is the significance of the letter 'x' in a function?
-The letter 'x' in a function represents the input variable. It is the value that is being transformed or acted upon by the function according to its rule or expression.
How does one evaluate a function at a specific value?
-To evaluate a function at a specific value, you replace the variable (usually x) in the function's expression with the given value and then perform the necessary arithmetic operations to find the output.
What is the process of finding the value of x when given a function and an output value?
-To find the value of x when given a function and an output value, you set the function equal to the output value and solve for x by isolating it on one side of the equation. This often involves algebraic manipulation such as cross-multiplication or grouping like terms.
What is a composite function and how is it represented?
-A composite function is a function that is formed by applying one function to the result of another function. It is represented by writing the function that is being 'swallowed' (the inner function) inside the function that does the 'swallowing' (the outer function), like (f ∘ g)(x) or f(g(x)).
How does the script illustrate the concept of composite functions?
-The script illustrates the concept of composite functions by using an analogy of a snake swallowing another snake. It explains that when one function 'swallows' another, the inner function is evaluated first, and then the outer function operates on the result of the inner function.
What is the inverse of a function and how is it found?
-The inverse of a function is a function that reverses the effect of the original function. It is found by switching the roles of x and y in the original function's equation and then solving for y, which gives you the inverse function.
How does the script describe the process of finding the inverse of a function?
-The script describes the process of finding the inverse of a function by first replacing the function's output (usually denoted by y) with the inverse function's input (x), and then solving the equation for the new output variable (which becomes the inverse function).
What is the significance of the video's author's name in the context of the script?
-The significance of the video's author's name, Si Chamba Jacob, is that it provides the context for the instructional content. It identifies the person delivering the information and adds credibility to the explanations provided in the script.
How does the script use examples to clarify the concepts of functions?
-The script uses examples to clarify the concepts of functions by walking through the steps of evaluating functions, finding the value of x for given outputs, and calculating composite and inverse functions. These examples provide a practical application of the theoretical concepts discussed.
What is the final call to action given by the video's author?
-The final call to action given by the video's author is for viewers to subscribe to his YouTube channel and follow his works, indicating that there is more content available for those interested in learning more about functions and related mathematical concepts.
Outlines
📚 Introduction to Functions and Notations
This paragraph introduces the concept of functions, their basic notations, and how to read and interpret them. The speaker, Si Chamba Jacob, explains that functions are denoted by symbols like f(x), g(x), or k(x), with x representing the input. He provides examples of how to evaluate functions, such as f(x) = 3x - 1 and g(x) = 1 - x^2, and demonstrates how to find the value of a function at a specific point, like f(2) or g(0). The paragraph emphasizes the importance of understanding the structure of functions and how to work with them in various mathematical contexts.
🔍 Solving for x and Understanding Composite Functions
In this section, the speaker discusses how to find the value of x when given an equation involving functions. He uses an example to illustrate the process of solving for x by equating the functions and isolating x. The concept of composite functions is introduced, using a snake analogy to explain how one function can 'swallow' or be contained within another. The speaker then provides a detailed example of finding the composite function f(g(x)) by substituting the entire function g(x) into f(x), highlighting the step-by-step process of simplification.
🔄 Finding Inverse Functions
This paragraph focuses on the concept of inverse functions, explaining that they represent the opposite transformation of a given function. The speaker provides a clear methodology for finding the inverse of a function by swapping the roles of x and y (or f(x)) and solving for the new y (or f^(-1)(x)). Two examples are given, one for each function f(x) = 2x + 5 and g(x) = (x - 3) / 2, to demonstrate how to rearrange the equation and solve for the inverse function. The process involves making y the subject, isolating x, and then solving for the inverse function in a step-by-step manner.
🙌 Conclusion and Call to Action
The speaker concludes the video by summarizing the key points covered in the script, including the evaluation of functions, solving for x, understanding composite functions, and finding inverse functions. He encourages viewers to subscribe to his YouTube channel and follow his works, indicating that the content has been designed to be informative and engaging. The call to action serves as a reminder for viewers to engage with the speaker's content and continue learning about mathematical concepts.
Mindmap
Keywords
💡Functions
💡Composite Functions
💡Inverse Functions
💡Evaluation
💡Variable
💡Substitution
💡Equation
💡Solving
💡Algebraic Manipulation
💡YouTube Channel
💡Educational Content
Highlights
Introduction to functions and their notation, such as f(x), g(x), or k(x).
Explanation of how to read and work with functions, including finding f(2) and g(0).
Process of solving for a value in a function, like finding the value of x when f(x) = 6.
Illustration of composite functions and the concept of one function 'swallowing' another.
Detailed example of finding the composite function f(g(x)) with given functions f(x) and g(x).
Introduction to inverse functions and their concept as the 'opposite' of the original function.
Method for finding the inverse of a function, including the steps and algebraic manipulations.
Example of finding the inverse of f(x) = 2x + 5 and presenting the solution f^(-1)(x) = (x - 5) / 2.
Example of finding the inverse of g(x) = (x - 3) / 2 and presenting the solution g^(-1)(x) = 2x + 3.
The importance of understanding function notation and how it relates to the operations performed on the functions.
The practical application of functions in solving mathematical problems and their real-world relevance.
The use of algebraic techniques to manipulate and solve for values within the context of functions.
The concept of substitution in functions and how it is used to evaluate and compute function values.
The role of functions in mathematical modeling and their application in various fields.
The clear and structured approach to teaching functions, making complex concepts accessible to learners.
The comprehensive coverage of functions, including composition and inversion, providing a solid foundation for further study.
Transcripts
Browse More Related Video

Calculus made EASY! 5 Concepts you MUST KNOW before taking calculus!

Algebra/Composition of Functions!

10 - What are Composite Functions? (Part 1) - Evaluating Composition of Functions & Examples
Manipulating Functions Algebraically and Evaluating Composite Functions

Composition of Functions (Precalculus - College Algebra 48)

Composite Function Explained - The Basics You NEED To Know!
5.0 / 5 (0 votes)
Thanks for rating: