Basic Integration Problems
TLDRThis video script offers a comprehensive guide to basic integration rules, covering the integration of constants, differentials, and the application of the power rule for both polynomial and rational functions. It also delves into the anti-derivatives of trigonometric functions, exponential functions, and logarithmic functions, providing examples and emphasizing the importance of recognizing when the variable is a linear function or when the derivative is a constant for successful integration.
Takeaways
- 📚 Basic integration involves finding the antiderivative of a given function, typically denoted by adding 'plus C' for a constant of integration.
- 🔢 Integrating a constant with a variable results in the constant times the variable plus C (e.g., ∫k dx = kx + C).
- ✍️ The power rule states that the antiderivative of x^n dx is (x^(n+1))/(n+1) + C.
- 🌟 Examples of power rule application: ∫x^2 dx = (x^3)/3 + C, ∫x^4 dx = (x^5)/5 + C, and ∫1/x^2 dx = -1/x + C.
- 📐 When dealing with rational functions, they may need to be rewritten in a suitable form before applying the power rule.
- 🌈 The antiderivatives of basic trigonometric functions are memorized formulas: ∫cos(x) dx = sin(x) + C, ∫sin(x) dx = -cos(x) + C, and so on.
- 🔍 For trigonometric integrals, like ∫8cos(x) + 3sin(x) dx, the process involves finding the antiderivative of each term separately and combining the results.
- 📶 The integration of exponential functions follows the form ∫e^u du = e^u/u' + C, where u' is the derivative of u and must be a constant.
- 🧮 Logarithmic functions are integrated using the rule ∫1/u du = ln|u|/u' + C, with u' being a constant.
- 🔄 Confirming integration results can be done by differentiating the result to see if it matches the original function.
- 📊 The script provides a comprehensive overview of basic integration techniques, including constants, power rule, rational functions, trigonometric, exponential, and logarithmic functions.
Q & A
What is the basic integration rule for integrating dx?
-The basic integration rule for integrating dx is x plus a constant c.
How do you integrate a constant with respect to x?
-When integrating a constant with respect to x, the result is kx plus a constant c, where k is the constant being integrated.
What is the power rule for integration and how is it applied?
-The power rule for integration states that the anti-derivative of x raised to the n, dx, is equal to x raised to the n plus one divided by n plus one, plus a constant c.
How do you find the anti-derivative of x squared dx using the power rule?
-Using the power rule, the anti-derivative of x squared dx is x cubed over 3 plus c.
What is the antiderivative of the function 1/x squared?
-The antiderivative of 1/x squared is negative one over x plus a constant c.
What are the antiderivatives of the six basic trigonometric functions mentioned in the script?
-The antiderivatives are: cos(x) becomes sin(x), sin(x) becomes -cos(x), sec(x) becomes tan(x), tan(x) becomes sec(x) plus c, csc(x) squared becomes -cot(x) plus c, and cot(x) becomes -csc(x) plus c.
How do you integrate a rational function like 7/(x to the fourth power)?
-First, rewrite the function as 7x to the negative four, then apply the power rule to get -7/3 * x to the third power plus c.
What is the antiderivative of the exponential function e to the 4x?
-The antiderivative of e to the 4x is e to the 4x divided by the derivative of 4x, which is 4, plus a constant c.
How do you confirm the correctness of an antiderivative found using integration by parts?
-To confirm the correctness, differentiate the found antiderivative and check if it equals the original function.
What is the antiderivative of the logarithmic function 1/u du?
-The antiderivative of 1/u du is the natural log of u divided by u prime, assuming u is a linear function and u prime is a constant.
How do you integrate a function that involves both trigonometric and exponential parts, like 8 cos(x) + 3 sin(x) dx?
-Integrate each part separately using their respective antiderivatives: 8 times sin(x) for cos(x) and -3 times cos(x) for sin(x), and then combine them with a plus c at the end.
Outlines
📚 Basic Integration Rules and Examples
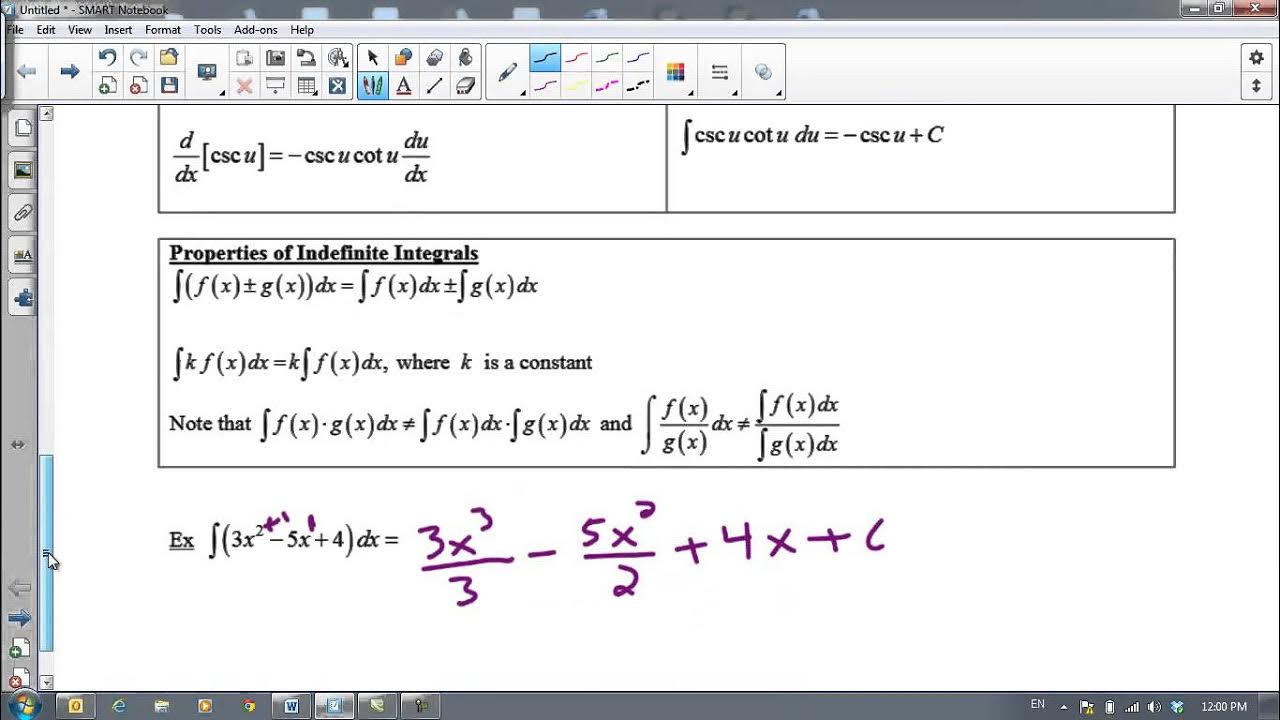
This paragraph introduces fundamental integration rules, starting with the integration of basic variables like dx, dy, and dt, which result in x+c, y+c, and t+c respectively. It then explains how to integrate constants with variables, such as kx+c for a constant k times dx. The power rule is introduced, stating that the anti-derivative of x^n dx is x^(n+1)/(n+1) + c. Several examples are provided to illustrate the application of the power rule, including the anti-derivatives of x^2, x^3, 10x^4, and 1/x^2. The paragraph emphasizes the importance of rewriting expressions before applying the power rule and concludes with examples involving rational functions.
📈 Anti-Derivatives of Trigonometric and Exponential Functions
This paragraph delves into the anti-derivatives of six trigonometric functions, highlighting that the antiderivative of cosine x is sine x, and vice versa, while secant squared is tangent x. It also covers the anti-derivatives of secant x and cosecant squared, emphasizing the need to memorize these relationships. The paragraph then provides example problems integrating trigonometric functions, such as 8cos(x) + 3sin(x)dx and 4sec^2(x) - sec(x)tan(x)dx. It also discusses integrating exponential functions, explaining the method when the exponent is a linear function or a constant, and provides examples, including e^(4x) and e^(7x-3)dx. The paragraph concludes by addressing a case where the method does not apply due to the absence of a constant derivative.
📊 Integration of Logarithmic Functions and Confirmation Through Differentiation
The final paragraph focuses on the integration of logarithmic functions, where the antiderivative of 1/u du is the natural log of u divided by the derivative of u. It clarifies that this method applies when u is a linear function and its derivative is constant. The paragraph provides examples of integrating 1/x and 1/(4x-3), and confirms the results by differentiating them back to the original expressions. It also covers the integration of a function involving 7/(3x-8), demonstrating the process of moving constants and applying the logarithmic integration rule, and confirms the result through differentiation.
Mindmap
Keywords
💡Integration
💡Constant of Integration
💡Power Rule
💡Rational Functions
💡Trigonometric Functions
💡Exponential Functions
💡Logarithmic Functions
💡Antiderivatives
💡Integration by Rewriting
💡Derivative
Highlights
Basic integration rules are discussed, including integrating dx, which results in x plus a constant.
When integrating a constant with a variable, such as kx, the result is kx plus a constant.
The power rule for integration is introduced, which states that the integral of x^n dx is x^(n+1)/(n+1) plus a constant.
Examples of using the power rule include integrating x^2 to get x^3/3 + c and x^3 to get x^4/4 + c.
Integration of rational functions is discussed, with an example of integrating 7/x^4, which results in -7/3 * x^3 + c.
Anti-derivatives of trigonometric functions are provided, such as the integral of cosine x being sine x + c.
Integration of products of trigonometric functions, like cosecant x times cotangent x, is demonstrated.
Integration of exponential functions is covered, with the formula e^u = e^u/u' + c, where u' is the derivative of u.
The integration of logarithmic functions is explained, using the formula ln(u) = (1/u') * ln(u) + c.
The process of confirming integration results through differentiation is illustrated, ensuring the original function is obtained.
Integration of a sum of trigonometric functions, such as 8cos(x) + 3sin(x) dx, is shown to result in 8sin(x) - 3cos(x) + c.
Integration of a combination of secant and tangent functions is demonstrated, resulting in 4tan(x) - sec(x) + c.
The concept of rewriting functions before integrating is emphasized, as seen when integrating 1/x^2 which becomes x^(-2).
Integration of radical functions, like the cube root of x, is discussed using the power rule to obtain (3/4)x^(4/3) + c.
The anti-derivative of secant squared is tangent x, and the anti-derivative of secant x is tangent x + c.
The anti-derivative of cosecant squared is negative cotangent x + c, and the anti-derivative of cosecant x is negative cosecant x + c.
Integration of a function involving both cosecant and cotangent is shown, resulting in cotangent x - cosecant x + c.
The process of integrating a function with a linear term and a constant, like 7/(3x - 8), is demonstrated to result in 7/3 * ln(3x - 8) + c.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: