Gas Laws - Equations and Formulas
TLDRThis transcript delves into the fundamental concepts and equations governing gas behavior, such as pressure, volume, and temperature relationships in the ideal gas law (PV=nRT). It explains Boyle's, Charles's, and Gay-Lussac's laws, highlighting how changes in temperature and pressure affect gas volume. The concept of molar volume and Avogadro's law are discussed, along with gas density calculations and the impact of molar mass and temperature on gas properties. Dalton's law of partial pressures and Graham's law of effusion are also covered, illustrating the interplay between gas molecules, their mass, and their movement in various conditions.
Takeaways
- 📐 Pressure is defined as force per unit area (P = F/A), with units of Pascals (Pa), where 1 Pa = 1 N/m².
- 📐 The ideal gas law is given by PV = nRT, where P is pressure, V is volume, n is moles, R is the gas constant, and T is temperature in Kelvin.
- 📐 The relationship between pressure and volume at constant temperature is described by Boyle's Law (P1V1 = P2V2), showing an inverse relationship.
- 📐 Charles Law relates volume and temperature at constant pressure (V1/T1 = V2/T2), indicating a direct proportionality between volume and temperature.
- 📐 Gay-Lussac's Law connects pressure and temperature at constant volume (P1/T1 = P2/T2), showing that pressure increases with temperature.
- 📐 Avogadro's Law states that at constant temperature and pressure, the volume of a gas is directly proportional to the number of moles (V1/n1 = V2/n2).
- 📐 The molar volume of an ideal gas at STP (Standard Temperature and Pressure) is 22.4 liters per mole.
- 📐 Gas density is calculated as mass per unit volume (Density = m/V) and is influenced by the gas's molar mass, pressure, and temperature.
- 📐 Dalton's Law of Partial Pressures states that the total pressure of a gas mixture is the sum of the partial pressures of its individual components.
- 📐 Graham's Law of Effusion relates the rate of gas effusion to the square root of the reciprocal of the molar mass, with lighter gases effusing faster than heavier ones.
- 📐 The root mean square velocity of a gas (v_rms) can be calculated using the equation v_rms = √(3RT/M), where R is the gas constant, T is the temperature in Kelvin, and M is the molar mass in kilograms per mole.
Q & A
What is the definition of pressure in the context of physics?
-Pressure is defined as the force applied per unit area. It is measured in units of newtons per square meter, which is equivalent to pascals.
How is the pressure related to the units of atmosphere (atm), torr, and millimeters of mercury (mmHg)?
-One standard atmosphere (atm) is equivalent to 760 torr or 760 millimeters of mercury (mmHg). Additionally, 1 atm is equal to 101.3 kilopascals, which is the same as 101,300 pascals.
What is the ideal gas law equation and what does it represent?
-The ideal gas law equation is PV = nRT, where P represents pressure, V is volume, n is the number of moles, R is the gas constant, and T is the temperature in Kelvin. This equation describes the behavior of an ideal gas under various conditions of temperature, volume, and pressure.
What are the units for the gas constant (R) in the ideal gas law equation?
-The gas constant (R) can have different units depending on the version used. One common version is 0.08206 liters times atmospheres per mole per Kelvin (L·atm/mol·K). Another version is 8.3145 joules per mole per Kelvin (J/mol·K).
How does the temperature conversion from Celsius to Kelvin work?
-To convert a temperature from Celsius to Kelvin, you add 273.15 to the Celsius temperature. A simpler approximation is to add 273.
What is Boyle's Law and how does it describe the relationship between pressure and volume?
-Boyle's Law states that at a constant temperature and amount of gas, the pressure of a gas is inversely proportional to its volume. This means that as the volume of a gas increases, the pressure decreases, and vice versa.
What is Charles's Law and how does it relate volume and temperature in a gas?
-Charles's Law states that, at a constant pressure and amount of gas, the volume of a gas is directly proportional to its temperature in Kelvin. Doubling the temperature will double the volume, tripling the temperature will triple the volume, and so on.
What is Gay-Lussac's Law and how does it connect pressure and temperature?
-Gay-Lussac's Law states that, at a constant volume and amount of gas, the pressure of a gas is directly proportional to its temperature in Kelvin. Increasing the temperature will result in an increase in pressure, and vice versa.
What is Avogadro's Law and how does it describe the relationship between moles and volume?
-Avogadro's Law states that at a constant temperature and pressure, the volume of a gas is directly proportional to the number of moles of the gas. This means that doubling the moles of gas in a container will double the volume, assuming the container can expand.
What is the significance of the molar volume of a gas at standard temperature and pressure (STP)?
-At STP, one mole of any ideal gas occupies a volume of 22.4 liters. This value is known as the molar volume and is a constant used in various gas law calculations.
How is the density of a gas calculated and what units are typically used?
-The density of a gas is calculated as the mass of the gas divided by its volume. The typical units for gas density are grams per liter (g/L), with the mass usually given in grams and the volume in liters.
What is Dalton's Law of Partial Pressures and how does it relate to total pressure and individual gas pressures?
-Dalton's Law of Partial Pressures states that the total pressure of a mixture of non-reacting gases is equal to the sum of the partial pressures of the individual gases. The partial pressure of a gas is the pressure that the gas would exert if it were alone in the container, and it is calculated as the product of the gas's mole fraction and the total pressure.
Outlines
📚 Introduction to Gas Laws and Pressure
This paragraph introduces the concept of pressure in the context of gas laws, defining it as force per unit area. It explains the relationship between different units of pressure such as pascals, atmospheres, and millimeters of mercury. The ideal gas law equation (PV=nRT) is introduced, emphasizing the importance of consistent units, particularly liters for volume and kelvin for temperature. The paragraph also touches on the conversion between Celsius and Fahrenheit temperatures.
📈 Boyle's Law: Pressure and Volume Relationship
Boyle's Law is discussed, which describes the inverse relationship between the pressure and volume of a gas at constant temperature and moles. The law is represented by the equation P1V1 = P2V2. The concept is illustrated with an example where the volume of a gas container is tripled, resulting in the pressure being reduced by a factor of three. The paragraph explains that as gas molecules have more space, they collide less frequently with the container walls, leading to reduced pressure.
🌡️ Charles's Law: Volume and Temperature
Charles's Law is introduced, which shows the direct proportionality between the volume of a gas and its temperature when pressure and moles are constant. The law is represented by the equation V1/T1 = V2/T2. The paragraph explains that if the temperature of a gas is doubled, the volume will also double. It also clarifies that volume measurements can be in milliliters or liters, but temperature must be in kelvin for this law to apply correctly.
🌡️ Gay-Lussac's Law: Pressure and Temperature
Gay-Lussac's Law is explained, focusing on the direct relationship between the pressure of a gas and its temperature when volume and moles are held constant. The law is represented by the equation P1/T1 = P2/T2. The paragraph describes how increasing the temperature of a gas leads to an increase in the average kinetic energy of the gas molecules, resulting in more frequent collisions with the container walls and thus an increase in pressure. The concept is illustrated with a scenario involving a balloon expanding due to increased internal pressure from temperature rise.
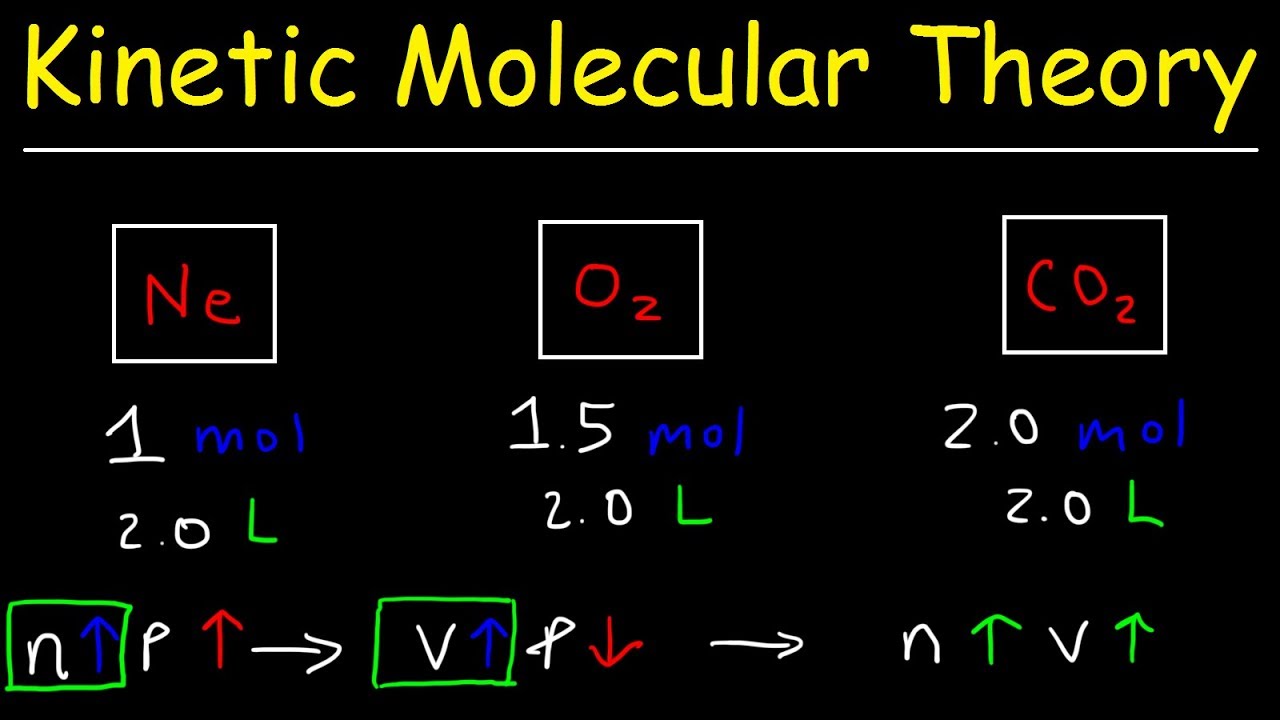
🎈 Avogadro's Law and Gas Density
Avogadro's Law is introduced, which relates the volume of a gas to the number of moles when pressure and temperature are constant. The law is represented by the equation V1/n1 = V2/n2. The paragraph explains that increasing the moles of gas in a container will increase its volume if the container is expandable. The concept of gas density is also discussed, defined as mass per unit volume, with a practical equation derived from the ideal gas law for calculating density based on mass, volume, and molar mass.
🔬 STP and Molar Volume
The concept of Standard Temperature and Pressure (STP) is explained, with a standard temperature of 273 Kelvin and a standard pressure of 1 atm. The paragraph details that at STP, one mole of any ideal gas occupies a volume of 22.4 liters. The derivation of this molar volume from the ideal gas law equation is outlined, using the constants and values specific to STP conditions.
📊 Gas Laws and Their Applications
This paragraph continues the discussion on gas laws, focusing on the practical applications and interrelationships between Boyle's Law, Charles's Law, and Gay-Lussac's Law. It explains how changes in temperature affect the volume and pressure of a gas, and how these changes lead to gas expansion or contraction. The concept of a gas law equilibrium is introduced, where internal and external forces balance out, resulting in no further change in volume.
🌬️ Understanding Gas Density and Its Factors
The factors affecting gas density are explored, including the effects of pressure, molar mass, and temperature on density. The relationship between density and these factors is quantified using equations derived from the ideal gas law. The paragraph also discusses how changes in volume affect density and how Dalton's Law of Partial Pressures relates to the overall pressure exerted by a mixture of gases.
📈 Calculating Mole Fraction and Partial Pressure
The concept of mole fraction is introduced as a way to express the proportion of a particular gas in a mixture. The relationship between mole fraction and partial pressure is explained, with examples provided to illustrate how to calculate these values for different gases in a mixture. The importance of the sum of mole fractions equaling one for a mixture is emphasized, as well as the calculation of partial pressures based on mole fractions and total pressure.
🚀 Root Mean Square Velocity and Gas Behavior
The concept of root mean square velocity is introduced, explaining its derivation from the average kinetic energy of gas particles. The relationship between temperature, molar mass, and the speed of gas molecules is quantified using mathematical equations. The paragraph discusses how changes in temperature and molar mass affect the velocity of gas molecules, with examples provided to illustrate these relationships.
🌀 Graham's Law of Effusion and Gas Properties
Graham's Law of Effusion is introduced, which relates the rate of effusion of a gas to its molar mass. The law is derived from the root mean square velocity equation and discussed in the context of how lighter gases effuse more quickly than heavier ones. The practical application of this law is illustrated with a comparison between hydrogen and oxygen gases, showing how the rate of effusion changes with molar mass.
📊 Gas Density at STP and Molar Mass
The final paragraph discusses the calculation of gas density at Standard Temperature and Pressure (STP), providing a straightforward equation for determining the density of a gas based on its molar mass. The relationship between gas density and molar mass at STP is highlighted, with a specific example given for oxygen gas. The summary emphasizes the practical use of this information in understanding gas behavior under standard conditions.
Mindmap
Keywords
💡Pressure
💡Pascal
💡Ideal Gas Law
💡Gas Constant
💡Moles
💡Kelvin
💡Boyle's Law
💡Charles's Law
💡Avogadro's Law
💡Density
💡STP (Standard Temperature and Pressure)
💡Dalton's Law of Partial Pressures
Highlights
Pressure is defined as force divided by area, with units of Pascal (Pa) being the standard unit of pressure.
One atmosphere (atm) is equivalent to 760 torr or 101.3 kilopascals (kPa), which are common units of pressure in chemistry.
The ideal gas law equation is PV = nRT, where P is pressure, V is volume, n is moles, R is the gas constant, and T is temperature in Kelvin.
The gas constant R has different values depending on the units used; 0.08206 L·atm/(mol·K) when using liters, atmospheres, moles, and Kelvin.
Temperature must be converted to Kelvin by adding 273.15 to the Celsius temperature, or using the equation (°F + 32) × 5/9 = °C.
Boyle's Law states that at constant temperature and moles, the volume of a gas is inversely proportional to its pressure (P1V1 = P2V2).
Charles's Law indicates that at constant pressure and moles, the volume of a gas is directly proportional to its temperature (V1/T1 = V2/T2).
Gay-Lussac's Law describes that at constant volume and moles, the pressure of a gas is directly proportional to its temperature (P1/T1 = P2/T2).
Avogadro's Law states that at constant pressure and temperature, the volume of a gas is directly proportional to the number of moles (V1/n1 = V2/n2).
At standard temperature and pressure (STP), one mole of any ideal gas occupies a volume of 22.4 liters.
Gas density is calculated as mass over volume, typically reported in grams per liter (g/L).
The density of a gas at STP can be found using the equation: Density = Molar Mass / 22.4.
Dalton's Law of Partial Pressures states that the total pressure of a gas mixture is equal to the sum of the partial pressures of its individual components.
Mole fraction is the fraction of a particular gas in a mixture, calculated as the partial pressure divided by the total pressure, and the sum of all mole fractions equals one.
The root mean square velocity of a gas can be calculated using the equation: v_rms = √(3RT/M), where R is the gas constant, T is the temperature in Kelvin, and M is the molar mass in kilograms per mole.
Graham's Law of Effusion relates the rate of effusion of a gas to its molar mass, stating that the rate of effusion is inversely proportional to the square root of the molar mass.
Understanding the relationships between pressure, volume, temperature, and moles is crucial for predicting the behavior of gases in various conditions.
The ideal gas law and its derived laws are fundamental for explaining the behavior of gases and have wide applications in chemistry and physics.
Transcripts
Browse More Related Video

Gas Law Problems Combined & Ideal - Density, Molar Mass, Mole Fraction, Partial Pressure, Effusion

Ideal Gas Problems: Crash Course Chemistry #13

9.3 Additional Gas Laws | Dalton's Law and Graham's Law | High School Chemistry

9.2 Gas Laws including the Ideal Gas Law | High School Chemistry
Kinetic Molecular Theory of Gases - Practice Problems

Ideal Gas Law
5.0 / 5 (0 votes)
Thanks for rating: