Kinetic Energy

Bozeman Science
13 Feb 201504:46
EducationalLearning
32 Likes 10 Comments

TLDRIn this insightful video, Mr. Andersen explores the nuances of kinetic and potential energy, clarifying that while objects in motion or rotation possess kinetic energy, potential energy requires the interaction with another object or system. He uses the example of a baseball to illustrate how its kinetic energy is calculated and demonstrates through a pendulum simulation how removing the Earth eliminates potential energy, emphasizing that isolated objects lack potential energy due to the absence of a gravitational field or other forces.

Takeaways
  • πŸƒ Kinetic energy is the energy of motion; an object with mass and velocity possesses it.
  • πŸ”„ Rotational kinetic energy is the energy due to an object's rotation, using angular velocity instead of linear velocity.
  • βš™οΈ An object in isolation cannot have potential energy; it requires interaction with another object or the system.
  • 🌍 For example, the Earth's gravitational field is necessary for an object to have gravitational potential energy.
  • πŸ“ The formula for kinetic energy is KE = 1/2 * m * v^2, where m is mass and v is velocity.
  • πŸ”„ The formula for rotational kinetic energy is KE = 1/2 * I * Ο‰^2, with I being the moment of inertia and Ο‰ the angular velocity.
  • πŸ“ˆ Potential energy can be in the form of gravitational or electric potential energy, depending on the context.
  • 🌐 Removing the Earth from a system, such as in a pendulum model, results in the loss of potential energy.
  • πŸ“ When pitching a baseball, it has both translational (linear) and rotational (angular) kinetic energy.
  • πŸ”’ To calculate the kinetic energy of a baseball pitched at 90 mph, use the given mass and velocity values in the formula.
  • πŸ’‘ Understanding the distinction between kinetic and potential energy, and how they relate to the presence of other objects or systems, is crucial.
Q & A

  • What is kinetic energy?

    -Kinetic energy is the energy of motion. An object with mass and velocity possesses kinetic energy.

  • How is rotational kinetic energy different from linear kinetic energy?

    -Rotational kinetic energy is associated with an object's rotation, using angular velocity and moment of inertia instead of linear velocity and mass.

  • What is the equation for calculating linear kinetic energy?

    -The equation for linear kinetic energy is KE = 1/2 * m * v^2, where m is mass and v is velocity.

  • What is the equation for calculating rotational kinetic energy?

    -The equation for rotational kinetic energy is KE = 1/2 * I * Ο‰^2, where I is rotational inertia and Ο‰ is angular velocity.

  • Can an object have potential energy in isolation?

    -No, an object in isolation cannot have potential energy. Potential energy requires the presence of another object or a system to be stored due to position.

  • What happens to a pendulum's potential energy when the earth is removed from the simulation?

    -Without the earth, the pendulum does not have any potential energy because there is no gravitational field to store potential energy.

  • How can electric potential energy be converted into kinetic energy?

    -By adding other objects, the electric potential energy can be converted into kinetic energy through interactions between charged particles.

  • How much kinetic energy does a baseball have when pitched at 90 miles per hour?

    -A 90 mph pitch (which is 41 m/s) of a 145-gram baseball results in approximately 120 joules of kinetic energy.

  • What are the two types of kinetic energy a pitched baseball has?

    -A pitched baseball has both translational kinetic energy (due to its motion through space) and rotational kinetic energy (due to its spin).

  • How can you calculate the rotational kinetic energy of an object?

    -You can calculate rotational kinetic energy by knowing the object's moment of inertia (I) and its angular velocity (Ο‰), then using the formula KE = 1/2 * I * Ο‰^2.

  • What is the significance of the PHET simulation in understanding potential and kinetic energy?

    -The PHET simulation demonstrates the conversion between potential and kinetic energy, showing how removing the earth (and gravity) affects the potential energy storage of a pendulum.

Outlines
00:00
🌟 Introduction to Kinetic Energy

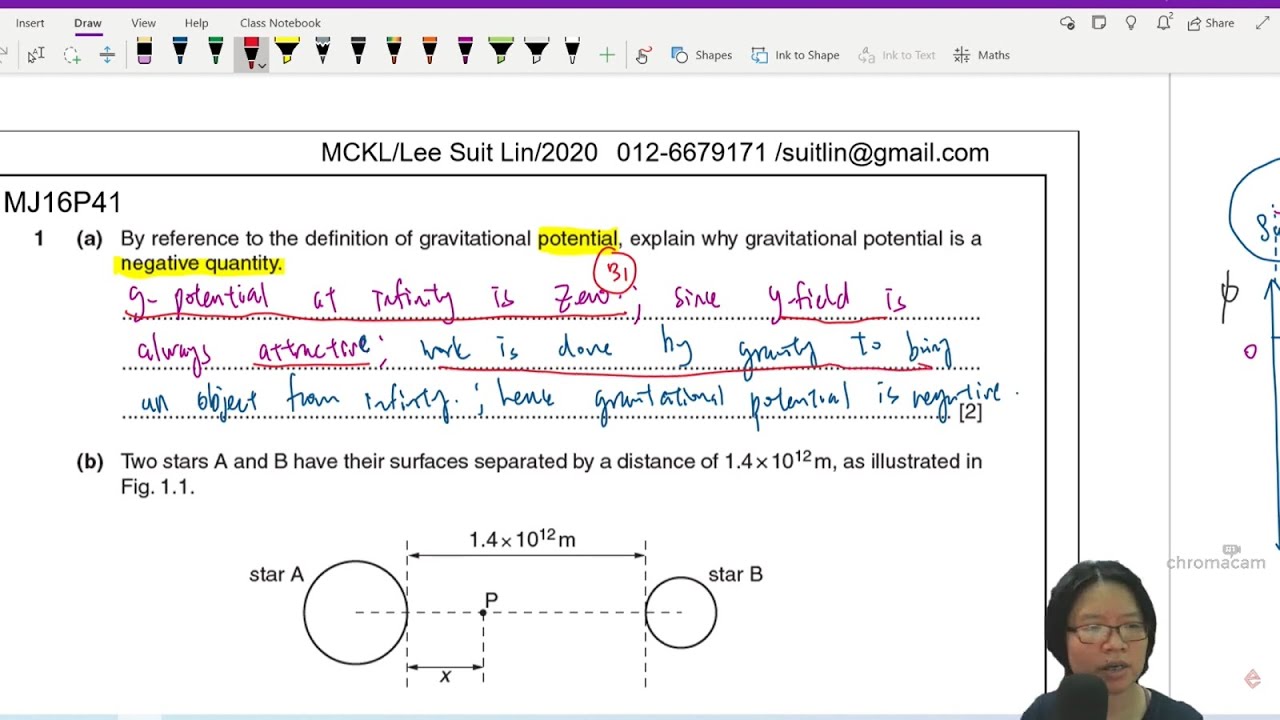
This paragraph introduces the concept of kinetic energy, explaining it as the energy of motion. It addresses the question of why kinetic energy is being discussed at this stage of the course and highlights the subtleties between kinetic and potential energy. The explanation includes the conditions under which an object possesses kinetic energy, whether it's moving linearly or rotating, and introduces the formula for calculating kinetic energy (1/2 mv^2). The paragraph also touches on the absence of potential energy in isolated objects and the necessity of another object or system for potential energy to exist.

Mindmap
Keywords
πŸ’‘Kinetic Energy
Kinetic energy is the energy of motion. It is possessed by an object due to its mass and velocity. In the context of the video, it is explained that any object with mass and velocity has kinetic energy, which can be calculated using the formula KE = 1/2 mv^2, where m is mass and v is velocity. The video also differentiates between linear kinetic energy (associated with the object's velocity) and rotational kinetic energy (associated with angular velocity and rotational inertia).
πŸ’‘Potential Energy
Potential energy is the stored energy of an object due to its position or condition. In classical physics, an object by itself does not have potential energy; it requires the presence of another object or a system, such as the Earth's gravitational field, to have potential energy. The video explains that potential energy can be converted into kinetic energy and vice versa, as demonstrated by a pendulum's oscillation between potential and kinetic energy states.
πŸ’‘Angular Velocity
Angular velocity is the rate at which an object rotates around a fixed axis or pivot. It is measured in radians per second. In the video, angular velocity is used in the calculation of rotational kinetic energy, which is different from linear kinetic energy as it pertains to an object's spinning motion rather than its linear motion.
πŸ’‘Moment of Inertia
The moment of inertia, also known as rotational inertia, is a measure of an object's resistance to rotational motion about a particular axis. It depends on both the mass of the object and the distribution of that mass relative to the axis of rotation. In the video, the moment of inertia is a key factor in calculating rotational kinetic energy using the formula KE = 1/2 I Ο‰^2, where I is the moment of inertia and Ο‰ is the angular velocity.
πŸ’‘Gravitational Field
A gravitational field is the region around a massive object where its gravitational force affects other objects. In the video, the Earth's gravitational field is mentioned as a necessary condition for an object to have gravitational potential energy. The presence of the gravitational field allows for the conversion of potential energy into kinetic energy and back as the object moves within the field.
πŸ’‘Electric Potential Energy
Electric potential energy is the stored energy of an electric charge in an electric field due to its position relative to other charges. In the video, it is mentioned as another form of potential energy that can be converted into kinetic energy when other objects are present to create the electric field.
πŸ’‘PhET Simulation
PhET simulations are interactive science and math simulations used for education, created by the University of Colorado Boulder. In the video, a PhET simulation is used to visually demonstrate the concepts of kinetic and potential energy, particularly how potential energy is dependent on the presence of a system or another object.
πŸ’‘Translational Kinetic Energy
Translational kinetic energy refers to the energy an object possesses due to its linear motion. It is directly related to the object's mass and the square of its velocity. In the video, translational kinetic energy is discussed as a type of kinetic energy that is present when an object moves in a straight line, as opposed to rotational kinetic energy which is associated with spinning motion.
πŸ’‘Rotational Kinetic Energy
Rotational kinetic energy is the energy an object has due to its rotational motion around an axis. It is calculated using the formula KE = 1/2 I Ο‰^2, where I is the moment of inertia and Ο‰ is the angular velocity. In the video, rotational kinetic energy is emphasized as a form of kinetic energy that is distinct from linear motion and is related to the object's spinning motion.
πŸ’‘Significant Digits
Significant digits are the digits in a number that carry meaning contributing to its precision. This concept is important in scientific calculations to ensure that the results are accurately represented without implying a false sense of precision. In the video, significant digits are mentioned in the context of calculating the kinetic energy of the spinning baseball, emphasizing the importance of reporting only the necessary digits to convey the correct magnitude of the value.
Highlights

Kinetic energy is the energy of motion, which an object possesses due to its mass and velocity.

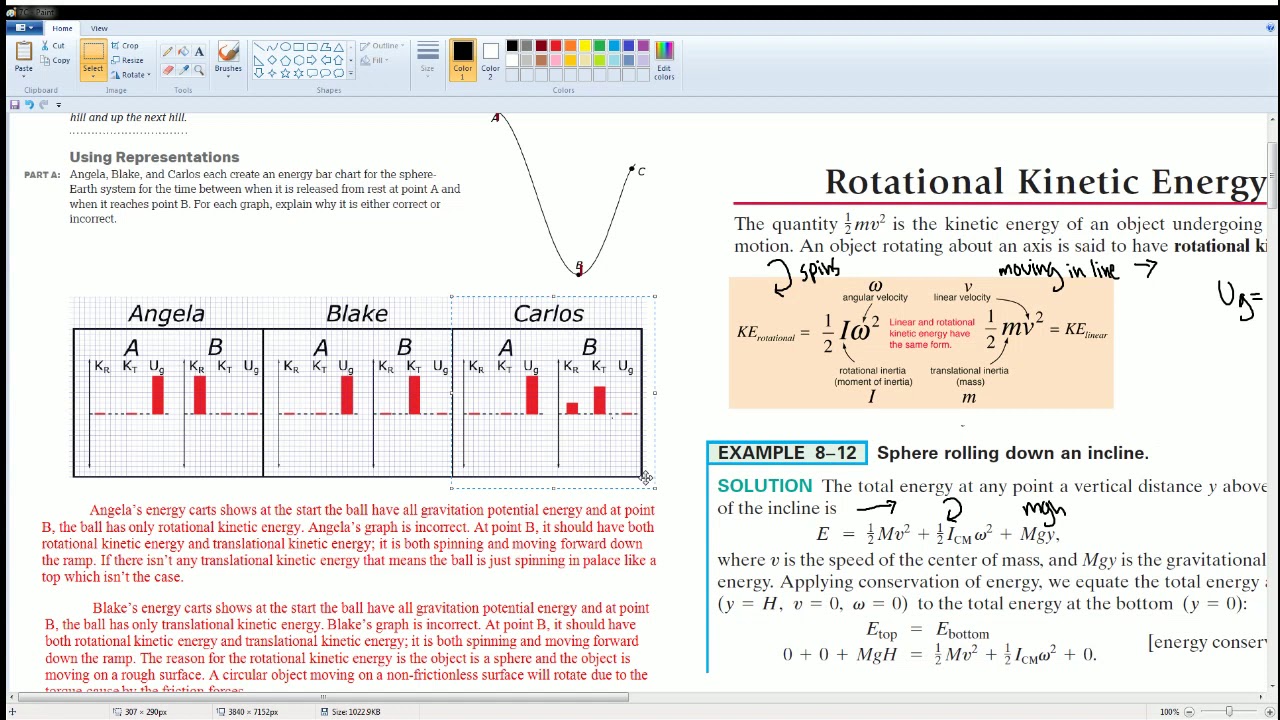
Rotational kinetic energy is the energy associated with an object's rotation, using angular velocity instead of linear velocity.

An object in isolation does not have potential energy; it requires another object or a system for potential energy to exist.

The equation for kinetic energy is KE = 0.5 * m * v^2, where m is mass and v is velocity.

For rotational kinetic energy, the equation is KE = 0.5 * I * Ο‰^2, with I being the moment of inertia and Ο‰ the angular velocity.

Potential energy can be gravitational or electric, depending on the nature of the interaction between objects.

A pendulum demonstrates the conversion between potential and kinetic energy when oscillating back and forth.

Removing the Earth from the simulation eliminates potential energy, leaving only kinetic energy.

When the Earth is reintroduced, potential energy is added back into the system, allowing for the conversion between potential and kinetic energy.

An object's potential energy is related to its position within a system and the forces acting upon it.

Calculating the kinetic energy of a baseball pitched at 90 miles per hour involves using its mass and velocity.

A spinning baseball has both translational kinetic energy and rotational kinetic energy.

Understanding the difference between kinetic and potential energy is crucial for grasping fundamental physics concepts.

The video uses a PHET simulation to visually demonstrate the concepts of kinetic and potential energy.

The relationship between mass, velocity, and kinetic energy is fundamental to understanding the behavior of moving objects.

The moment of inertia and angular velocity are key factors in calculating the rotational kinetic energy of an object.

The video emphasizes the importance of considering the entire system when discussing potential energy.

Transcripts

Browse More Related Video

Kinetic Energy and Potential Energy

Kinetic Energy and Potential Energy

Total Energy

MJ16 P41 Q1 Gravitational Potential Between 2 Stars | A2 G-fields | Cambridge A Level 9702 Physics

The Difference Between Kinetic and Potential Energy

AP Physics Workbook 7.C Rotational Energy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationKineticEnergyPotentialEnergyAngularVelocityMechanicalEnergyGravitationalFieldPhETSimulationBaseballPitchEnergyConversionClassicalPhysics