Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (68 of 92) What is the Wave Number k=?

Michel van Biezen
27 Apr 201803:33
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of wave number (K), clarifying its definition as the number of radians per unit distance and its relation to wavelength. It explains how K is calculated by dividing 2π radians by the wavelength (λ), and further connects K to the momentum of a particle through Planck's constant (h-bar). The script illustrates that a lower wave number corresponds to a longer wavelength, using the example of particles approaching a step potential to demonstrate this relationship. Overall, the video aims to demystify wave number and its significance in wave physics.

Takeaways
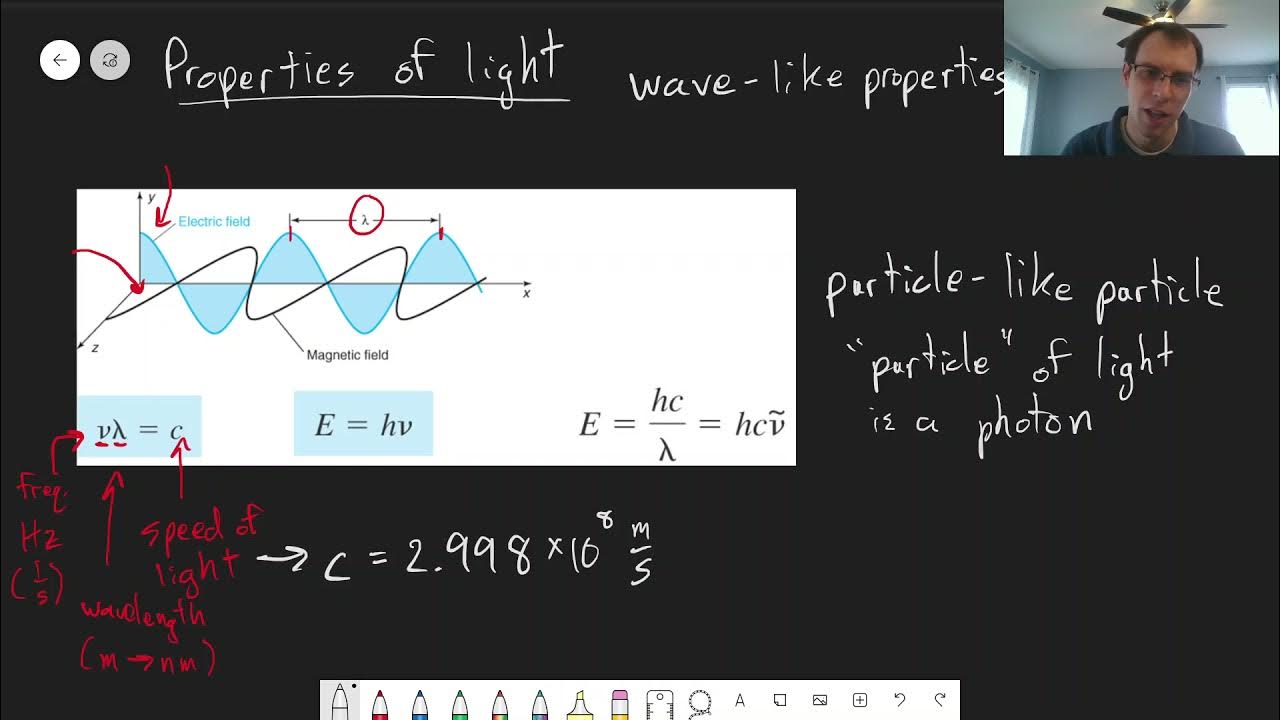
  • 🌊 Wave number (K) is defined as the number of radians per unit distance in a wave.
  • 📏 Wavelength is equivalent to 360 degrees or 2π radians, which relates to the wave number.
  • 🔢 K is calculated as 2π radians divided by the wavelength (λ) in meters.
  • 📐 For a wave with a 4-meter wavelength, K equals π/2 radians per meter.
  • 🌀 The wave number indicates the number of radians per meter, which corresponds to the wave's wavelength.
  • 💫 K can also be seen as the momentum of a particle divided by h-bar (ħ), where h is Planck's constant.
  • 🌱 As the wave number (K) decreases, the wavelength (λ) increases, and vice versa.
  • 🎲 The wave number's change can be observed in quantum mechanics, such as in a particle approaching a step potential.
  • 📈 A smaller wave number (K) results in a larger wavelength, which can affect particle transmission.
  • 🔄 The relationship between wave number and wavelength is fundamental to understanding wave-particle duality.
  • 📚 Understanding wave number is crucial for grasping various concepts in physics, including quantum mechanics.
Q & A

  • What is the definition of wave number (K)?

    -The wave number (K) is defined as the number of radians per unit distance in a wave.

  • How is the wave number related to the wavelength?

    -The wave number (K) is inversely proportional to the wavelength. It can be calculated as 2π radians divided by the wavelength (λ) in meters.

  • What does a wavelength of 360 degrees or 2π radians signify?

    -A wavelength of 360 degrees or 2π radians signifies a full circle or a complete cycle of the wave.

  • How can one calculate the wave number for a wave with a wavelength of 4 meters?

    -For a wave with a wavelength of 4 meters, the wave number (K) would be calculated as 2π divided by 4, which equals π/2 radians per meter.

  • What is the significance of the relationship between wave number and momentum in quantum mechanics?

    -In quantum mechanics, the wave number (K) can be defined as the momentum (p) of a particle divided by h-bar (ħ), which is Planck's constant divided by 2π. This relationship connects the wave-like properties of particles with their momentum.

  • How does the wave number affect the wavelength of a particle?

    -As the wave number decreases, the wavelength increases. This means that a smaller wave number corresponds to a larger wavelength for a particle.

  • What happens to the wave number when a particle transitions from one region to another with a different potential?

    -When a particle transitions from one region to another, the wave number (K) on the right side will be smaller than on the left side if the particle is transmitted through a step potential.

  • What is the de Broglie wavelength?

    -The de Broglie wavelength (λ) of a particle is given by the Planck's constant (h) divided by the product of 2π and the particle's momentum (p), represented as λ = h / (2πp). It describes the wavelength associated with a particle in quantum mechanics.

  • How can one determine the wavelength of a particle knowing its momentum?

    -The wavelength of a particle can be determined by the formula λ = h / (MV), where h is Planck's constant, M is the mass of the particle, and V is its velocity.

  • What is the implication of a smaller wave number in the context of wave propagation?

    -A smaller wave number implies a larger wavelength, which means that the wave covers more spatial extent per cycle as it propagates.

  • How does the concept of wave number help in understanding wave behavior?

    -The concept of wave number helps in understanding the spatial frequency of waves, which is the number of cycles that occur over a certain distance. It provides insight into how waves with different wavelengths interact with their environment and other waves.

Outlines
00:00
🌊 Introduction to Wave Number

This paragraph introduces the concept of wave number (K), acknowledging its complexity and historical difficulty in understanding. It explains that wave number is defined as the number of radians per unit distance and relates this to the wavelength of a wave, which is equivalent to 360 degrees or 2π radians. The explanation continues with a practical example, showing how to calculate K for a wave with a wavelength of 4 meters, and further discusses the relationship between wave number and momentum of a particle, introducing the concept of de Broglie wavelength.

Mindmap
Keywords
💡Wave Number (K)
Wave number, denoted as K, is a fundamental concept in wave physics, defined as the number of radians per unit distance. It is central to the video's theme as it helps in understanding the relationship between the wavelength of a wave and its spatial properties. The script uses the example of a wave with a wavelength of 4 meters to illustrate that K equals pi over 2 radians per meter, indicating that for every meter, there is half a radian of wave phase change.
💡Wavelength
Wavelength is the spatial distance between two consecutive points in phase on a wave, typically one full cycle. It is crucial in the video as it is directly related to the wave number. The wavelength is also equated to 360 degrees or 2 pi radians, which helps in understanding the wave number as the ratio of the circle's circumference (2 pi radians) to its length (in meters).
💡Radians
Radians are a unit of angular measure used to describe the angle subtended at the center of a circle by an arc. In the context of the video, radians are used to define the wave number, as they relate to the angular displacement per unit length along the wave. The wave number is the number of radians associated with each unit length of the wave, which is crucial for understanding wave behavior.
💡Momentum
Momentum in physics is the product of an object's mass and its velocity. In the video, momentum is related to the wave number through the concept of de Broglie wavelength, which states that the wavelength of a particle is inversely proportional to its momentum. This relationship is pivotal as it connects the particle-like properties of a wave, as described by the wave number, to its momentum.
💡h-bar (h/2 pi)
h-bar, represented as h/2 pi, is a constant in quantum mechanics known as the reduced Planck constant. It is used in the calculation of the de Broglie wavelength, which relates the wave-like properties of particles to their momentum. In the video, h-bar is integral to understanding how the wave number is connected to the momentum of particles.
💡de Broglie Wavelength
The de Broglie wavelength is a concept in quantum mechanics that describes the wavelength associated with a particle in motion. It is inversely proportional to the particle's momentum, which is a key concept in the video. The de Broglie wavelength is used to explain how the wave number is related to the properties of particles, such as electrons, in quantum mechanics.
💡Step Potential
A step potential is a type of potential energy barrier that changes abruptly at a certain position, creating a 'step' in the potential energy diagram. In the video, it is used as an example to illustrate how the wave number changes when a particle encounters such a barrier, leading to a change in wavelength as it moves from one region to another.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video touches on quantum mechanics by discussing the wave number in relation to the de Broglie wavelength and the momentum of particles, emphasizing the wave-particle duality concept.
💡Wave-Particle Duality
Wave-particle duality is a core concept in quantum mechanics that states that particles can exhibit both wave-like and particle-like properties. The video explores this duality by explaining how the wave number is related to the momentum and wavelength of particles, showing that the behavior of particles can be described in terms of waves.
💡Planck's Constant (h)
Planck's constant is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. In the video, Planck's constant is used in the context of calculating the de Broglie wavelength and understanding the relationship between the wave number and the momentum of particles.
💡Radiance
Radiance is a term used in physics to describe the amount of light or electromagnetic radiation that is emitted, reflected, or received by a surface or volume per unit solid angle, area, and wavelength. Although not explicitly mentioned in the video, the concept of radiance could be related to the wave nature of light and how it interacts with matter, which is a topic in the broader context of wave physics.
Highlights

The lecture focuses on explaining the concept of wave number, which can be confusing.

Wave number (K) is defined as the number of radians per unit distance.

Wavelength is equivalent to 360 degrees or 2 pi radians.

The relationship between wavelength and wave number is derived by dividing the wavelength by 2 pi radians.

For a wave with a wavelength of 4 meters, the wave number K is calculated as pi over 2 radians per meter.

Wave number can also be understood as the momentum of a particle divided by h-bar.

The momentum is represented as M times V, where M is the mass and V is the velocity.

h-bar is defined as Planck's constant divided by 2 pi.

The wavelength of a particle can be defined as h-bar divided by the momentum (h/MV).

As the wave number decreases, the wavelength increases.

A smaller wave number corresponds to a larger wavelength.

In the context of a particle approaching a step potential, a decrease in wave number results in an increase in wavelength.

The wave number is fundamental in understanding wave behavior and particle transmission.

The concept of wave number is central to wave-particle duality and quantum mechanics.

The lecture provides a clear and detailed explanation of wave number, its calculation, and its significance.

The wave number is a key parameter in the study of wave phenomena and quantum mechanics.

Understanding wave number helps in the application of wave-particle duality principles in various scientific fields.

The lecture elucidates the connection between wave number, wavelength, and the behavior of particles in different potentials.

The wave number is a measure of how many radians are contained in a given distance, which is crucial for wave analysis.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (19 of 92) Particle in 1-D Box: Example 1/2

Chapter 18: Properties of Light | CHM 214 | 150

Wave Equation

19. Waves

Grade 10 Physics Wave Speed

Exam Transverse Waves Grade 10

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Wave NumberPhysics LectureWavelength RelationParticle MomentumMathematical AnalysisEducational ContentQuantum MechanicsWave PhenomenaOnline LearningPhysics Concepts