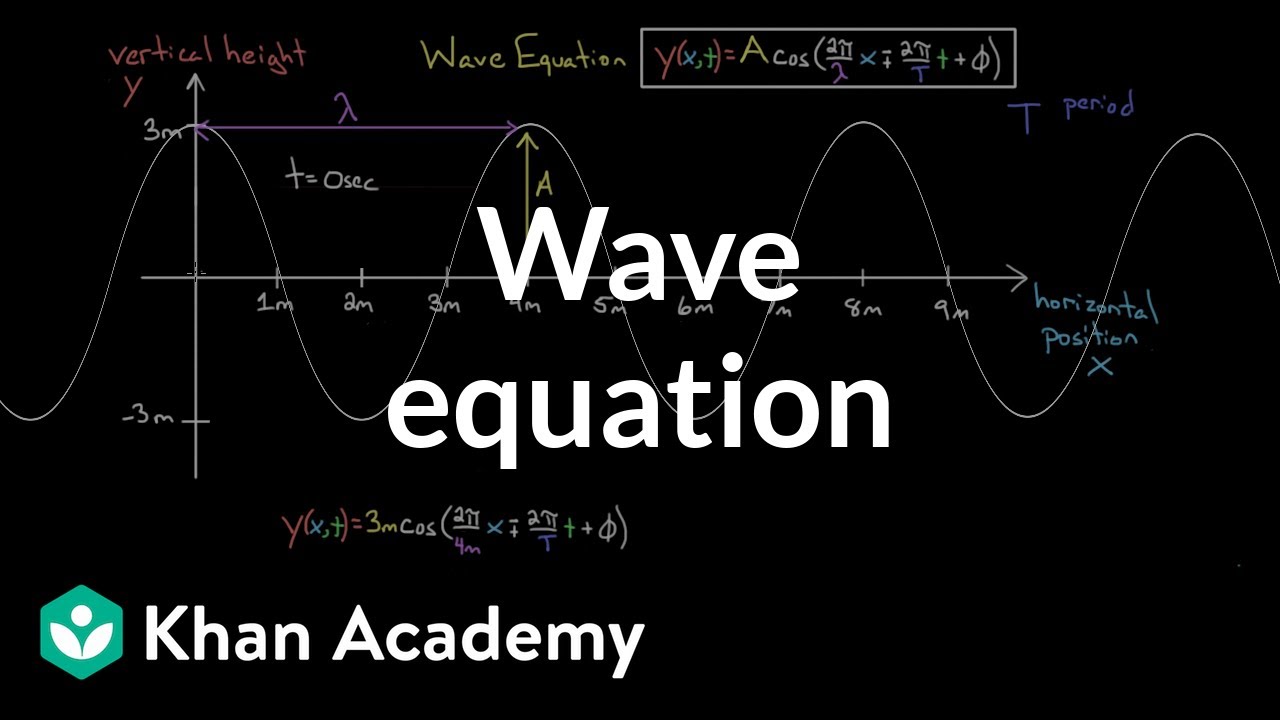
Wave Equation
TLDRThis video script delves into the physics of the wave equation for a traveling sinusoidal wave, elucidating its components and constants such as amplitude (A), angular wave number (k), angular frequency (ω), and phase (φ). It emphasizes the importance of units, explaining how each variable contributes to the overall unit of the equation, which is radians for the vertical position (y). The script clarifies common symbol confusions and provides a clear understanding of how these elements interplay in the wave equation, ultimately resulting in a dimensionless sine function.
Takeaways
- 🌊 The wave equation discussed is for a traveling sinusoidal wave, representing the vertical position as a function of horizontal position and time.
- 📍 The vertical position 'y' is dependent on 'x' (horizontal position) and 't' (time), aiming to find the wave's position at a given time and place.
- 🔍 Problem-specific constants include amplitude 'A', phase 'phi', angular frequency 'omega', and angular wave number 'k', each crucial for wave description.
- 📏 Amplitude 'A' is the maximum displacement of the wave and can be measured in various distance units like meters, centimeters, or feet.
- 🌀 The angular wave number 'k' is distinct from the spring constant and is related to the wavelength, measured in radians per meter.
- 🔄 Angular frequency 'omega' is associated with the wave's period and is measured in radians per second, reflecting rotational properties.
- 🕰 The phase 'phi' indicates the starting point of oscillations and ranges between 0 and 2π radians, also measured in radians.
- 🔢 In the wave equation, units of 'k' (radians per meter), 'x' (meters), 'omega' (radians per second), and 'phi' (radians) are involved, with meters and seconds canceling out.
- 📉 After unit cancellation, the sine function in the equation operates on a dimensionless quantity in radians, resulting in a unitless value.
- 📈 The vertical position 'y' of the wave will share the unit of the amplitude, typically meters but could be any length unit.
- 📚 Understanding the wave equation requires attention to the units and constants involved, ensuring calculations are performed in radian mode for angular measurements.
Q & A
What is the standard equation for a traveling sinusoidal wave in physics?
-The standard equation for a traveling sinusoidal wave is a function that describes the vertical position (y) as a function of horizontal position (x) and time (t), incorporating amplitude (A), phase (phi), angular frequency (omega), and angular wave number (k).
What does the variable 'y' in the wave equation represent?
-In the wave equation, 'y' represents the vertical position of the wave at a particular point along the horizontal position (x) at a given time (t).
What are the problem-specific constants in the wave equation?
-The problem-specific constants in the wave equation include amplitude (A), phase (phi), angular frequency (omega), and angular wave number (k).
What is the amplitude 'A' in the wave equation?
-The amplitude 'A' is the maximum displacement of the oscillator in the wave and can be measured in any distance units, such as meters, centimeters, or feet.
What is the symbol for the angular wave number and what is its unit?
-The symbol for the angular wave number is 'k', and its unit is radians per meter.
What is the difference between the angular wave number 'k' and the spring constant 'k'?
-The angular wave number 'k' is related to the wavelength of the wave and has units of radians per meter, whereas the spring constant 'k' is a different physical quantity related to the stiffness of a spring.
What does the angular frequency 'omega' represent and what are its units?
-The angular frequency 'omega' represents the rotational property of the wave and is related to the period of the wave. Its units are radians per second.
What is the phase 'phi' and what does it measure?
-The phase 'phi', represented by the Greek letter phi, measures where the oscillations started in the cycle and can range between 0 and 2 pi radians.
How do the units of the angular wave number and the angular frequency affect the units of the vertical position 'y'?
-The units of the angular wave number (radians per meter) and the angular frequency (radians per second), along with the horizontal position in meters and time in seconds, result in the vertical position 'y' having the same units as the amplitude, typically meters, but it could be any length measurement.
Why is it important for the calculator to be in radian mode when calculating the sine of an angle in the wave equation?
-It is important for the calculator to be in radian mode because the sine function requires the input angle to be in radians, which is the unit for the phase constant and angular frequency in the wave equation.
Is there a unit associated with the sine of an angle in the wave equation?
-No, the sine of an angle is a dimensionless, unitless quantity. The units for the vertical position 'y' come from the amplitude 'A'.
Outlines
🌊 Introduction to the Wave Equation
The script introduces the wave equation used in physics to describe a traveling sinusoidal wave. It explains the variables involved, including the vertical position (y) as a function of horizontal position (x) and time (t), and the problem-specific constants such as amplitude (A), phase (phi), angular frequency (omega), and angular wave number (k). The amplitude represents the maximum displacement, and the angular wave number and frequency are related to the wavelength and period of the wave, respectively. The phase is described as a measure of where the oscillations start in the cycle, with values ranging from 0 to 2 pi radians. The units for these quantities are also discussed, emphasizing that the angular wave number and frequency must be in radians per meter and radians per second, respectively, while the phase is in radians. The explanation concludes with an overview of how these units interact within the wave equation, resulting in a dimensionless quantity after the sine function is applied.
Mindmap
Keywords
💡Wave Equation
💡Vertical Position (y)
💡Horizontal Position (x)
💡Time Variable (t)
💡Amplitude (A)
💡Phase (phi)
💡Angular Wave Number (k)
💡Angular Frequency (omega)
💡Wavelength
💡Units
💡Sine Function
Highlights
Introduction to the wave equation and its significance in physics for describing traveling sinusoidal waves.
Explanation of the variables in the wave equation: vertical position y as a function of horizontal position x and time t.
Introduction of problem-specific constants in the wave equation: amplitude A, phase phi, angular frequency, and angular wave number k.
Clarification of the amplitude A as the maximum displacement of the oscillator, with a focus on using capital A to avoid confusion with lowercase a.
Amplitude A can be measured in various distance units such as meters, centimeters, or feet.
Differentiation between the angular wave number k and the spring constant k, emphasizing that they are distinct variables.
Angular wave number k is related to the wavelength and must be in units of radians per meter.
Angular frequency omega is related to the period of the wave and is measured in radians per second, with a reminder to use the Greek letter omega, not W.
Phase phi, also known as phase shift or phase constant, measures where the oscillations start in the cycle and ranges between 0 and 2 pi radians.
Units of the phase constant phi must be in radians for the equation.
Unit analysis of the wave equation components, showing how meters and seconds cancel out, leaving radians as the overall unit.
Emphasis on the sine calculation requiring radian mode on a calculator and the resulting dimensionless quantity after sine is applied.
The amplitude unit determines the unit of the vertical position y on the wave, which can vary but is typically meters.
Final wave equation summary, highlighting the relationship between the variables and constants and their units.
The importance of understanding the units and dimensions in the wave equation for accurate calculations and interpretations.
The transcript provides a detailed breakdown of the wave equation, making it accessible for learners to grasp the fundamental concepts in wave physics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: