2022 Live Review 7 | AP Calculus BC | Working with Polar Equations
TLDRIn this engaging video, the presenters delve into the intricacies of polar coordinates, a topic that often challenges students in AP Calculus BC. They provide valuable tips and strategies for tackling common problem types, including finding the area between polar curves and converting between polar and rectangular coordinates. The video also humorously reveals the presenter's new tattoo, celebrating their affinity for polar coordinates. The session is filled with practical examples, calculator usage, and insights into the AP exam's expectations, aiming to demystify polar graphs and bolster students' confidence.
Takeaways
- 📚 The session focuses on polar coordinates in the context of the AP Calculus BC exam review, aiming to provide strategies and tips for tackling polar-related problems.
- 🎥 The instructor, Tony Record, is joined by Brian Passwater to discuss various polar coordinate concepts, including area calculations, conversion formulas, and the slope of tangent lines.
- 📊 The video includes several example problems that demonstrate how to calculate the area between polar curves, the use of conversion formulas, and understanding the meaning of r in polar coordinates.
- 🌐 The handouts provided contain additional practice problems and materials that align with the College Board curriculum, specifically Unit 9.7 to 9.9, which is dedicated to parametric and polar functions.
- 🎨 The instructor shares a personal anecdote about getting matching tattoos with his wife related to polar coordinates, highlighting the significance of the subject matter.
- 🤔 The video emphasizes the importance of understanding the conceptual basis behind polar coordinate problems rather than just memorizing formulas, as the AP exam aims to assess comprehension and application of concepts.
- 📈 The session includes a detailed walkthrough of how to set up and calculate the area of a region bounded by polar curves, emphasizing the need to correctly identify limits of integration and the importance of squaring the r value.
- 🔢 The use of a graphing calculator is integral for solving problems involving polar coordinates, and the video provides guidance on how to use the calculator effectively, including finding intersection points and evaluating functions at specific angles.
- 📝 The video provides tips on how to approach multiple-choice and free-response questions on the AP exam, including the strategy of solving problems in stages and the importance of accurate decimal places in answers.
- 🎓 The instructors remind students that while certain trigonometric identities may not be required for the AP exam, a solid understanding of basic trigonometric relationships is still beneficial for college courses.
- 🚀 The video concludes with encouragement for students to continue practicing and reviewing materials, promising a final tips session to help prepare for the AP exam.
Q & A
What is the main topic of discussion in the video?
-The main topic of discussion in the video is polar coordinates in the context of AP Calculus BC, including their applications, common problem types, and strategies for solving related problems.
What is the significance of the speaker's tattoo in relation to the video content?
-The speaker's tattoo, which he plans to reveal at the end of the video, is significant as it is related to polar coordinates, symbolizing his enthusiasm for the topic and serving as a visual representation of the mathematical concepts discussed.
How does the speaker address the common struggles students face with polar coordinates?
-The speaker acknowledges that polar coordinates is a challenging topic for students, but he emphasizes that with practice and the right strategies, students can overcome these difficulties and master the concepts. He plans to provide tips and strategies to help students tackle common problem types in polar coordinates.
What are some key concepts related to polar coordinates discussed in the video?
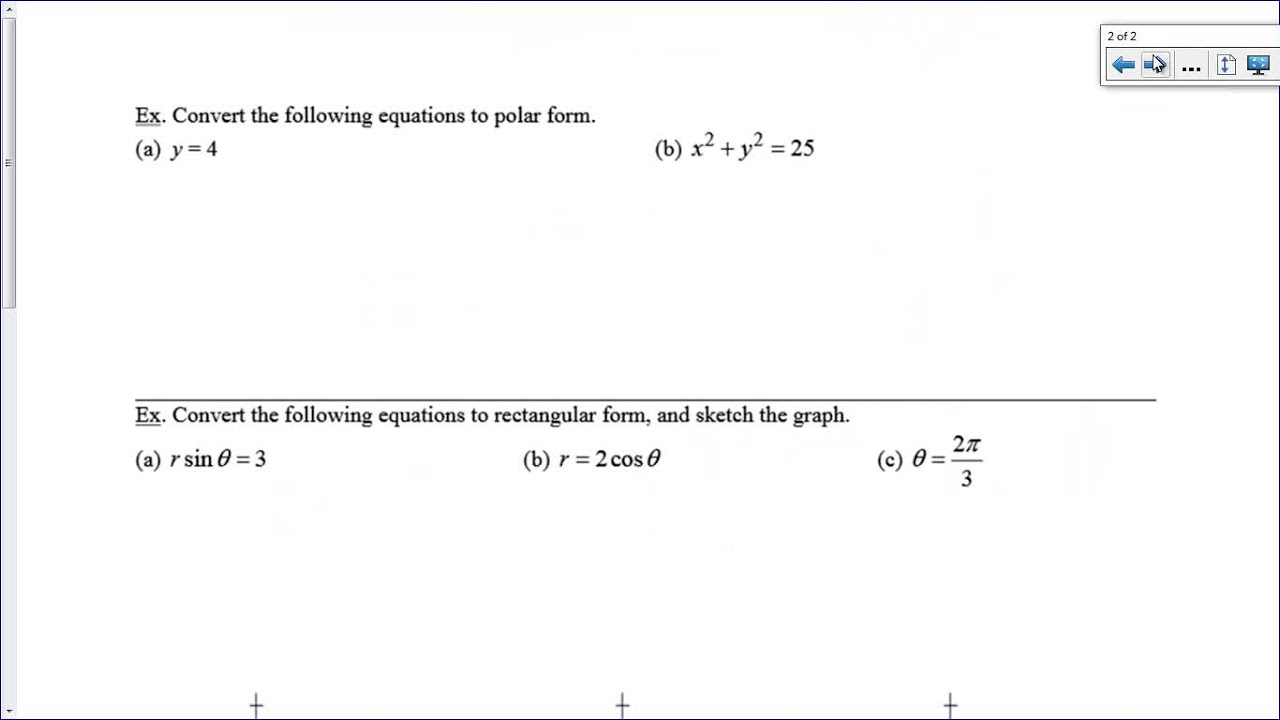
-Some key concepts discussed include finding the area between polar curves, conversion formulas between polar and rectangular coordinates, the slope of a tangent line in polar coordinates (dy/dx = dy/dθ / dx/dθ), and understanding the meaning of r in polar equations.
How does the speaker plan to help students prepare for the AP exam regarding polar coordinates?
-The speaker plans to provide students with handouts containing graphs and additional problems, as well as strategies for solving common problem types. He also discusses the importance of understanding concepts rather than just memorizing formulas, which is a trend in recent AP exams.
What is the significance of the 'magic flashlight' analogy used in the video?
-The 'magic flashlight' analogy is used to help visualize the process of finding the area between two polar curves. It likens the process to shining a flashlight along the cave walls (the polar curves) to illuminate the space (the area) between them, which helps students understand how to set up the integral for calculating the area.
How does the speaker handle the transition from rectangular to polar coordinates in the video?
-The speaker emphasizes the importance of understanding the transition between rectangular and polar coordinates, especially when x and y values appear in polar problems. He provides a formula to convert these values into polar coordinates (x = r*cos(θ), y = r*sin(θ)), and stresses the importance of using these formulas to bridge the gap between the two coordinate systems.
What is the main takeaway from the video regarding the AP exam and polar coordinates?
-The main takeaway is that while polar coordinates can be challenging, with practice and the right strategies, students can master the concepts and tackle the common problem types they might encounter on the AP exam. The speaker provides tips, strategies, and additional practice problems to help students prepare.
How does the speaker use technology to aid in the explanation of polar coordinates?
-The speaker uses graphing calculators and software like the TI-Inspire to visualize and solve problems related to polar coordinates. He demonstrates how to graph polar equations, find intersection points, and evaluate functions at specific angles, which helps students understand the concepts more concretely.
What is the significance of the speaker's mention of trigonometric identities in relation to the AP exam?
-The speaker clarifies that while trigonometric identities are important in high school mathematics, they are not required for the AP exam when dealing with polar coordinates. The focus is on understanding the calculus concepts and being able to interpret and explain the results, rather than memorizing and applying identity formulas.
Outlines
📚 Introduction to Polar Coordinates Review
The video begins with the host welcoming viewers back to the seventh day of the AP Calculus BC live review for 2022. The focus for the day is on polar coordinates, with the host expressing excitement about the topic and revealing a new tattoo related to polar coordinates. The host, Tony Record, introduces his co-host, Brian Passwater, and they discuss the common struggles students face with polar coordinates on the AP exam. They emphasize the importance of practice and strategy in tackling these problems and provide an overview of what will be covered in the video, including area calculations between polar curves, conversion formulas, and understanding the slope of tangent lines in polar coordinates.
📊 Understanding Polar Graphs and Area Calculation
This paragraph delves into the specifics of calculating areas between polar curves. The host explains that the approach for area calculation in polar coordinates is different from rectangular coordinates, using a 'sweeping' method rather than creating rectangles. The formula for calculating polar area is emphasized, with the importance of including the 1/2 constant and squaring the r value. The host also discusses the common mistakes made by students when finding the limits of integration and the significance of understanding the natural habitat of x and y in polar problems. The video provides a step-by-step guide on how to set up and solve such problems using a calculator, highlighting the need for accuracy in the answers.
🌐 Trigon Identities and Polar Coordinates
The host clarifies that while certain trigonometric identities are taught in high school, they are not required for the AP exam. The focus is on understanding the calculus aspect of polar coordinates. The video moves on to discuss the importance of understanding the conversion formulas between polar and rectangular coordinates, especially when x or y appears in a polar problem. The concept of r representing the distance from the origin in polar graphs is also explained, emphasizing that r can be negative and its absolute value should be considered. The host also mentions the increasing trend of interpretation or explanation questions in the AP exam, requiring a deeper understanding of concepts rather than just formula memorization.
📈 Practice Problems and Calculator Usage
The video continues with a series of practice problems related to polar coordinates. The host demonstrates how to use a calculator to find the area of a region bounded by a polar curve, emphasizing the importance of setting up the problem correctly. The video also addresses the common mistakes made by students when solving these problems, such as forgetting the 1/2 constant, not squaring the r value, and struggling to find the correct limits of integration. The host provides detailed instructions on how to use the calculator effectively, including how to input the correct functions and interpret the results.
🤔 Interpreting Polar Coordinates and Graphs
The host discusses the importance of interpreting polar coordinates and graphs, especially in the context of the AP exam. The video provides a detailed explanation of how to find the values of r and the y-coordinate of a polar curve at a given theta value, and how to explain these values in terms of the graph. The host uses a graphing calculator to find the intersection point of two polar curves and explains how to set up the calculator to solve the problem. The video also touches on the concept of the extreme value theorem and how it applies to finding maximum distances in polar coordinates.
🏆 Final Tips and Tattoo Reveal
In the final part of the video, the host provides a summary of the key points covered in the review of polar coordinates. The host emphasizes the importance of practice and offers tips for tackling multiple-choice and free-response questions on the AP exam. The video concludes with the host sharing a personal anecdote about getting a matching tattoo with his wife related to polar coordinates, symbolizing their shared love for mathematics. The host encourages viewers to download additional practice materials and looks forward to the final tips and strategies for the AP exam in the next session.
Mindmap
Keywords
💡Polar Coordinates
💡Tangent Line
💡Area Calculation
💡Conversion Formulas
💡Polar Graphs
💡AP Exam
💡Graphing Calculator
💡Polar Curves
💡Derivative
💡Integration
Highlights
The video is part of a live review series for 2022 Calculus BC, focusing on polar coordinates.
The speaker plans to reveal a new tattoo related to polar coordinates at the end of the video.
Polar coordinates are a common area of struggle for students on the AP exam.
The video provides tips and strategies for tackling common polar coordinate problem types.
The presenter emphasizes the importance of practice in mastering polar coordinate concepts.
The video discusses finding the area between one or two polar curves using the area formula.
Conversion formulas between polar and rectangular coordinates are crucial for solving certain problems.
The slope of a tangent line in polar coordinates is derived as dy/dx = (dy/dθ) / (dx/dθ).
Understanding the concept of r in polar coordinates, including its potential negativity, is important.
The video addresses the increasing presence of interpretation and explanation questions in recent AP exams.
Trigonometric identities are not required for the AP exam, despite their presence in high school curricula.
The video includes a detailed walkthrough of calculating the area of a polar region using integration.
Calculator use is encouraged for efficiency and accuracy in solving polar coordinate problems.
The presenter shares a personal story of getting a matching tattoo with his wife related to mathematical concepts.
The video concludes with a reminder to download supplementary materials for additional practice.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: