AP Calculus BC Lesson 9.3
TLDRThis video lesson delves into the concept of arc length for parametric equations, emphasizing the integral formula for calculating it. The script walks through several examples, demonstrating how to set up and solve integrals for the arc length of curves defined by parametric equations over given time intervals. It also touches on using calculators for these calculations and hints at future topics like velocity vectors.
Takeaways
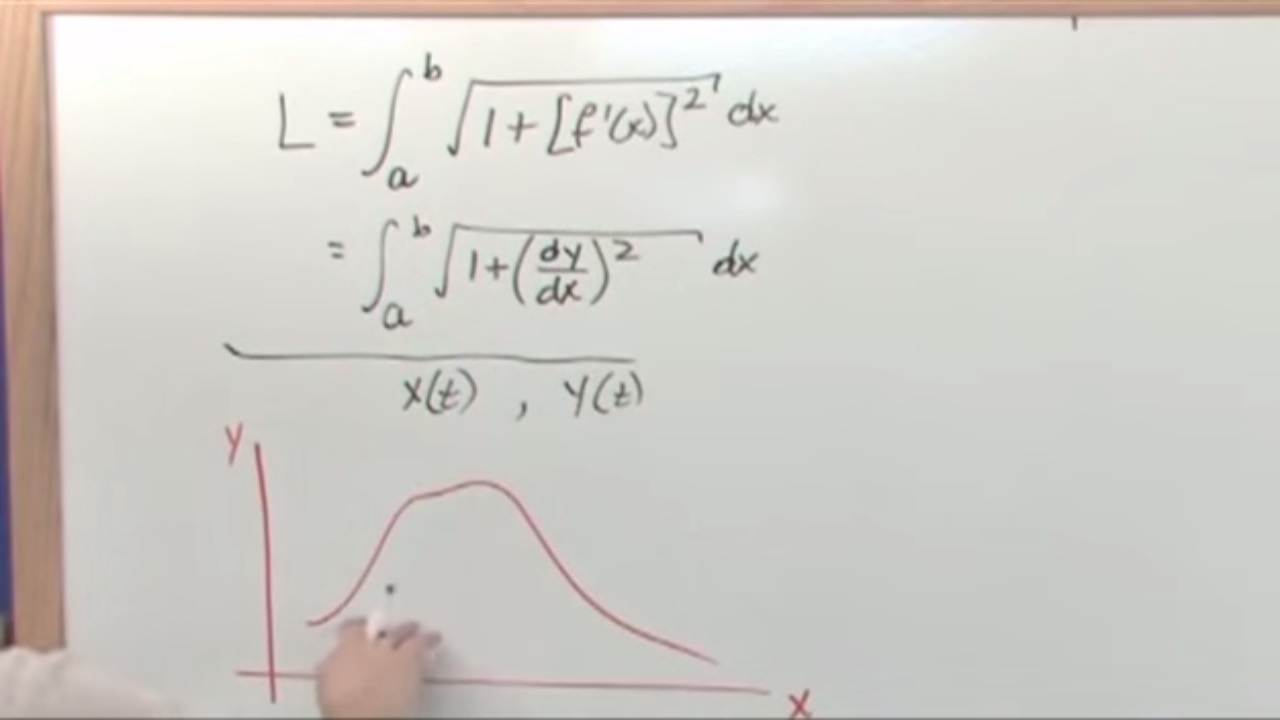
- π The arc length formula for parametric equations is discussed, which is similar to the one from lesson 8.13: L = β«(β(1 + (dx/dt)^2 + (dy/dt)^2)) dt from time A to time B.
- π The script provides an example of finding the arc length of a curve defined by parametric equations x(t) = 5t^3 - t and y(t) = t^2/3 from t = 0 to t = 2, resulting in an arc length of 38.382.
- π The process of setting up and solving the integral for the arc length is demonstrated, including finding the derivatives with respect to the parameter t.
- π Another example is given for a curve defined by x(t) = 5t and y(t) = 2t^3 from t = 0 to t = 4, which matches answer choice A when set up correctly.
- π The script explains how to find the arc length of a path described by x(t) = 2cos(t) and y(t) = 3sin(t) from Ο/2 to Ο, with the correct answer being choice C.
- π The length of a curve traced by x(t) = 4e^t and y(t) = 5.4cos(e^t) from t = 0 to t = 2 is calculated to be 34.875.
- π A calculator-free response question is discussed, involving a particle moving along a curve with given dx/dt and dy/dt, from time T = 4 to T = 6, resulting in a distance of 12.136.
- π The concept of velocity vectors is introduced, which will be formally discussed in a future video.
- π€οΈ The total distance traveled by a particle is synonymous with arc length when dealing with parametric equations.
- π The script concludes with an example of finding the total distance traveled by a particle from time T = 0 to T = 1, with the answer being 4.073.
- π The script emphasizes the importance of setting up the integral correctly and using the arc length formula to find the length of curves defined by parametric equations.
Q & A
What is the arc length formula for parametric equations?
-The arc length formula for parametric equations is given by L = β« from A to B of the square root of (DX/DT)^2 + (DY/DT)^2, where A and B represent different times for the parametric functions.
How is the arc length formula derived?
-The arc length formula for parametric equations is derived from the general arc length formula for functions, which is similar in form. However, the exact derivation is not covered in the video transcript provided.
What are the parametric equations for the curve whose length is to be found in the first example?
-The parametric equations for the curve in the first example are X(T) = 5T^3 - T and Y(T) = T^2/3, from T = 0 to T = 2.
What is the integral set up to calculate the arc length of the curve in the first example?
-The integral set up to calculate the arc length is β« from 0 to 2 of the square root of (15T^2 - 1)^2/T^2 + (2/3T)^2 with respect to T.
What is the numerical result for the arc length of the curve in the first example?
-The numerical result for the arc length of the curve in the first example is approximately 38.382 units.
What are the parametric equations for the curve in the second example?
-The parametric equations for the curve in the second example are X(T) = 5T and Y(T) = 2T^3, from T = 0 to T = 4.
How do you find the derivatives for the arc length integral in the second example?
-The derivatives for the arc length integral in the second example are found by differentiating the parametric equations with respect to T, resulting in DX/DT = 5 and DY/DT = 6T^2.
What is the integral set up to calculate the arc length of the curve in the second example?
-The integral set up to calculate the arc length is β« from 0 to 4 of the square root of 5^2 + (6T^2)^2 with respect to T.
What are the parametric equations for the curve in the third example?
-The parametric equations for the curve in the third example are X(T) = 4e^T and Y(T) = 5.4cos(e^T), from T = 0 to T = 2.
What is the numerical result for the arc length of the curve in the third example?
-The numerical result for the arc length of the curve in the third example is approximately 34.875 units.
How do you calculate the total distance traveled by a particle along a curve?
-The total distance traveled by a particle along a curve is calculated using the arc length formula for parametric equations, where the functions represent the particle's position with respect to time.
What is the velocity vector given for the particle in the last example?
-The velocity vector given for the particle in the last example is V(T) = sin(e^0.36T), 7.8T, representing the rates of change of the x and y positions with respect to time T.
Outlines
π Calculating Arc Length of Parametric Equations
This paragraph introduces the concept of arc length for parametric equations, referencing the arc length formula from a previous lesson. It explains that the formula for parametric equations is similar to the one for functions, with the integral running from time A to time B. An example is provided where the arc length is calculated for a specific set of parametric equations from time 0 to 2. The process involves setting up the integral and using a calculator to find the numerical answer, which is given as 38.382.
π Arc Length Formula Application for Different Parametric Equations
The paragraph continues with the application of the arc length formula for parametric equations. It provides two additional examples: one involving the parametric equations X of T equals 5T and Y of T equals 2T cubed from T equals 0 to T equals 4, and another involving X equals 2 times the cosine of T and Y equals 3 times the sine of T from T equals Ο/2 to T equals Ο. For each, the paragraph outlines the steps to find the derivatives and set up the integral to calculate the arc length, matching the results with given answer choices.
π Length of a Curve Traced by Parametric Equations
This section discusses the calculation of the length of a curve traced by parametric equations X of T equals 4e to the power of T and Y of T equals 5.4 times the cosine of e to the power of T from T equals 0 to T equals 2. The integral is set up for this interval, and the derivatives are calculated to find the arc length, which is given as 34.875. The paragraph also includes a calculator-free response question related to the topic, where the arc length formula is used to find the distance a particle travels along a curve from time T equals 4 to T equals 6.
π Total Distance Traveled by a Moving Particle
The final paragraph addresses the calculation of the total distance traveled by a particle moving along a curve in the XY plane. Given the position X of t y of t and the velocity vector V of T, the paragraph explains how to use the arc length formula to find the distance from time T equals 0 to T equals 1. The integral is set up using the velocity components as derivatives, and the calculation yields a distance of 4.073. The paragraph emphasizes that the units are not specified, so the answer is presented as a numerical value.
Mindmap
Keywords
π‘arc length
π‘parametric equations
π‘integral
π‘derivative
π‘square root
π‘time
π‘calculus
π‘graphing calculator
π‘chain rule
π‘natural log
π‘velocity vector
Highlights
Discussion of arc length for parametric equations.
Recall of the arc length formula from a previous lesson.
Explanation of the integral formula for calculating arc length.
Use of different variables (A and B) to represent starting and ending x values in the arc length formula.
Transition to the arc length formula for parametric equations involving different times (A and B).
Example calculation of the arc length of a curve defined by specific parametric equations.
Integration of the square root of the sum of derivatives squared over a time interval.
Demonstration of how to set up a problem for calculator integration.
Mention of using calculator's parametric mode for solving problems.
Another example involving finding the arc length of a curve defined by different parametric equations.
Explanation of the process to find the arc length of a path described by parametric equations involving trigonometric functions.
Calculation of the arc length of a curve traced by exponential and trigonometric functions.
Illustration of how to set up and solve a calculator-free response question involving arc length.
Description of a particle's movement along a curve and the calculation of its total distance traveled.
Use of the arc length formula to find the distance a particle travels between two time points.
Inference of velocity vector components from given parametric equations.
Calculation of the total distance traveled by a particle using its velocity vector components.
Final answer provided for the distance traveled by a particle over a given time interval.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: