Simple Harmonic Motion - Physics 101 / AP Physics 1 Review with Dianna Cowern

Physics Girl

15 Jan 202126:56

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Dianna Cowern explores simple harmonic motion, using a pendulum to demonstrate the concept. She explains how the period of a pendulum's swing is dependent on the length of the string and gravity, not the mass of the object. Through experiments and mathematical derivations, she shows the relationship between pendulum motion and spring oscillation, revealing the formula for the period of a pendulum and its practical applications, such as estimating the height of a tree branch or understanding the workings of a grandfather clock.

Takeaways

🏓 Simple Harmonic Motion (SHM) refers to systems that oscillate back and forth with a restoring force proportional to the displacement.
🎯 The period of oscillation for SHM systems is constant and is independent of the mass of the object involved.
🌳 The conservation of energy principle is fundamental in understanding SHM, as potential energy is converted to kinetic and back during oscillation.
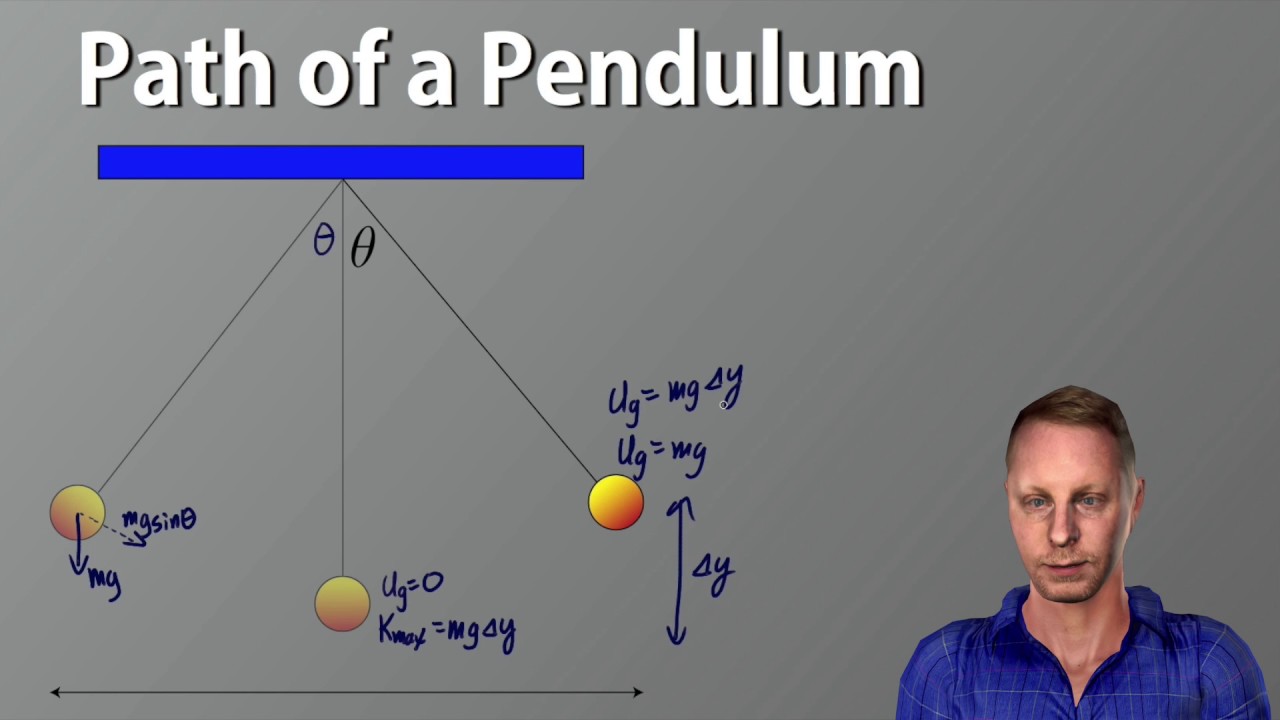
⏱ The period of a pendulum is solely dependent on the length of the string (L) and the acceleration due to gravity (g), not the mass of the pendulum.
📚 Galileo's observations in the 16th century laid the groundwork for understanding that the period of a pendulum is independent of the mass of the object.
📐 Small angle approximation allows us to approximate the sine of an angle as the angle itself in radians, simplifying the equations for SHM.
🔗 The restoring force in a pendulum can be modeled as being directly proportional to the displacement from the equilibrium position, similar to a spring.
📉 The acceleration of an object in SHM is directly related to its displacement, with no dependency on the object's mass once it's in motion.
📚 The mathematical models for both pendulums and springs are similar, especially when considering small angular displacements.
📏 The period of a pendulum can be calculated using the formula \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( T \) is the period, \( L \) is the length of the string, and \( g \) is the acceleration due to gravity.
🛠 The principles of SHM are applied in various real-world scenarios, including the operation of grandfather clocks and the design of car suspension systems.

Q & A

What is the main concept discussed in the video script?
-The main concept discussed in the video script is simple harmonic motion, which involves systems that oscillate back and forth, such as a pendulum or a spring.
What is the significance of the bowling ball demonstration in the video?
-The bowling ball demonstration is used to illustrate the conservation of energy and to introduce the concept of simple harmonic motion, showing how the ball swings back and forth without smashing the presenter's face.
What is the period of oscillation and how is it measured in the video?
-The period of oscillation, or simply the period, is the time it takes for one full return trip of an oscillating object. In the video, the period is measured using video editing software to time the bowling ball's swing, which took 4.125 seconds.
Why does the mass of the pendulum's bob not affect the period of a pendulum?
-The mass of the pendulum's bob does not affect the period because, in the case of simple harmonic motion with small angles, the restoring force is proportional to the displacement (x) and the masses cancel out when applying Newton's second law, leaving only the length of the string and the acceleration due to gravity as factors.
How does the length of the string affect the period of a pendulum?
-The length of the string affects the period of a pendulum because the period is directly proportional to the square root of the length of the string (L), as shown in the formula T = 2π√(L/g), where g is the acceleration due to gravity.
What is the small angle approximation, and why is it used in the video?
-The small angle approximation is a simplification used when the angle of displacement (theta) is small enough that the sine of the angle can be approximated as equal to the angle itself (sin(θ) ≈ θ). It is used in the video to simplify the calculations and to show that the restoring force is directly proportional to the displacement for small angles.
How is the relationship between a pendulum and a spring demonstrated in the video?
-The video demonstrates that both a pendulum and a spring involve a linear restoring force proportional to displacement, which is a key characteristic of simple harmonic motion. The mathematical models for both systems look similar, especially when the pendulum is at small angles.
What is the significance of the cosine function in describing the position of a pendulum?
-The cosine function is used to describe the position of a pendulum because it is a sinusoidal function that represents the oscillation of the pendulum. At time equals zero, the cosine function is at its maximum, which corresponds to the maximum displacement of the pendulum at the start of its swing.
How does the video script relate the acceleration of a pendulum to its period?
-The script uses calculus to show that the acceleration of a pendulum is the second derivative of its position and is proportional to the displacement, which leads to the formula for the period of a pendulum: T = 2π√(L/g).
What is the practical application of understanding the period of a pendulum, as shown in the video?
-Understanding the period of a pendulum allows one to calculate the length of the pendulum or the height of a point above the pendulum's rest position, as demonstrated when the presenter calculates the height of a tree branch using the measured period of the pendulum's swing.
How does the video script explain the historical connection between the pendulum and the definition of the meter?
-The script explains that during the French Revolution, the French Academy of Sciences considered defining the standard meter based on a pendulum that swings one second per cycle. This idea was inspired by the fact that a simple pendulum with a length of one meter has a period close to two seconds.

Outlines

00:00

🎱 Introduction to Simple Harmonic Motion

In this introductory paragraph, Dianna Cowern sets the stage for a lesson on simple harmonic motion (SHM), a topic that involves objects moving back and forth in a periodic manner. She begins with a personal anecdote about tying a bowling ball to a tree to demonstrate the conservation of energy without injury. The main goal of the lesson is to determine the height of the tree branch by observing the time it takes for the bowling ball to swing. The paragraph introduces the concept of SHM, provides examples of what does and does not constitute SHM, and emphasizes the importance of understanding the principles behind SHM. It also touches on the conservation of energy as a tool for modeling SHM.

05:01

🔍 Exploring the Physics of Simple Harmonic Motion

This paragraph delves into the physics behind simple harmonic motion, focusing on the conservation of energy and the role of gravitational potential energy and kinetic energy in the swinging of a bowling ball. The concept of the period of oscillation is introduced, with the period being the time it takes for one full swing and return. The paragraph also discusses the factors that affect the period of a pendulum, revealing that only the length of the string and the acceleration due to gravity are significant, while the mass of the object does not. The historical discovery by Galileo that the period of a pendulum is independent of its mass is highlighted, and the Foucault pendulum is mentioned as an example of a pendulum with a changing period due to Earth's rotation.

10:04

📚 Mathematical Modeling of Simple Harmonic Motion

The speaker transitions to the mathematical modeling of simple harmonic motion, starting with the force experienced by a pendulum and using the small angle approximation to simplify the calculations. The relationship between the restoring force, displacement, and the physical properties of the pendulum is established. By applying Newton's second law, the paragraph shows that the acceleration of the pendulum is independent of its mass, which is a key insight into the nature of SHM. The connection between the pendulum and a spring is made, highlighting the linear restoring force in both systems and setting the stage for further mathematical exploration.

15:04

📐 Calculus and the Period of a Pendulum

This paragraph introduces the use of calculus to relate the acceleration of the pendulum to its period. The acceleration is described as the second derivative of position, and the properties of sine and cosine functions are used to model the pendulum's motion. The angular frequency, ω, is introduced as a key variable, and the relationship between ω and the period of the pendulum is established. The formula for the period of a pendulum, T = 2π√(L/g), is derived, where L is the length of the string and g is the acceleration due to gravity. This formula is central to understanding the period of a pendulum and its dependence solely on the length of the string and the local gravity.

20:06

🌳 Practical Application: Determining the Height of a Tree Branch

The speaker applies the theoretical knowledge from the previous paragraphs to a practical problem: determining the height of a tree branch by using the period of a pendulum. The process involves using the measured period of the pendulum's swing and the known gravitational acceleration to calculate the length of the string, which is then used to estimate the height of the branch. The historical context of the meter's definition and its relation to the pendulum's period is also discussed, highlighting the close relationship between the period of a one-meter pendulum and one second.

25:07

🛠 Further Exploration of Simple Harmonic Motion

The final paragraph expands on the concept of simple harmonic motion, discussing its various applications and manifestations in everyday life and physics. Examples such as vibrating guitar strings, bouncing balls, and rolling marbles are used to illustrate SHM. The distinction between simple harmonic motion and more complex oscillations is made clear, emphasizing the importance of the linear restoring force. The period of a spring's oscillation is also introduced, with a formula provided that relates it to the mass and spring constant. The paragraph concludes with a guest message from Kyle, a member of the United States Space Force, who emphasizes the practical applications of physics in his field and encourages viewers to pursue their interest in the subject.

Mindmap

Keywords

💡Simple Harmonic Motion

Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force on an object is directly proportional to the displacement from its rest position and is always directed towards that position. In the context of the video, SHM is the central theme, as it discusses the back-and-forth motion of objects like a pendulum or a spring. The video uses the example of a bowling ball swinging to demonstrate SHM and to explain the underlying physics.

💡Conservation of Energy

Conservation of Energy is a fundamental principle stating that the total energy in an isolated system remains constant over time. In the video, this principle is used to explain the behavior of the bowling ball as it swings, transitioning between kinetic energy (when it's moving) and gravitational potential energy (when it's at the peak of its swing). The script illustrates this with the bowling ball's motion, showing how energy is conserved throughout its swing.

💡Period of Oscillation

The period of oscillation, or simply 'period,' is the time taken for one complete cycle of motion. The video emphasizes the importance of the period in SHM, noting that it remains constant for a given system. The script measures the period of the bowling ball's swing to be 4.125 seconds, which is crucial for determining the height of the tree branch in the demonstration.

💡Foucault Pendulum

A Foucault Pendulum is a large pendulum that demonstrates the Earth's rotation by the path it traces over time. The video script introduces the Foucault Pendulum to contrast it with a simple pendulum, showing that while both exhibit oscillation, a Foucault Pendulum's path changes due to the Earth's rotation, unlike the consistent motion of a simple pendulum in SHM.

💡Restoring Force

Restoring force is the force that brings an object back to its equilibrium or rest position when it is displaced. In the context of SHM, the video explains how the restoring force for a pendulum is the component of gravitational force acting along the direction of the string, which is proportional to the displacement (x) and is given by mg sin(theta), where m is mass, g is gravitational acceleration, and theta is the angle of displacement.

💡Small Angle Approximation

The small angle approximation is a simplification used in trigonometry where the sine of a small angle (typically less than 15 degrees) is approximated as equal to the angle itself in radians. The video uses this approximation to simplify the calculation of the restoring force, stating that for small angles, mg sin(theta) can be approximated as mg theta, making the force linearly proportional to displacement.

💡Newton's Second Law

Newton's Second Law of Motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma). In the video, this law is applied to derive the equation for the acceleration of the pendulum, showing that the mass cancels out, indicating that the period of oscillation is independent of the mass of the object.

💡Angular Frequency

Angular frequency, denoted by omega (ω), is a measure of how fast an object undergoes SHM, expressed in radians per second. The video relates angular frequency to the period of the pendulum, using it to derive the formula for the period of a simple pendulum in SHM, which is T = 2π√(L/g), where L is the length of the string and g is the acceleration due to gravity.

💡Derivative

In calculus, a derivative is a measure of how a function changes as its input changes. The video explains that acceleration is the second derivative of position with respect to time, which is key to describing SHM. The script uses the concept of derivatives to relate the position, velocity, and acceleration of the pendulum in its motion.

💡Sinusoidal Functions

Sinusoidal functions, such as sine and cosine, are mathematical functions that describe smooth, periodic oscillations. The video script describes how the position of a pendulum in SHM can be modeled using the cosine function, while its velocity is represented by a sine function, illustrating the phase difference between position and velocity in SHM.

💡Spring Constant

The spring constant, denoted by k, is a measure of the stiffness of a spring. It appears in Hooke's Law, which states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position (F = -kx). The video uses the spring constant in the context of a car's suspension system, providing an example of how to estimate it based on the car's oscillation frequency and mass.

Highlights

Dianna Cowern demonstrates the conservation of energy using a bowling ball tied to a tree at Simone's workshop.

The lesson explores how to determine the height of a tree branch by observing the swing of a bowling ball.

Introduction to simple harmonic motion (SHM) and its characteristics with examples like a swinging bowling ball and a vibrating spring.

Explanation of why certain activities, like a ball in ping-pong, are not considered SHM due to their complex motion.

Use of conservation of energy to model SHM, illustrating the conversion between gravitational potential and kinetic energy.

Measurement of the bowling ball's period of oscillation, revealing its consistency and significance in SHM.

Discussion on the factors affecting the period of a pendulum, highlighting that only the string's length and gravity's acceleration matter.

Historical note on Galileo's observations of pendulum motion in church, leading to the understanding that mass does not affect the period.

Derivation of the relationship between a pendulum and a spring using the small angle approximation for restoring force.

Explanation of how the restoring force in SHM is linear and proportional to displacement, similar to a spring.

Application of Newton's second law to show that the pendulum's acceleration is independent of mass.

Introduction to calculus and its role in understanding the relationship between acceleration, velocity, and position in SHM.

Identification of sine and cosine functions as the basis for describing the motion of SHM due to their derivatives.

Calculation of the pendulum's period using the formula T = 2π√(L/g), emphasizing the dependence on string length and gravity.

Practical application of SHM principles to estimate the height of a tree branch based on the period of a pendulum's swing.

Historical context on the French Revolution's influence on the definition of the meter in relation to a pendulum's period.

Explanation of how the principles of SHM are applied in various real-world scenarios, including car suspension and grandfather clocks.

Final problem demonstrating the estimation of a car's spring constant based on its oscillation frequency and mass.

Emphasis on the simplified nature of the SHM model and its practical applications despite its limitations at larger angles.

Encouragement from Kyle, a member of the United States Space Force, highlighting the importance of physics in various space-related applications.

Transcripts

Browse More Related Video

Simple Harmonic Motion

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

Pendulums | Oscillations and mechanical waves | Physics | Khan Academy

AP Physics 1 - Pendulums

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy

AP Physics Workbook 6.G Period and Amplitude for SHM

Related Tags

Physics Education Harmonic Motion Bowling Ball Pendulum Swing Conservation Laws Energy Conversion Galileo's Discovery Spring Analogy Calculus Application Clock Mechanics