Video 76 - Curvature Basics
TLDRThis video, the 76th in the tensor calculus series, delves into the geometric nature of a line's curvature in space. It builds on the concept of the first derivative of the position vector with respect to arc length, which yields the unit tangent vector. The focus then shifts to the implications of the second derivative, exploring its role as a measure of the rate of change in the direction of the unit vector. The video introduces the principal normal and curvature, represented by the Greek letter kappa, and explains their significance in describing how a curve bends. It concludes with a geometric demonstration of curvature for a circle, revealing the relationship between curvature and the radius of curvature, and ends with a visual demonstration of these concepts on a spiral, emphasizing the changing curvature and radius of curvature as one moves along the curve.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on the geometric nature of the curvature of a line in space.
- 🔍 The first derivative of the position vector with respect to arc length yields a unit vector tangent to the curve at the point of evaluation.
- 🔄 The second derivative of the position vector with respect to arc length is explored, representing the rate of change of the direction of the unit tangent vector.
- 🧭 The unit tangent vector's change in direction is the only variable as its length remains constant at one, making the second derivative a measure of directional change rate.
- ⚖️ The derivative of the unit vector is orthogonal to the unit vector itself, indicating a right angle between the rate of change vector and the tangent.
- 📉 The curvature, represented by the Greek letter kappa, is introduced as a scalar value measuring the magnitude of the rate of change of direction.
- 📍 The principal normal, a unit vector perpendicular to the tangent vector, points in the direction of the rate of change of the tangent vector.
- 🌀 For a circle, the curvature is constant and equal to the reciprocal of the circle's radius, introducing the concept of the radius of curvature.
- 📈 The principal normal is undefined in straight sections of a curve and is piecewise continuous, only defined where the curve bends.
- 🛠 The principal normal and tangent vector together define the plane of curvature, which can vary in three-dimensional space.
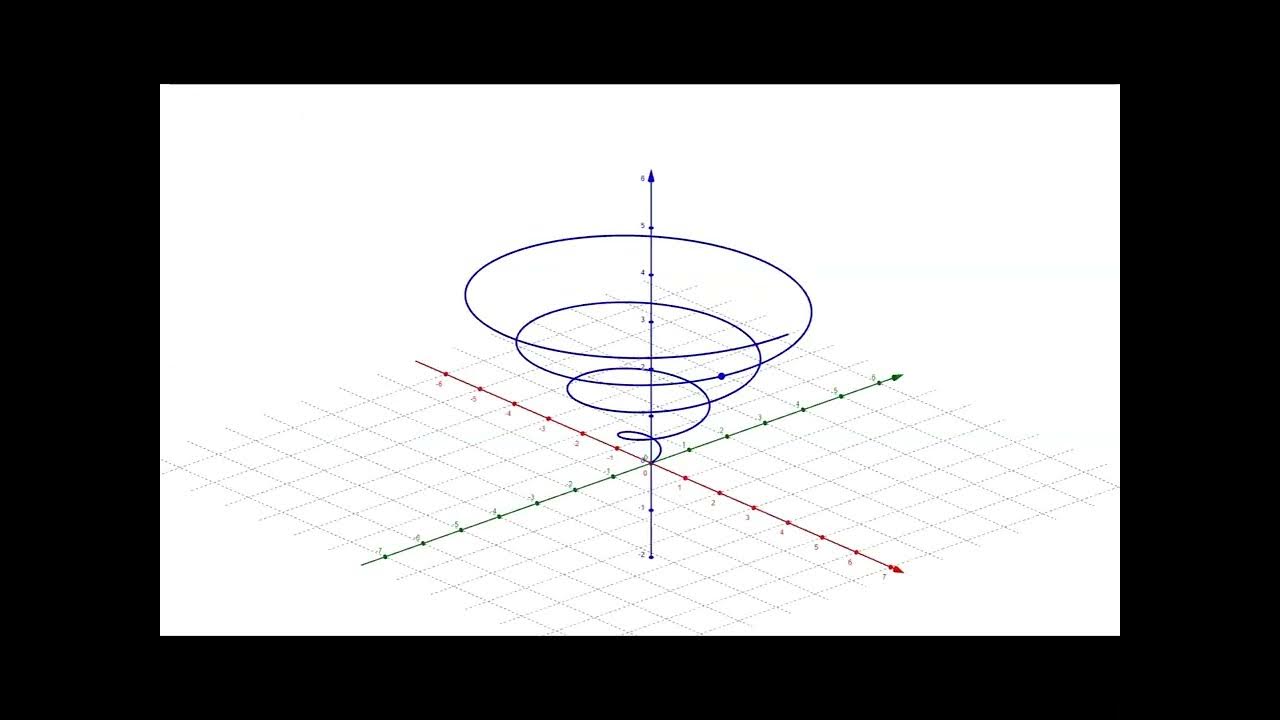
- 🎥 A visual demonstration using a spiral illustrates the concepts of curvature, principal normal, and the changing radius of curvature along the curve.
Q & A
What is the main topic of this video in the tensor calculus series?
-The main topic of this video is the exploration of the geometric nature of the curvature of a line in space, specifically focusing on the meaning of taking the second derivative of the position vector with respect to arc length.
What is the significance of the first derivative of the position vector with respect to arc length?
-The first derivative of the position vector with respect to arc length gives a unit vector, denoted as s-hat, which is always tangent to the curve at the point of evaluation.
What does the second derivative of the position vector with respect to arc length represent?
-The second derivative of the position vector with respect to arc length represents the rate of change of the unit tangent vector's direction as it moves along the curve, which is a measure of the curvature.
Why is the derivative of the unit vector s-hat with respect to arc length orthogonal to the unit vector itself?
-The derivative of the unit vector s-hat with respect to arc length is orthogonal to the unit vector itself because the unit vector is of constant length and only its direction can change, making the rate of change of direction perpendicular to the direction itself.
What is the principal normal and how is it related to the curvature of a curve?
-The principal normal is a unit vector, denoted as p-hat, that points in the direction of the rate of change of the unit tangent vector's direction. It is perpendicular to the tangent vector and is used to define the plane of curvature.
What is the curvature represented by the Greek letter kappa (κ)?
-The curvature, represented by kappa (κ), is a scalar value that quantifies the magnitude of the rate of change of the direction of the unit tangent vector, indicating how sharply the curve is turning.
Why is the principal normal undefined in a straight section of a curve?
-The principal normal is undefined in a straight section of a curve because there is no curvature, and thus no direction of turning to define the normal's orientation.
How is the curvature of a circle related to its radius?
-For a circle, the curvature (kappa) is equal to the reciprocal of its radius. This means that the larger the radius, the smaller the curvature, indicating a less sharp turn.
What is the radius of curvature and how does it relate to the curvature of a curve?
-The radius of curvature is an alternative way to express the curvature of a curve, where it is the radius of the circle that has the same curvature as the curve at a particular point. It is the reciprocal of the curvature value.
How does the video script demonstrate the concepts of curvature and principal normal without using a coordinate system?
-The video script demonstrates the concepts of curvature and principal normal using geometric objects and relationships, such as the unit tangent vector, the rate of change of direction, and the principal normal's orientation, without referencing a specific coordinate system.
What is the purpose of the visual demonstration with the spiral in the video?
-The visual demonstration with the spiral serves to provide a clear visualization of the concepts introduced, showing how the position vector, unit tangent vector, principal normal, and curvature change as the curve is traced.
Outlines
📐 Introduction to Curvature of a Line in Space
This paragraph introduces the concept of curvature of a line in space, building upon the understanding of the first derivative of a position vector with respect to arc length, which results in a unit tangent vector. The focus shifts to exploring the implications of the second derivative, which is the rate of change of the unit vector's direction along the curve. The unit tangent vector's constancy in length implies that any change must be in direction, indicating a measure of how quickly the direction changes as the vector moves along the curve.
🔍 Deriving the Curvature and Principal Normal
The second paragraph delves into the mathematical representation of curvature, starting with the derivative of the unit tangent vector with respect to arc length. It uses the dot product and the product rule to establish that the derivative of the unit tangent vector is orthogonal to the vector itself. This leads to the definition of curvature as a scalar value, represented by kappa (κ), and the principal normal, a unit vector denoted by p̂ that points in the direction of this derivative. The principal normal is undefined in straight sections of the curve and varies in direction as the curve bends in space.
🌀 Special Case: Curvature of a Circle
This paragraph examines the curvature of a circle as a special case, leveraging the circle's symmetry to argue that the rate of change of the unit tangent vector's direction is constant. The curvature is determined geometrically by comparing the change in the tangent vector to the arc length over which it changes. The result is that the curvature of a circle is the reciprocal of its radius, introducing the concept of the radius of curvature as an alternative way to express curvature, with the two parameters being reciprocals of each other.
🌐 Visualizing Curvature with a Spiral
The final paragraph provides a visual demonstration of the curvature concepts using a spiral. It discusses the unit tangent vector and the principal normal, showing how they move in tandem around the curve and are orthogonal to each other. The principal normal points toward the axis of the spiral, indicating the direction of curvature. The paragraph also illustrates how the curvature and radius of curvature change along the spiral, with the curvature decreasing and the radius of curvature increasing as the spiral widens. The visual aids in understanding how the curvature is defined by the plane containing the tangent vector and the principal normal.
Mindmap
Keywords
💡Tensor Calculus
💡Curvature
💡Arc Length
💡Unit Tangent Vector
💡Second Derivative
💡Dot Product
💡Orthogonal
💡Principal Normal
💡Kappa (Curvature Scalar)
💡Radius of Curvature
💡Geometric Objects
Highlights
Exploration of the geometric nature of the curvature of a line in space.
Introduction of the relationship between the first derivative of the position vector and the unit tangent vector.
Investigation of the second derivative of the position vector with respect to arc length as a measure of the rate of change of direction.
Explanation that the unit vector s-hat is always tangent to the curve at the point of evaluation.
Derivation of the orthogonality between the derivative of the unit vector and the unit vector itself.
Visual representation of the unit vector's direction change along the curve.
Introduction of the concept of curvature represented by the Greek letter kappa.
Definition of the principal normal as a unit vector pointing in the direction of the rate of change of the unit tangent vector.
Discussion on the piecewise continuity of the principal normal in areas where the line is curving.
Illustration of the principal normal pointing in various directions depending on the curvature in space.
Explanation of how the principal normal and tangent vector define the plane of curvature.
Special case analysis of a circle's curvature and its constant rate of direction change.
Geometric determination of curvature for a circle by comparing vector change to arc length change.
Demonstration that the curvature of a circle is the reciprocal of its radius.
Introduction of the radius of curvature as an alternative way to express curvature.
Visual demonstration of a spiral curve with changing curvature and radius of curvature.
Explanation of how the curvature and radius of curvature values change along the spiral curve.
Visualization of the plane defined by the tangent vector and principal normal vector.
Emphasis on the geometric approach used throughout the video without reference to a coordinate system.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: