Video 11 - Vector Transformations
TLDRThis video from a tensor calculus series delves into transforming vectors between coordinate systems, introducing the concept of covariant basis vectors. It explains the Jacobian, a matrix of partial derivatives, as a key to understanding covariant and contravariant transformations. The video clarifies that covariant objects, represented with lower indexes, transform in the same way as the basis vectors, while contravariant objects, with upper indexes, follow a different rule. The script aims to demystify tensor calculus by illustrating how these transformations apply to vectors and other derivative objects, emphasizing the importance of index positions in determining transformation types.
Takeaways
- 📚 The video focuses on transforming vectors between coordinate systems, building on earlier videos that discussed transforming coordinate values.
- 🧭 The basis vectors discussed in previous videos are identified as covariant basis vectors, and this video explains why they are called 'covariant'.
- 🔄 The video introduces a process using a composite function to understand how vectors transform between coordinate systems.
- 📐 The covariant basis vectors are defined in both the original coordinate system and the alternate (z prime) system.
- 🧩 The Jacobian matrix, which represents the partial derivatives of one coordinate system with respect to another, plays a crucial role in transforming vectors between these systems.
- 🔢 A covariant transformation is defined as a transformation where the free index is in the lower position, and objects that transform this way are covariant in nature.
- 📈 Contravariant transformations are introduced, where the free index is in the upper position, and objects transforming this way are contravariant in nature.
- ⚖️ The video emphasizes the importance of understanding the relationship between the covariant and contravariant transformations.
- 🔀 The video discusses how the combination of covariant basis vectors and contravariant scalar components results in an invariant object.
- 🧠 The terms 'covariant' and 'contravariant' describe how objects vary with respect to coordinate transformations, which is essential for understanding tensor calculus.
Q & A
What is the main focus of this video on tensor calculus?
-The main focus of this video is to teach how to transform vectors from one coordinate system to another and to explain why the basis vectors discussed in previous videos are called covariant basis vectors.
What is a covariant basis and how is it defined?
-A covariant basis is a set of vectors that are used to express other vectors in a coordinate system. It is defined in such a way that it transforms according to certain rules when changing coordinate systems.
What is the significance of the term 'covariant' in the context of this video?
-The term 'covariant' refers to the way certain objects, like basis vectors, transform when changing coordinate systems. It indicates that these objects vary in the same way as the coordinate system changes.
What is the role of the Jacobian in coordinate transformations?
-The Jacobian is a matrix of all first-order partial derivatives that defines the transformation rules between two coordinate systems. It is used to calculate how basis vectors and other tensor objects transform from one system to another.
How is the Jacobian related to the transformation of basis vectors?
-The Jacobian contains the factors that, when multiplied by the covariant basis vectors of one coordinate system, give the covariant basis vectors of the other coordinate system.
What is the difference between a covariant and a contravariant transformation?
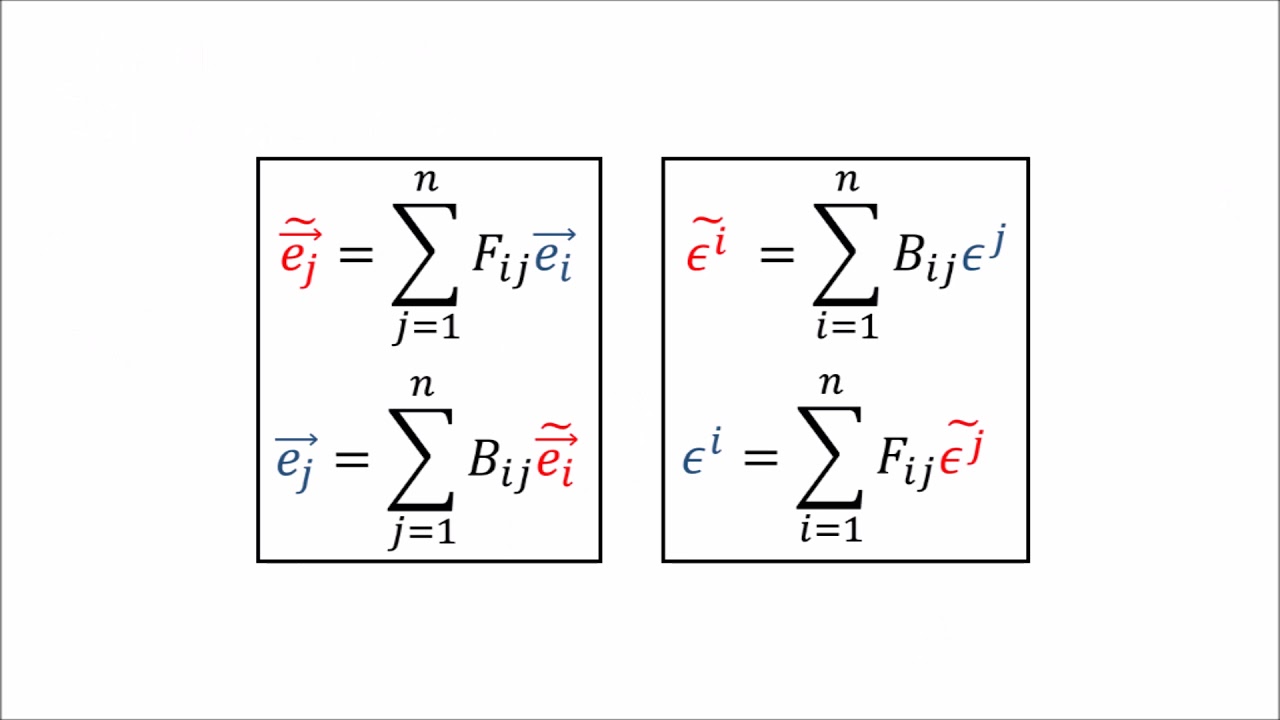
-A covariant transformation involves objects represented with lower indexes and uses the lower index of the Jacobian as a free index. A contravariant transformation involves objects represented with upper indexes and uses the upper index of the Jacobian as a free index.
Why are basis vectors considered to be covariant objects?
-Basis vectors are considered covariant objects because they transform according to the rules defined by the lower index of the Jacobian, which is indicative of covariant transformations.
How does the video script explain the concept of contravariant basis vectors?
-The script introduces the concept of contravariant basis vectors by showing how scalar factors in a linear combination, which are represented with upper indexes, transform according to contravariant rules, in contrast to the covariant basis vectors.
What is the importance of understanding both covariant and contravariant transformations in tensor calculus?
-Understanding both covariant and contravariant transformations is crucial in tensor calculus because almost every derivative object fits into one of these two categories, and knowing their transformation rules allows for correct calculations across different coordinate systems.
How does the script illustrate the concept of invariant objects in the context of vector transformations?
-The script illustrates invariant objects by showing that a vector, which is an invariant geometric object, can be expressed as a linear combination of covariant basis vectors and contravariant scalar factors, yielding the same result regardless of the coordinate system used.
Outlines
📚 Introduction to Vector Transformation and Covariant Basis Vectors
This paragraph introduces the topic of transforming vectors between coordinate systems, which was previously discussed in the context of coordinate value transformations. It sets the stage for the explanation of covariant basis vectors, which were defined in previous videos. The speaker clarifies the term 'covariant' and introduces the concept of using composite functions to explore these transformations. The paragraph also discusses the partial derivatives involved in transforming basis vectors from one coordinate system to another, highlighting the significance of the covariant basis in tensor calculus.
🔍 The Jacobian and Covariant Transformation
This section delves into the definition of the Jacobian, a key concept in coordinate transformations, which is represented with two free indices. The Jacobian is used to rewrite the expression for transforming covariant basis vectors from one system to another. It also introduces the idea of covariant transformations, where objects with lower indices transform according to specific rules involving the Jacobian. The paragraph emphasizes the importance of the position of indices in determining whether a transformation is covariant or contravariant.
🔄 Contravariant Transformation and Linear Combinations
Building upon the concept of covariant transformations, this paragraph explores contravariant transformations, which are represented with upper indices and use the upper index of the Jacobian for transformation. It discusses the invariant nature of vectors and how they can be expressed as linear combinations of basis vectors with scalar factors in both the unprimed and primed coordinate systems. The paragraph also establishes the relationship between covariant basis vectors, contravariant scalar factors, and the resulting invariant vector, leading to the definition of contravariant transformations.
📘 Summary of Jacobian, Covariant, and Contravariant Concepts
The final paragraph provides a comprehensive summary of the key concepts discussed in the video script. It defines the Jacobian in both the unprimed and primed systems, highlighting its role in transformations. It also distinguishes between covariant and contravariant transformations, emphasizing the importance of index positions. The paragraph concludes with an explanation of the terms 'covariant' and 'contravariant,' suggesting that they describe how objects vary in relation to coordinate transformations, and hints at the prevalence of these concepts in tensor calculus.
Mindmap
Keywords
💡Tensor Calculus
💡Coordinate Transformation
💡Covariant Basis Vectors
💡Composite Function
💡Partial Derivative
💡Jacobian
💡Covariant Transformation
💡Contravariant Transformation
💡Linear Combination
💡Invariant Object
Highlights
Introduction to transforming vectors from one coordinate system to another in tensor calculus.
Explanation of why basis vectors are called covariant basis vectors.
Definition and illustration of a covariant basis and its vectors.
Use of composite functions to understand coordinate transformations.
Differentiation of the function r with respect to z, introducing partial derivatives.
Introduction of the Jacobian as a key component in transformations.
The Jacobian's role in calculating the basis vectors in different coordinate systems.
Understanding how the basis vectors transform between coordinate systems.
Definition of covariant transformation and its significance in tensor calculus.
Explanation of contravariant transformation and its relationship to covariant transformation.
The importance of the position of indices in determining whether an object is covariant or contravariant.
The concept of an invariant object and its independence from coordinate systems.
Expression of a vector as a linear combination of basis vectors and scalar factors.
Transformation of the covariant basis vector from the prime system to the unprimed system.
Derivation of the scalar component transformation using the Jacobian.
The contravariant transformation rule and its application in tensor calculus.
The practical application of the Jacobian in transforming between coordinate systems.
Review of the major takeaways from the video, including the definition of the Jacobian and transformations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: