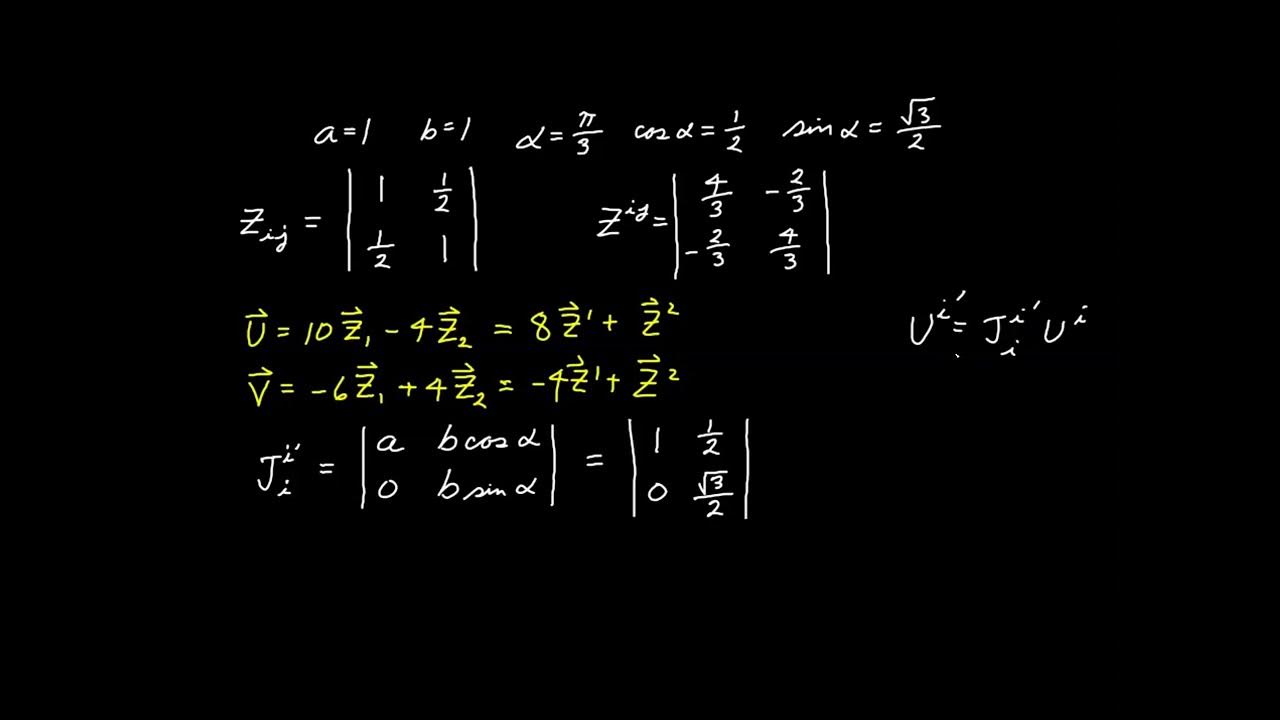Contravariant and Covariant Vectors | 2/2
TLDRThis educational video delves into the concepts of contravariant and covariant vector components, offering a mnemonic device to differentiate them by their indices. It explains the transformation laws for each, using the tangent vector of a parametric curve as an example for contravariant vectors and the gradient of a scalar field for covariant vectors. The video also touches on weighted contravariant vectors and the invariance of the inner product of contravariant and covariant vectors, emphasizing the importance of these mathematical objects in physics and coordinate transformations.
Takeaways
- 📚 Contravariant components transform in the opposite way as basis vectors under a change of coordinates.
- 🔤 Covariant components transform in the same manner as basis vectors under a change of coordinates.
- 🔠 Contravariant components are denoted by superscripts, while covariant components are denoted by subscripts.
- 🧠 A mnemonic to remember: the third letter in 'contravariant' is 'n' (points up), reminding you of superscripts. In 'covariant,' the third letter is 'v' (points down), reminding you of subscripts.
- 🔢 Contravariant vectors are tensors of Rank 1, and their components transform according to a specific transformation law involving partial derivatives.
- 🎯 The tangent vector to a parametric curve is an example of a contravariant vector because it follows the contravariant transformation law.
- ⚖️ Weighted contravariant vectors are a variation where a weight factor is included in the transformation law.
- 🔄 Covariant vectors follow a transformation law where the order of partial derivatives is reversed compared to contravariant vectors.
- 🧩 Gradient vectors, such as those derived from a scalar field, are an example of covariant vectors.
- 🔗 Invariant components, such as the inner product of a contravariant vector and a covariant vector, do not change under coordinate transformations and are fundamental in understanding tensors.
Q & A
What is the difference between contravariant and covariant vector components?
-Contravariant vector components transform in the opposite fashion compared to basis vectors under a change of coordinates, while covariant components transform in the same manner. Contravariant components are denoted with superscripts, and covariant components are denoted with subscripts.
How can you remember which index notation to use for contravariant and covariant components?
-For contravariant components, the third letter 'a' in 'contravariant' points up, reminding you to use superscripts. For covariant components, the third letter 'v' in 'covariant' points down, reminding you to use subscripts.
What is a contravariant vector in the context of tensor rank?
-A contravariant vector is a tensor of rank 1 whose components transform according to the law V^I_bar = V^r * (∂X^I_bar / ∂X^r), where the index r is summed over.
Can you provide an example of a contravariant vector?
-An example of a contravariant vector is the tangent vector to a parametric curve in a coordinate system. Its components transform according to the contravariant transformation law.
What is a weighted contravariant vector and how does it transform?
-A weighted contravariant vector is a variation where the components transform with a weight function W, following the law V^I_bar = W * V^r * (∂X^I_bar / ∂X^r).
What is the transformation law for covariant vector components?
-The transformation law for covariant vector components is U_I_bar = U_R * (∂X^R / ∂X_I_bar), with the order of partial derivatives switched compared to contravariant vectors.
How is the gradient of a scalar field related to covariant vectors?
-The gradient of a scalar field is a covariant vector, as its components U_I are partial derivatives of the scalar field with respect to each coordinate X^I, following the covariant transformation law.
What are invariant components or invariants in the context of coordinate transformations?
-Invariant components or invariants are mathematical objects that retain their value under a change of coordinates. Tensors themselves are invariant, and the inner product of a contravariant and a covariant vector is also an invariant.
Why are most vectors encountered in physics contravariant vectors?
-Most vectors in physics, such as displacement, velocity, and acceleration, are contravariant vectors because they transform in the same way as the basis vectors under a change of coordinates.
What is the significance of the inner product of a contravariant and a covariant vector?
-The inner product of a contravariant and a covariant vector is significant because it is an invariant, meaning it does not change under coordinate transformations and has an intrinsic value.
Outlines
📚 Contravariant and Covariant Vectors Explained
This paragraph introduces the concepts of contravariant and covariant vector components, highlighting their transformation behavior under coordinate changes. Contravariant components transform oppositely to basis vectors, indicated by superscripts, while covariant components transform similarly, denoted by subscripts. A memory aid is provided to help distinguish between the two based on the third letter of 'contravariant' and 'covariant'. The paragraph then sets up mathematical definitions by assuming a vector field on a subset of RN with two coordinate systems and explains the transformation law for contravariant vectors. An example of a contravariant vector is given through the tangent vector to a parametric curve in RN, illustrating its transformation law.
🔍 Covariant Vectors and Weighted Contravariant Vectors
This section delves into the definition and transformation law of covariant vectors, which differ from contravariant vectors by the order of partial derivatives in their transformation equation. It also introduces weighted contravariant vectors, which follow a modified transformation law influenced by a weight function. The paragraph uses the gradient of a scalar field as an example to demonstrate how covariant vectors transform under coordinate changes. The gradient vector's components are shown to adhere to the covariant transformation law, solidifying the concept that the gradient of a differentiable scalar field is inherently a covariant vector.
🔗 The Significance of Invariant Components
The final paragraph discusses invariant components, which are mathematical objects that retain their value during coordinate transformations. Tensors are highlighted as invariant objects, with their components transforming to maintain the tensor's intrinsic value. The inner product of a contravariant and a covariant vector is presented as an example of an invariant, which remains constant across different coordinate systems. The paragraph concludes with a note on the importance of invariants in the context of coordinate transformations, emphasizing their fundamental significance.
Mindmap
Keywords
💡Contravariant
💡Covariant
💡Tensor
💡Coordinate Transformation
💡Superscript and Subscript
💡Invariant Components
💡Partial Derivative
💡Parametric Curve
💡Gradient Vector
💡Differential Geometry
Highlights
Contravariance and covariance of vector components are explained with a memory aid involving the third letter of 'contravariant' and 'covariant'.
Contravariance is defined as the transformation of components in the opposite fashion to basis vectors under a change of coordinates.
Covariance is defined as the transformation of components in the same manner as basis vectors under a change of coordinates.
Contravariance is indicated by superscripts, while covariance is indicated by subscripts.
A mathematical definition of contravariant vectors is provided, involving the transformation law and the use of dummy indices.
An example of a contravariant vector is given through the tangent vector to a parametric curve in RN.
The transformation law for the tangent vector component is derived using the chain rule of differentiation.
Weighted contravariant vectors are introduced with a modified transformation law involving a weight function.
Covariance is defined with a different transformation law, where the order of partial derivatives is switched.
The gradient vector of a differentiable scalar field is shown to be a covariant vector following its transformation law.
The chain rule is used to derive the transformation of the gradient vector components under a coordinate change.
Most vectors in physics, such as displacement, velocity, and acceleration, are contravariant vectors.
The gradient vector is highlighted as a well-known example of a covariant vector in physics.
Invariant components or invariants are introduced as objects with intrinsic value unchanged under coordinate transformations.
Tensors are described as invariant objects, with the inner product of a contravariant and covariant vector being an example of an invariant.
The inner product's invariance under coordinate transformations is explained, drawing an analogy to the intrinsic value of temperature.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: