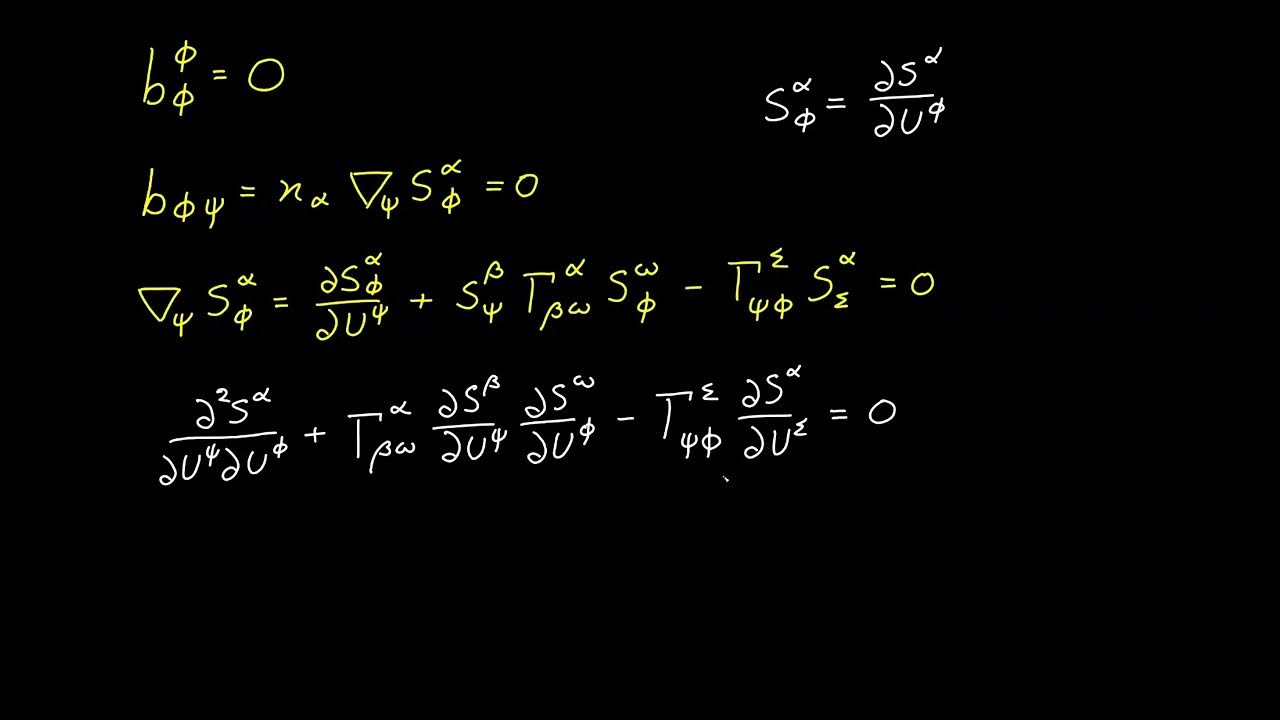Tensor Calculus 15: Geodesics and Christoffel Symbols (extrinsic geometry)
TLDRThis video delves into the concept of geodesics and Christoffel symbols within the realm of extrinsic geometry, focusing on 2D surfaces in 3D space. It introduces geodesics as the shortest path between two points on a curved surface, akin to straight lines in flat space. The script explains the physical significance of geodesics in general relativity, where they dictate the paths light travels in curved spacetime. The mathematical framework to identify and compute geodesics is explored, including the acceleration vector's relationship to the surface's normal and tangent vectors, leading to the formulation of the geodesic equation.
Takeaways
- 📚 The video introduces geodesics and Christoffel symbols in the context of extrinsic geometry, focusing on 2D surfaces in 3D space.
- 🔍 Geodesics are the shortest paths between two points on a curved surface, analogous to straight lines in flat space.
- 🌐 The concept of geodesics is crucial in understanding the Covariant derivative in tensor calculus, which will be discussed in future videos.
- 👨🏫 Additional resources for learning about geodesics are provided in the form of course notes linked in the video description.
- 🛰️ Geodesics have significant applications in physics, particularly in general relativity, where they describe the paths light takes in curved spacetime.
- 📏 To determine if a path is straight in flat space, one can check if the acceleration vectors are zero when traveling at constant speed.
- 🚀 On a curved surface, a geodesic is identified by acceleration vectors that are normal to the surface and have no tangential component.
- 📉 The video explains the mathematical difference between paths that are geodesics and those that are not, based on the orientation of acceleration vectors.
- 📈 The process of finding geodesics involves computing curves where the tangential acceleration is zero, using the surface's properties.
- 📘 Surfaces and curves are described using functions that map the 2D UV plane to 3D space, with curves on the surface parameterized by λ.
- 🔢 The acceleration vector along a curve is derived, involving partial derivatives and Christoffel symbols, which are essential for finding geodesics.
- 🧩 The video concludes with the derivation of the geodesic equation, which any curve satisfying is considered a geodesic, representing the 'straightest' path in curved space.
Q & A
What is the main focus of the video script?
-The video script focuses on introducing geodesics and Christoffel symbols in the context of extrinsic geometry, specifically within 2D surfaces living in 3D space, and their relation to the Covariant derivative in tensor calculus.
What is the significance of geodesics in physics?
-Geodesics are significant in physics, particularly in general relativity, as they represent the shortest path between two points in a curved spacetime, which is the path light follows around massive objects like stars and black holes.
How are geodesics defined in the context of the video?
-In the video, geodesics are defined as curves on a surface that have zero tangential acceleration when traveled along at a constant speed, meaning the acceleration vector points directly out of the surface in the normal direction.
What is the difference between a straight path in flat space and a geodesic on a curved surface?
-A straight path in flat space has zero acceleration when traveled at a constant speed, whereas a geodesic on a curved surface is the 'straightest' path that minimizes distance between two points and has only normal acceleration with no tangential component.
Why are Christoffel symbols important in the study of geodesics?
-Christoffel symbols are important because they help in determining the tangential components of the second-order derivative vectors, which are crucial in finding the geodesic curves where the tangential acceleration is zero.
What is the role of the second fundamental form in the context of geodesics?
-The second fundamental form, represented by the L_ij terms, provides the normal components of the second-order derivative with respect to the surface coordinates, which is essential in distinguishing between the tangential and normal components of acceleration.
How does the video script connect the concept of geodesics to the Covariant derivative in tensor calculus?
-The script mentions that understanding geodesics is the first step toward understanding the Covariant derivative, a key concept in tensor calculus, which will be discussed in a future video.
What is the Einstein summation convention used for in the script?
-The Einstein summation convention is used to simplify the expression for the acceleration vector along a curve by summing over repeated indices, making the formula more compact and easier to handle in calculations.
How are the metric tensor and its components used in the script?
-The metric tensor and its components are used to express the dot product of tangent vectors, which simplifies the process of solving for the Christoffel symbols and understanding the properties of the surface.
What is the geodesic equation derived in the script?
-The geodesic equation derived in the script is an equation where the tangential component of the acceleration vector is set to zero, which any curve satisfying this equation is a geodesic curve.
How does the script explain the process of finding geodesic curves on a surface?
-The script explains that to find geodesic curves, one must compute curves where the tangential acceleration is equal to zero by using the derived formula for the acceleration vector involving Christoffel symbols and the second fundamental form.
Outlines
📚 Introduction to Geodesics and Christoffel Symbols
This paragraph introduces the concepts of geodesics and Christoffel symbols within the context of extrinsic geometry, focusing on 2D surfaces in 3D space. The video aims to lay the groundwork for understanding the Covariant derivative in tensor calculus, a topic to be explored in future videos. Geodesics are defined as the shortest path between two points on a curved surface, analogous to a straight line in flat space. The paragraph also mentions the relevance of geodesics in general relativity, where light follows these paths in curved spacetime. The host suggests further study through a professor's course notes linked in the description.
🔍 Understanding Geodesics through Acceleration Vectors
The second paragraph delves into the physical interpretation of geodesics by examining the properties of velocity and acceleration vectors on both flat and curved surfaces. It explains that a straight path in flat space can be identified by zero acceleration when traveling at a constant speed, whereas on a curved surface, the challenge lies in finding a path with zero tangential acceleration, indicative of a geodesic. The paragraph distinguishes between paths that wander and those that move 'as straight as possible' in the forward direction on a curved surface, with the latter being a geodesic. It also introduces the mathematical difference between these paths, highlighting the role of normal and tangential vectors in defining geodesics.
📐 Mathematical Framework for Geodesics on Curved Surfaces
This paragraph establishes the mathematical framework necessary to compute geodesics on surfaces. It begins by reminding viewers of the process of mapping a 2D UV plane to a 3D space to form a surface, and how curves on this surface are created. The focus then shifts to the acceleration vector of a curve, derived from the second derivative of the position vector with respect to the curve parameter. The paragraph introduces the Christoffel symbols and the second fundamental form, which are essential for understanding how acceleration vectors decompose into normal and tangential components. The goal is to find curves where the tangential component of acceleration is zero, indicating a geodesic.
🧩 Decomposition of Acceleration Vector and Geodesic Detection
The fourth paragraph continues the mathematical development by discussing the decomposition of the acceleration vector into its tangential and normal components. It explains the use of the Einstein summation convention to simplify the expression for the acceleration vector and how the Christoffel symbols and the second fundamental form are derived. The paragraph also describes how to solve for these components by taking dot products with tangent and normal vectors, leading to the formula for the normal vector using cross products. The main objective is to express the acceleration vector in terms of known quantities, setting the stage for identifying geodesics where the tangential component of acceleration is zero.
🌐 The Geodesic Equation and its Physical Significance
In the final paragraph, the video concludes by summarizing the key points about geodesics. It reiterates that geodesics are the shortest paths in curved spaces, defined by having an acceleration vector that is purely normal to the surface, with no tangential component. The paragraph presents the geodesic equation, which is derived from setting the tangential component of the acceleration vector to zero. This equation is crucial for detecting geodesics and is highlighted as the path that light beams will follow in curved spacetime. The host encourages viewers to watch the next video for an example of applying the geodesic equation to find geodesics on a curved surface.
Mindmap
Keywords
💡Geodesics
💡Christoffel Symbols
💡Covariant Derivative
💡Extrinsic Geometry
💡Intrinsic Geometry
💡Tangent Vectors
💡Acceleration Vectors
💡General Relativity
💡Second Fundamental Form
💡Metric Tensor
💡Geodesic Equation
Highlights
Introduction to geodesics and Christoffel symbols in the context of extrinsic geometry.
Exploration of the shortest distance between two points on a curved surface, introducing the concept of geodesics.
Explanation of geodesics as the 'straightest possible path' in curved space, minimizing distance between points.
Connection between geodesics and general relativity, where space-time curvature affects the path of light.
Differentiation between geodesics and non-geodesic paths through the concept of acceleration vectors.
Description of how zero acceleration indicates a straight path in flat space when traveling at constant speed.
Analysis of acceleration vectors on curved surfaces and their implications for identifying geodesic curves.
Definition of a geodesic curve as one with zero tangential acceleration, normal to the surface.
Introduction of the mathematical framework for surfaces and curves in 3D space, using position vector R(U,V).
Derivation of the acceleration vector along a curve, involving Christoffel symbols and the second fundamental form.
Discussion on the importance of the second derivatives of the position vector R in determining the nature of a curve.
Introduction of the Einstein summation convention to simplify the expression of the acceleration vector.
Explanation of the second fundamental form components and their role in the normal components of the second order derivatives.
Derivation of the formula for Christoffel symbols, crucial for solving the geodesic equation.
Presentation of the geodesic equation, which describes curves with zero tangential acceleration.
Application of the geodesic equation in finding the paths that light follows in curved spacetime.
Summary of the video's content, emphasizing the significance of geodesics in both theoretical and practical contexts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: