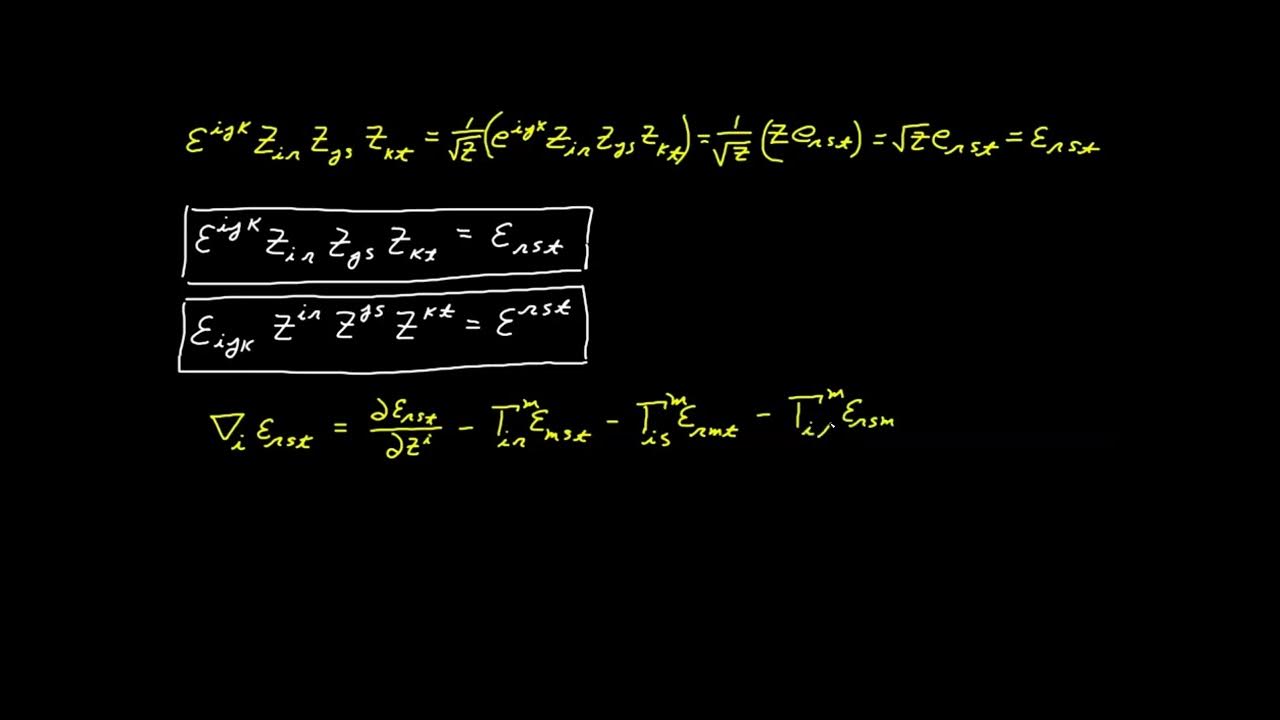Video 46 - Relative Tensors
TLDRThis video script explores the concept of tensors and their relationship with relative tensors, introducing the multiplication property of determinants. It demonstrates that if a tensor has one upper and one lower index, its determinant is a scalar function or tensor. The script also explains that permutation symbols are not tensors but relative tensors with specific weights, depending on the index positions. The video concludes by showing how the determinant of a tensor with two lower or upper indexes is a relative tensor of weight two or negative two, respectively.
Takeaways
- 📚 The script discusses the concept of tensors and introduces relative tensors as a larger class of objects that includes tensors as a subset.
- 🔍 It presents a modified expression for the determinant of a system with one upper and one lower index, highlighting the use of a new delta function.
- 🧩 The determinant of a second rank mixed tensor is shown to be a scalar function or a tensor itself, which is a key insight in tensor calculus.
- 📉 The script explains the multiplication property of determinants, which states that the product of the determinants of two tensors is equal to the determinant of their product.
- 📚 The proof of the multiplication property of determinants is demonstrated using tensor calculus, showing its power and utility over traditional linear algebra methods.
- 🔑 The transformation rules for permutation symbols are derived, revealing that they are not tensors but relative tensors due to the presence of Jacobian factors.
- 🔄 The concept of 'weight' in relative tensors is introduced, with the weight being the exponent of the Jacobian factor in their transformation rules.
- 📈 The determinant of a tensor with two covariant indices (both lower) is shown to be a relative tensor of weight +2, while with two contravariant indices (both upper) it is of weight -2.
- 📝 The script emphasizes that whether the determinant of a tensor is a tensor itself depends on the position of the indices, distinguishing between absolute and relative tensors.
- 🔮 The importance of understanding the transformation properties of tensors and relative tensors is underscored for their application in various mathematical and physical contexts.
Q & A
What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to explore the concept that tensors are a subset of a larger class of objects known as relative tensors, and to discuss the determinant of a second rank mixed tensor.
What is the significance of the delta function introduced in the video?
-The delta function is significant because it is equivalent to the product of permutation symbols and allows for a more concise expression of the determinant, which is essential in proving that the determinant of a tensor is also a tensor under certain conditions.
How does the video demonstrate that the determinant of a second rank mixed tensor is a tensor?
-The video demonstrates this by showing that if aij is a tensor, then the factors in the determinant expression are tensors, and since the determinant involves a full contraction, it results in a scalar function, which is a tensor invariant across coordinate systems.
What is the multiplication property of determinants discussed in the video?
-The multiplication property of determinants states that the product of the determinants of two tensors is equal to the determinant of the product of those two tensors when contracted in a specific way.
How does the video prove the multiplication property of determinants using tensor calculus?
-The video proves the multiplication property by substituting the expression for a tensor aij as a contraction of two other tensors b and c, and then showing that the determinant of a is equivalent to the product of the determinants of b and c.
What are relative tensors, and how do they differ from absolute tensors?
-Relative tensors are objects that transform with the usual Jacobian factors like normal tensors but also have an additional factor of the Jacobian. They are classified according to the exponent of the Jacobian factor, known as the weight. Absolute tensors, which have been the focus of the series so far, are relative tensors with a weight of zero.
Why are permutation symbols not considered tensors?
-Permutation symbols are not considered tensors because their transformation rules involve additional Jacobian factors that do not satisfy the criteria for tensor transformation, indicating they are relative tensors with non-zero weights.
What is the weight of a relative tensor, and how is it determined?
-The weight of a relative tensor is the exponent of the Jacobian factor in its transformation rule. It is determined by the presence of additional Jacobian factors in the transformation of the tensor.
How does the determinant of a tensor with two covariant indexes transform?
-The determinant of a tensor with two covariant indexes (both on the bottom) is a relative tensor of weight two, as shown by the transformation rule derived in the video.
What is the relationship between the determinant of the Jacobian and its inverse?
-The determinant of the Jacobian and its inverse are reciprocals of each other, meaning their product is equal to one. This is a special case of the multiplication property of determinants.
How does the video conclude about the determinant of a tensor with two indexes in different positions?
-The video concludes that whether the determinant of a tensor is itself a tensor depends on the location of the indexes. If the indexes are mixed (one upper and one lower), the determinant is an invariant scalar (a tensor of rank zero). If both indexes are on the bottom (covariant), the determinant is a relative tensor of weight two, and if both are on the top (contravariant), it is a relative tensor of weight negative two.
Outlines
🧠 Tensors and the Delta Function
This paragraph introduces the concept of tensors as a subset of relative tensors and explores the delta function's role in expressing the determinant of a second rank mixed tensor concisely. It explains how if a tensor is involved in the determinant calculation, the result is also a tensor, leading to the determinant being a scalar function. The paragraph also discusses the transformation of the determinant expression in different coordinate systems.
🔍 The Multiplication Property of Determinants
The second paragraph delves into an important property of determinants, demonstrating that the product of the determinants of two tensors is equal to the determinant of their product. This property is not limited to tensors but is proven using tensor calculus, showcasing its utility over traditional linear algebra methods. The paragraph also sets the stage for further investigation into the determinants of tensors with different index configurations.
📚 Transformation Rules and Relative Tensors
Here, the script discusses the transformation rules for permutation symbols and the concept of relative tensors. It explains that permutation symbols do not transform as tensors due to additional Jacobian factors in their transformation rules, leading to the introduction of relative tensors, which have a weight determined by the exponent of the Jacobian factor. The paragraph also clarifies the difference between absolute tensors (relative tensors with weight zero) and relative tensors.
🔗 Deriving Transformation Rules for Determinants
The fourth paragraph focuses on deriving the transformation rules for determinants of tensors with two lower indexes, revealing that these determinants are relative tensors of weight two. It goes through the process of expressing the relationship in a primed system, substituting the transformation rules, and simplifying the expression to show the determinant's transformation properties.
📉 Determinants and Tensor Index Positions
This section examines how the position of tensor indexes affects whether the determinant of a tensor is itself a tensor. It establishes that a second rank mixed tensor with one upper and one lower index has a determinant that is a scalar function, while tensors with two indexes in the same position (either both upper or both lower) result in relative tensors with weights of plus two or negative two, respectively.
🔚 Recap and Conclusion on Tensor Determinants
The final paragraph provides a recap of the video's main points, emphasizing the determinant's properties in relation to tensors. It reiterates the multiplication property of determinants, the proof that the determinant of a tensor is a scalar if the tensor has mixed indexes, and the special case of the determinants of the Jacobian and its inverse being reciprocals. The paragraph concludes with the observation that the determinant of a tensor being a tensor itself depends on the index positions.
Mindmap
Keywords
💡Tensor
💡Relative Tensors
💡Permutation Symbols
💡Determinant
💡Full Contraction
💡Delta Function
💡Jacobian
💡Scalar Function
💡Mixed Tensor
💡Multiplication Property of Determinants
💡Absolute Tensor
Highlights
Tensors are a subset of a larger class of objects known as relative tensors.
The delta function is equivalent to the product of permutation symbols in a specific combination.
A determinant can be expressed more concisely using the newly defined delta function.
If aij is a tensor, then the determinant of a second rank mixed tensor is also a tensor.
The determinant of a tensor can be represented in a scalar function form.
The determinant of a second rank mixed tensor is invariant across coordinate systems.
A tensor aij can be expressed as a contraction of two other mixed rank tensors b i k and c k j.
The multiplication property of determinants states that the product of determinants equals the determinant of the product.
The proof of the multiplication property of determinants demonstrates the utility of tensor calculus.
The determinant of a tensor with two lower indexes is a relative tensor of weight two.
Permutation symbols eijk do not transform as tensors due to additional jacobian factors.
Relative tensors transform with usual jacobian factors and an additional jacobian factor.
The weight of a relative tensor is determined by the exponent of the jacobian factor.
Absolute tensors are relative tensors with a weight of zero.
The determinant of a second rank tensor with two indexes on the bottom is not an invariant expression but a relative tensor.
The determinant of the jacobian and its inverse are reciprocals of each other.
The transformation rules for permutation symbols lead to the understanding of relative tensors.
The location of indexes determines whether the determinant of a tensor is itself a tensor.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: