Tensor Calculus 16: Geodesic Examples on Plane and Sphere

eigenchris

19 Sept 201820:54

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video explores the concept of geodesics, the shortest paths on curved surfaces, building on the foundation of Christoffel symbols and the second fundamental form. The script corrects a common misconception about geodesics being the shortest distance, emphasizing their nature as 'straightest paths' on a surface. It demonstrates the calculation process for geodesics on a flat plane and a sphere, highlighting the simplification when Christoffel symbols are zero and the special case of great circles on a sphere being geodesics, providing an intuitive understanding of these mathematical paths.

Takeaways

📚 The video is a continuation of a series on geodesics and Christoffel symbols, so it's important to watch the previous video for context.
🛤️ Geodesics are the straightest possible paths on a curved surface, defined by having zero acceleration tangential to the surface when moving at a constant speed.
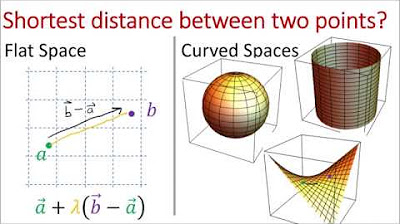
🔍 A mistake from the previous video is corrected: geodesics do not always represent the shortest distance between two points on a surface.
🔑 The process for finding geodesics involves two main steps: calculating Christoffel symbols and solving the geodesic equation with these symbols.
📉 The Christoffel symbols are crucial as they provide information about how basis vectors change from point to point on the surface.
📏 The geodesic equation simplifies when all Christoffel symbols are zero, as in the case of a flat plane, leading to linear solutions for the path coordinates.
📈 For the flat plane example, the geodesic equation results in straight lines, confirming the sanity check for the method.
🌐 The sphere example involves more complex calculations, including derivatives of the position vector and the metric tensor.
🔢 The sphere's metric tensor is diagonal, simplifying the computation of its inverse, which is essential for calculating Christoffel symbols.
⭕ The only non-zero Christoffel symbols for the sphere are related to the change in basis vectors along the latitude and longitude, leading to specific geodesic equations.
🌍 For the sphere, the equator and all great circles (circles with the center at the sphere's center) are geodesics, which aligns with the intuitive understanding of 'straight' paths on a sphere.

Q & A

What are geodesics and why are they important in the context of curved surfaces?
-Geodesics are the straightest possible paths that can be drawn on a curved surface. They are important because they represent the shortest or most direct routes on such surfaces, akin to straight lines in flat spaces.
What is the formal definition of a geodesic curve?
-A geodesic curve is defined as a curve on which there is zero acceleration tangential to the surface when traveling along the curve at a constant speed. The acceleration vector is completely normal to the surface.
Why is it incorrect to think of geodesics as always providing the shortest distance between two points on a curved surface?
-While geodesics can sometimes provide the shortest distance, such as on a sphere, they are not always the shortest path. For example, a path around a sphere in the opposite direction is also a geodesic, but not the shortest path. It's more accurate to consider geodesics as paths traced by moving straight ahead on a curved surface.
What are the two main steps involved in computing geodesics on a surface?
-The two main steps are: 1) Calculating the Christoffel symbols, which provide information about how basis vectors change from point to point on the surface, and 2) Plugging the Christoffel symbols into the geodesic equation and solving for the path, which is a set of coordinates as a function of the path parameter.
Why are the Christoffel symbols set to zero for geodesics on a flat plane?
-On a flat plane, the basis vectors do not change from point to point, hence the Christoffel symbols, which track changes in basis vectors, are zero. This is because there is no curvature, and the tangent vectors to the coordinate curves are constant.
What is the significance of the geodesic equation becoming simpler when all Christoffel symbols are zero?
-When all Christoffel symbols are zero, the geodesic equation simplifies to stating that the second-order derivative along the curve is zero, indicating no acceleration. This simplification makes it easier to solve and confirms that straight lines are geodesics in flat spaces.
How do the geodesic equations for a sphere differ from those of a flat plane?
-For a sphere, the geodesic equations are nonlinear and coupled differential equations, which are more complex to solve compared to the flat plane's equations. The complexity arises due to the curvature of the sphere and the need to account for the changing basis vectors.
What is a great circle on a sphere and why are all great circles geodesics?
-A great circle on a sphere is a circle whose center coincides with the center of the sphere. All great circles are geodesics because they represent the shortest path between any two points on the sphere, and their curvature aligns with the sphere's surface, ensuring the acceleration vector is always normal to the surface.
Why are only the equator and other great circles geodesics on a sphere, and not other circles of latitude?
-The equator and other great circles are geodesics because their paths ensure the acceleration vector points directly towards the sphere's center, which is normal to the surface. In contrast, other circles of latitude have an acceleration vector that also has a tangential component, disqualifying them as geodesics.
What is the process for computing geodesics on a general curved surface?
-The process involves two main steps: first, compute the Christoffel symbols for the surface, which requires calculating first and second derivatives of the position vector and the inverse metric tensor; second, solve the geodesic equations using the computed Christoffel symbols. This process can be complex and often requires advanced mathematical techniques.

Outlines

00:00

📚 Introduction to Geodesics on Curved Surfaces

This paragraph introduces the concept of geodesics as the straightest paths on a curved surface, continuing from a previous video. It corrects a common misconception that geodesics are always the shortest path, instead emphasizing they represent the path of constant forward motion. The formal definition involves zero tangential acceleration. The process for finding geodesics involves calculating Christoffel symbols and solving the geodesic equation, which is simplified when the surface is a flat plane, leading to the conclusion that geodesics on a flat plane are straight lines.

05:00

🔍 Calculating Geodesics on a Flat Plane

The second paragraph delves into the specifics of calculating geodesics on a flat plane, using the geodesic equation with all Christoffel symbols equal to zero. This results in second-order derivatives of the curve's parameters being zero, leading to linear solutions for these parameters. The summary explains that the geodesic curves on a flat plane can be represented by linear equations, confirming that straight lines are indeed geodesics in this context, and highlighting the importance of initial position and velocity in defining a unique geodesic.

10:01

🌐 Deriving Christoffel Symbols for a Sphere

This paragraph focuses on the derivation of Christoffel symbols for a sphere, a more complex surface than a flat plane. It involves calculating first and second derivatives of the position vector, the metric tensor, and its inverse. The process is detailed, including the computation of tangent vectors along the sphere's parameters and the simplification using the Cartesian coordinate system. The result is a set of Christoffel symbols, some of which are zero due to the sphere's symmetry, leading to a simplified set of equations for the geodesics on the sphere.

15:04

🧭 Solving Geodesic Equations for a Sphere

The fourth paragraph discusses solving the geodesic equations for a sphere, starting with the special case of a circle of latitude. It simplifies the problem by considering only the equator, where the latitude is a constant, and longitude varies linearly with a parameter. The paragraph explains that the geodesic equations reduce to a condition that the derivative of the latitude with respect to the parameter must be zero, which is true for the equator. This confirms that the equator is a geodesic on the sphere, while other circles of latitude are not.

20:06

🌍 Generalizing Geodesics on a Sphere

The final paragraph generalizes the findings for the sphere, concluding that all great circles, which are circles with the center at the sphere's center, are geodesics. This aligns with the intuitive understanding of 'straight' paths on a sphere. The summary emphasizes the process of computing geodesics, which involves calculating Christoffel symbols and solving the geodesic equations, and notes that while this can be challenging for general surfaces, explicit formulas can be found for simple surfaces like the sphere without computational assistance.

Mindmap

Keywords

💡Geodesics

Geodesics are the shortest paths between two points on a curved surface, analogous to straight lines on a flat surface. In the video, geodesics are defined as curves with zero acceleration tangential to the surface when traveled at constant speed. The concept is central to the video's theme, as it explains how to find these paths on various surfaces, such as planes and spheres.

💡Christoffel Symbols

Christoffel symbols are mathematical objects used in differential geometry to describe how basis vectors change as one moves over a curved surface. The video explains that computing these symbols is a crucial step in finding geodesics, as they are plugged into the geodesic equation to solve for the path on the surface.

💡Acceleration Vector

The acceleration vector is a key concept in the video's explanation of geodesics. It is defined as the rate of change of velocity of a point moving along a curve. For a path to be a geodesic, the tangential component of this vector must be zero, meaning all acceleration is normal to the surface.

💡Tangential Components

In the context of the video, tangential components refer to the parts of a vector that are parallel to the surface. The script emphasizes that for a curve to be a geodesic, the tangential components of the acceleration vector must be zero, indicating no change in the direction of motion along the surface.

💡Second Fundamental Form

The second fundamental form is a measure of how a surface bends or curves. Although not explicitly defined in the script, it is implied to be part of the formula for the acceleration vector along a curve, which is essential for deriving the geodesic equation.

💡Metric Tensor

The metric tensor is a mathematical object that provides a way to measure distances and angles on a surface. In the video, the components of the inverse metric tensor are necessary for calculating the Christoffel symbols, which in turn are used to find geodesics.

💡First and Second Derivatives

First and second derivatives of the position vector with respect to the surface coordinates are required to compute the Christoffel symbols and the geodesic equation. The script mentions that first derivatives give the tangent vectors to the coordinate curves on the surface, while second derivatives are involved in the calculation of the Christoffel symbols.

💡Flat Plane

The flat plane is used as an example in the video to illustrate the concept of geodesics. It is a simple case where geodesics are just straight lines. The script explains that on a flat plane, all Christoffel symbols are zero, leading to a straightforward geodesic equation.

💡Sphere

The sphere is another surface example used in the video to demonstrate the computation of geodesics. The script discusses the parametric equations of a sphere, the calculation of its Christoffel symbols, and the geodesic equations. It is shown that great circles on a sphere are geodesics, which aligns with the intuitive idea of 'straight' paths on a globe.

💡Equator

In the context of the sphere example, the equator is highlighted as a special case of a geodesic. The script explains that traveling along the equator is a geodesic path because the acceleration vector points directly towards the center of the sphere, which is consistent with the definition of geodesics.

💡Great Circles

Great circles are circles on the surface of a sphere that have the same center as the sphere itself. The video concludes that all great circles on a sphere are geodesics, which is a significant finding derived from the process of computing geodesics using Christoffel symbols and the geodesic equation.

Highlights

Introduction to the concept of geodesics as the straightest possible paths on a curved surface.

Clarification of a previous mistake regarding the shortest distance between two points on a curved surface, emphasizing that geodesics are not always the shortest path.

Explanation of the formal definition of a geodesic curve with zero acceleration tangential to the surface.

Overview of the process for computing geodesics on a surface, involving calculating Christoffel symbols and solving the geodesic equation.

Demonstration of the computation of Christoffel symbols for a flat plane, resulting in zero values due to the constant basis vectors.

Solution of the geodesic equation for a flat plane, revealing that geodesics are straight lines.

Introduction of the second example involving geodesics on a sphere of radius one.

Derivation of the parametric formulas for the sphere and the calculation of tangent vectors along the U and V curves.

Explanation of the metric tensor for the sphere and its role in computing the Christoffel symbols.

Calculation of the second derivatives of the position vector for the sphere and their significance in determining the Christoffel symbols.

Derivation of the inverse metric tensor for the sphere, simplifying the computation of the Christoffel symbols.

Identification of non-zero Christoffel symbols for the sphere, which are crucial for solving the geodesic equations.

Simplification of the geodesic equations for the sphere by considering the special case of a circle of latitude.

Discovery that the equator is a geodesic on the sphere, providing the shortest path between two points on the equator.

Conclusion that all great circles on the sphere are geodesics due to spherical symmetry.

Summary of the process for computing geodesics on a curved surface and the challenges involved.

Highlight of the practical application of geodesic computation for simple surfaces like the sphere without the need for computers.

Transcripts

Browse More Related Video

Tensor Calculus 15: Geodesics and Christoffel Symbols (extrinsic geometry)

Video 95 - Geodesic Curves

The Mathematics of our Universe

Tensor Calculus 17: The Covariant Derivative (flat space)

Tensor Calculus 19: Covariant Derivative (Intrinsic) and Geodesics

Tensor Calculus 18: Covariant Derivative (extrinsic) and Parallel Transport

Related Tags

Geodesics Christoffel Symbols Surfaces Flat Plane Sphere Differential Equations Tangent Vectors Metric Tensor Tensor Calculus Geometric Paths Mathematical Analysis