The Mathematics of our Universe

Zach Star

24 Jul 201922:53

EducationalLearning

32 Likes 10 Comments

TLDRThis video explores the concept of dimensions, delving into the fourth dimension of time and Einstein's space-time theory, which unifies space and time as a single entity warped by mass. It explains Gaussian curvature and its implications for the shape of the universe, introduces geodesics as the shortest paths on curved surfaces, and discusses the metric tensor's role in measuring distances in curved spaces. The script concludes by highlighting the educational platform Brilliant, which offers interactive courses to deepen understanding of these complex topics.

Takeaways

📏 We experience three spatial dimensions in everyday life, allowing movement in left-right, up-down, and forward-backward directions.
⏰ Time is considered the fourth dimension, essential for specifying events in the universe, and is distinct from spatial dimensions as it is a temporal dimension.
🔗 Einstein's theory of relativity links space and time into a single construct called space-time, where massive objects curve space-time, affecting distances and times.
🔍 The curvature of space-time has real-world implications, such as time passing differently on various planets and the bending of light around massive objects.
📘 The equations of general relativity relate the geometry of space-time to mass and energy, encapsulated by John Wheeler's phrase that 'space-time tells matter how to move and matter tells space-time how to curve'.
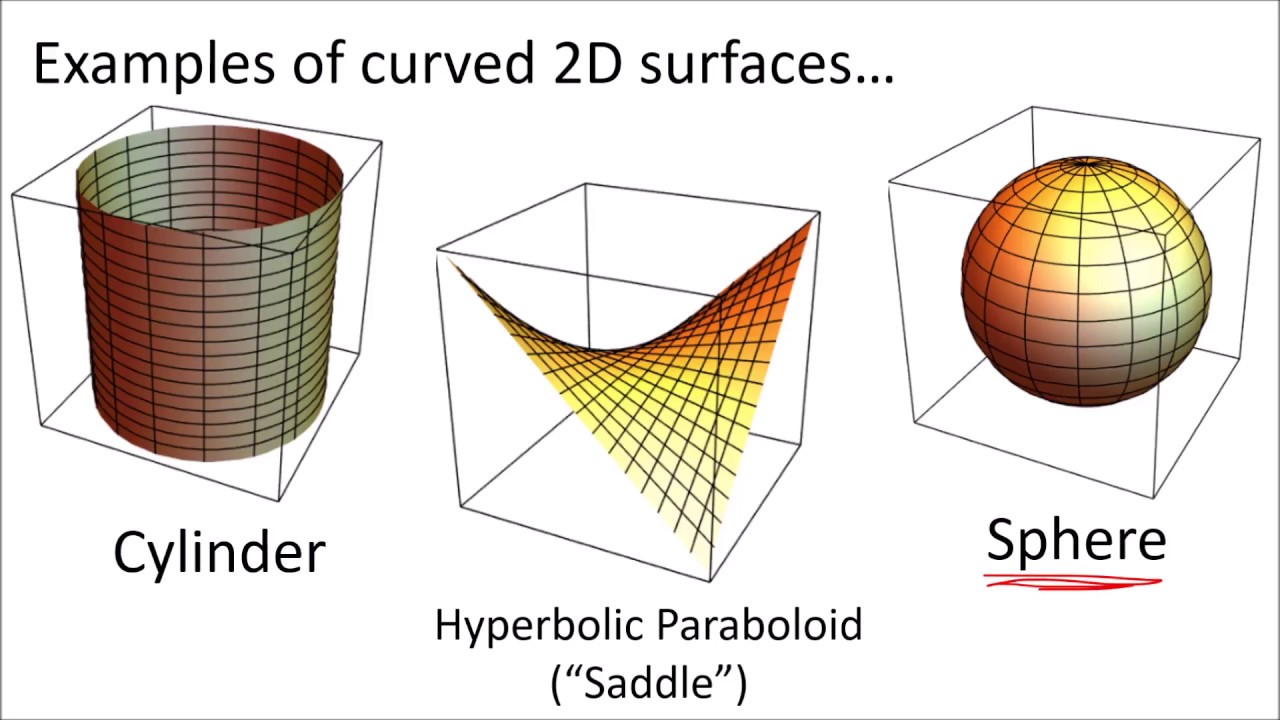
🧰 Gaussian curvature is a measure of the curvature of a surface, which can be positive (like a sphere), negative (like a saddle), or zero (like a flat plane or cylinder).
🌐 Gauss's Theorema Egregium reveals that the Gaussian curvature of a surface remains unchanged under smooth deformation, explaining why a flat piece of paper can wrap around a cylinder without wrinkles.
🌍 Determining the shape of the Earth or other surfaces can be achieved by observing the relationship between the circumference and radius of circles drawn on the surface, indicative of the surface's curvature.
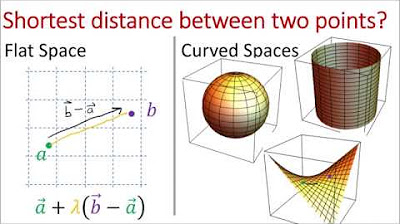
🛤️ Geodesics are the shortest paths between two points on a curved surface, like the great circles on a sphere, and are the paths light takes to minimize travel time.
📐 The metric tensor is a mathematical tool for calculating distances on curved surfaces and is fundamental to Einstein's general theory of relativity, describing the curvature of space-time.
🚀 General relativity redefined our understanding of gravity, proposing that gravity is not a force but a result of the curvature of space-time, with objects moving along straight lines in this curved space-time.

Q & A

What are the three spatial dimensions we experience in everyday life?
-The three spatial dimensions we experience in everyday life are left to right, up and down, and forward and back.
Why is time considered the fourth dimension?
-Time is considered the fourth dimension because it is an additional value needed to completely specify an event in the universe, alongside the three spatial dimensions.
How does Einstein's general theory of relativity relate space and time?
-Einstein's general theory of relativity states that massive objects curve space-time, linking space and time together and showing that they are not independent but are in fact interconnected.
What are the consequences of space-time curvature caused by massive objects?
-The curvature of space-time by massive objects leads to phenomena such as time ticking differently on different planets and massless photons being bent by massive objects.
What is Gaussian curvature and why is it significant?
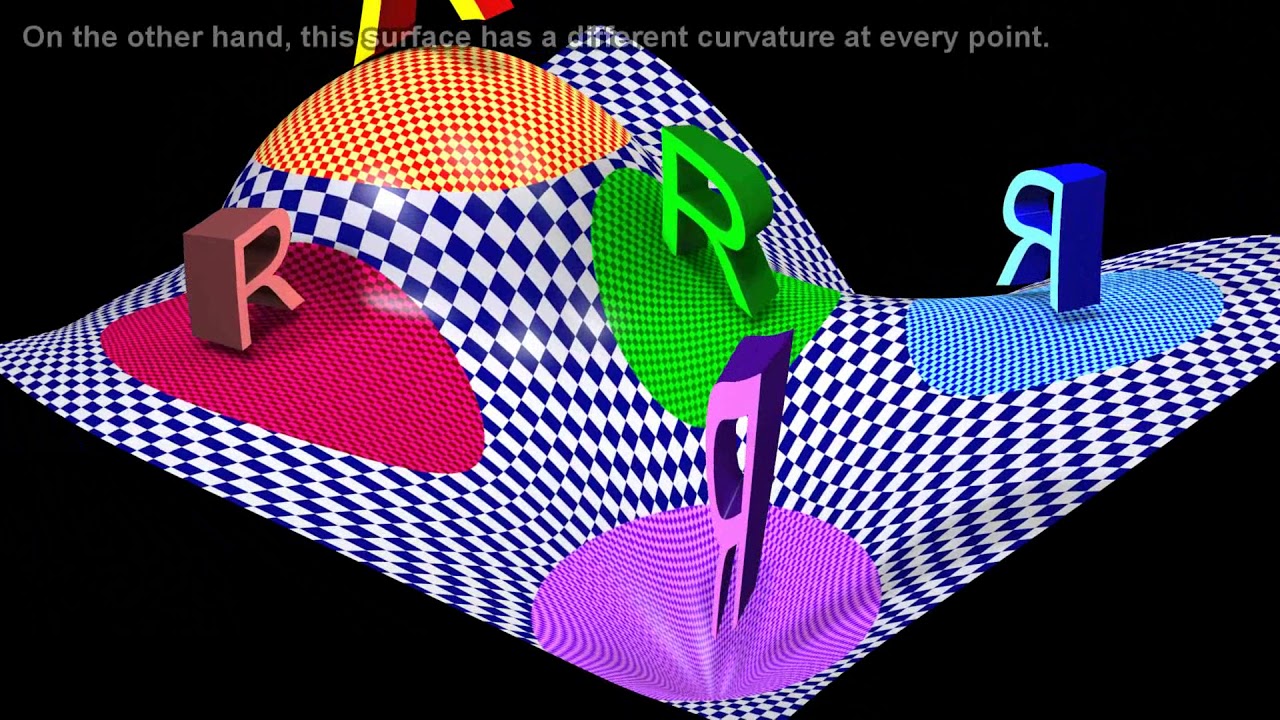
-Gaussian curvature is a measure of the curvature of a surface at a particular point, taking into account the curvature in two perpendicular directions. It is significant because it helps determine the intrinsic curvature of a surface and is a key concept in understanding non-Euclidean geometry.
How does the Gaussian curvature of a sphere differ from that of a flat surface or a saddle shape?
-A sphere has positive Gaussian curvature because both perpendicular segments curve outwards, while a flat surface has zero Gaussian curvature as both segments are flat. A saddle shape, on the other hand, has negative Gaussian curvature because one segment curves outwards and the perpendicular segment curves inwards.
What does the theorem of Gauß-Bonnet state?
-The Gauß-Bonnet theorem states that if you smoothly deform a surface, its Gaussian curvature at any point will not change. This means that surfaces with the same Gaussian curvature can be smoothly deformed into each other without introducing wrinkles or distortions.
How can one determine if they are on a curved surface without leaving it?
-One can determine if they are on a curved surface by measuring the circumference of a circle with a known radius. If the surface is curved, the circumference will deviate from the expected value of 2πr, indicating the presence of curvature.
What is a geodesic and why is it important in understanding curved surfaces?
-A geodesic is the shortest path between two points on a curved surface. It is important because it represents the path that light or an object would naturally take to minimize travel time, which is not necessarily a straight line on a curved surface.
What is the metric tensor and how does it relate to the curvature of space?
-The metric tensor is a mathematical tool that describes the distances between points on a curved surface or space-time. It is essential in general relativity as it allows for the calculation of distances in a curved space and contributes to the description of space-time curvature.
How does the concept of geodesics relate to the way light travels in the universe?
-Light travels along geodesics, which are paths of shortest time rather than shortest distance. When light moves through a vacuum, it travels in straight lines, which are geodesics in flat space. However, around massive objects, light bends, following geodesics that are no longer straight lines, indicating the curvature of space.

Outlines

00:00

🌌 Understanding Space-Time and the Fourth Dimension

This paragraph introduces the concept of dimensions, explaining the three spatial dimensions we experience daily and the necessity of a fourth temporal dimension, time, to specify events in the universe. It discusses Einstein's theory of relativity, which unifies space and time into a single construct called space-time, and how massive objects curve space-time, affecting the passage of time and the path of light. The paragraph also touches on the mathematics behind space-time curvature, highlighting the relationship between geometry, mass, and energy as described by physicist John Wheeler.

05:01

📏 Exploring Gaussian Curvature and its Implications

The second paragraph delves into the concept of Gaussian curvature, contrasting the common understanding of curvature with the mathematical definition. It uses examples like a piece of paper, a sphere, and a saddle to illustrate positive, zero, and negative Gaussian curvature, respectively. The paragraph explains how Gaussian curvature is calculated and the significance of this property in determining the shape and properties of different surfaces. It also introduces the theorem of Gauß, which states that Gaussian curvature remains consistent through smooth deformations of a surface.

10:04

🌐 Living on Curved Surfaces: Detecting Curvature Without Leaving

This paragraph explores the idea of living on curved surfaces and how inhabitants might detect the curvature of their environment without leaving it. It suggests methods such as measuring the circumference of a circle with a known radius to infer the surface's curvature. The paragraph also discusses the behavior of parallel lines on different surfaces and how the internal angles of triangles can indicate the nature of the surface's curvature. It touches on the implications of these concepts for understanding the shape of our universe.

15:06

🛫 Geodesics, Light Paths, and the Metric Tensor

The fourth paragraph discusses geodesics, the shortest paths between two points on a curved surface, using the example of flight paths that follow great circles on the Earth. It explains how light travels along these geodesics to minimize travel time, bending around massive objects due to the curvature of space-time. The paragraph introduces the metric tensor, a mathematical tool that describes the distance between points on curved surfaces and is essential for understanding the curvature of space-time in Einstein's general theory of relativity.

20:09

🔍 The Impact of General Relativity on Our Understanding of Gravity

In the final paragraph, the video script explains how general relativity revolutionized our concept of gravity, redefining it not as a force but as a curvature of space-time caused by mass. It describes the motion of objects, such as a ball thrown in the air, as following straight lines in space-time, which appear parabolic due to the curvature caused by Earth's mass. The paragraph emphasizes the deep mathematical foundations of our universe and hints at further exploration of these concepts in upcoming content.

🚀 Conclusion and Promotion of Educational Resources

The concluding paragraph summarizes the video's content and promotes Brilliant.org, an educational platform offering interactive math and science courses. It highlights the platform's hands-on approach to learning and its coverage of advanced topics relevant to the video's themes, such as astronomy, geodesics, non-Euclidean geometry, dark matter, and black holes. The paragraph offers a discount for viewers interested in subscribing to Brilliant's premium service and encourages engagement with the content through likes, subscriptions, and social media following.

Mindmap

Keywords

💡Spatial dimensions

Spatial dimensions refer to the measurable extents of the universe in which we exist and move. In the video, it's mentioned that we experience three spatial dimensions—left to right, up and down, and forward and back. These dimensions are foundational to understanding the physical world and are integral to the concept of space-time, which combines these spatial dimensions with time as the fourth dimension.

💡Temporal dimension

The temporal dimension is the concept of time as a dimension, separate from the three spatial dimensions. It is described in the video as not extending beyond height, length, and width but rather existing as a dimension that influences the timing of events. Time is essential for specifying an event in the universe, and its unique characteristic is that it cannot be visualized or pointed to like the spatial dimensions.

💡Space-time

Space-time is the four-dimensional continuum that combines the three spatial dimensions with the temporal dimension of time. The video explains that Einstein's general theory of relativity describes space-time as being弯曲的 by massive objects, leading to phenomena such as time dilation and the bending of light. Space-time is central to understanding how gravity works in the universe, as it is the fabric that objects move through.

💡Curvature

Curvature in the context of the video refers to the bending or warping of space-time caused by massive objects. It is a key concept in Einstein's theory of general relativity and is illustrated through the effects on time and the path of light. The video explains how curvature affects distances and times between events, leading to observable phenomena like the bending of light around massive objects.

💡Gaussian curvature

Gaussian curvature is a measure of the curvature of a surface at a particular point, taking into account the curvature in two perpendicular directions. The video uses the concept of Gaussian curvature to explain how different surfaces, such as a sphere or a saddle shape, can have positive or negative curvature, which affects their geometric properties and how they can be mapped onto each other without distortion.

💡Geodesics

Geodesics are the shortest paths between two points on a curved surface, analogous to straight lines on a flat surface. The video describes how geodesics, like the great circles on a sphere, are the paths that light follows to minimize travel time, which is integral to understanding how light behaves in the presence of massive objects and the resulting curvature of space-time.

💡Metric tensor

The metric tensor is a mathematical object that describes the geometry of a surface, allowing for the calculation of distances between points on curved surfaces. In the video, it is explained as a tool that generalizes the Pythagorean theorem to non-flat spaces, providing the necessary corrections to measure distances in the presence of curvature, which is crucial for understanding space-time in general relativity.

💡General theory of relativity

Einstein's general theory of relativity is a theory of gravitation that describes gravity not as a force but as a curvature of space-time caused by mass and energy. The video outlines how this theory revolutionized our understanding of gravity, showing how objects move along geodesics in curved space-time, which is perceived as the force of gravity.

💡Non-Euclidean geometry

Non-Euclidean geometry refers to geometrical studies that take place on surfaces that are not flat, such as spheres or saddle shapes. The video discusses how non-Euclidean geometry is essential for understanding the universe's large-scale structure and the behavior of objects on these curved surfaces, including the angles of triangles and the properties of geodesics.

💡Cosmic Microwave Background

The Cosmic Microwave Background (CMB) is the thermal radiation left over from the early universe, shortly after the Big Bang. The video mentions that scientists have used observations of the CMB to determine that the universe is mostly flat, with parallel lines behaving as expected in the absence of curvature, which has implications for our understanding of the universe's overall geometry.

💡Brilliant.org

Brilliant.org is an educational platform that provides interactive courses in math and science. The video script mentions it as the sponsor and highlights its offerings, which include lessons on astronomy, astrophysics, and other advanced topics that delve deeper into the concepts discussed in the video, such as geodesics and non-Euclidean geometry.

Highlights

We experience three spatial dimensions in everyday life, with a fourth temporal dimension of time necessary to specify events in the universe.

Einstein's general theory of relativity links space and time into a single entity called space-time, where massive objects curve space-time.

The curvature of space-time results in phenomena such as time dilation and the bending of light around massive objects.

Gaussian curvature is a measure of the curvature of a surface, with different properties than common intuition suggests.

A sphere and a saddle shape demonstrate positive and negative Gaussian curvature, respectively, impacting how surfaces can be mapped or wrapped.

The Gaussian curvature of a cylinder, though seemingly curved, is zero, illustrating the complexity of defining curvature on different surfaces.

Gauss's theorema egregium states that Gaussian curvature is preserved under smooth deformation of a surface.

The possibility of determining the Earth's curvature without leaving it is discussed, using precise measurements of circles and their circumferences.

The behavior of parallel lines on curved surfaces, such as converging paths on a sphere, indicates the presence of positive curvature.

The internal angles of triangles on curved surfaces can reveal the nature of the surface's curvature, with angles summing to more or less than 180 degrees.

The universe's large-scale structure is found to be mostly flat, with implications for the sum of internal angles in cosmic triangles.

Geodesics are the shortest paths between points on curved surfaces, differing from the straight lines found in flat spaces.

The metric tensor is introduced as a tool for calculating distances on curved surfaces, extending beyond the Pythagorean theorem.

The metric tensor is essential in Einstein's general theory of relativity, describing the curvature of space-time.

Gravity is reconceptualized in general relativity not as a force, but as a curvature of space-time caused by mass.

Brilliant.org is highlighted as a resource for deeper understanding of the mathematical concepts covered in the video.

The video concludes with a promotion for Brilliant.org, offering a discount for new subscribers interested in exploring the topics further.

Transcripts

Browse More Related Video

Einstein's Field Equations of General Relativity Explained

General Relativity Lecture 4

Tensor Calculus 12: The Metric Tensor in Curved Spaces for Measuring Arc Length

Tensor Calculus 15: Geodesics and Christoffel Symbols (extrinsic geometry)

String theory - Brian Greene

A new way to visualize General Relativity

Related Tags

Space-Time Curvature Einstein Geometry Relativity Astronomy Physics Educational Mathematics Universe