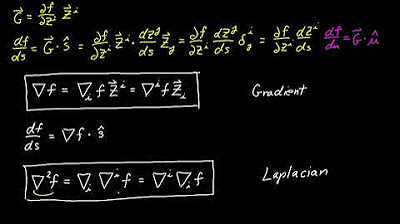Tensor Calculus 13: Gradient vs "d" operator (exterior derivative/differential)
TLDRThis video script delves into the nuances between the gradient operator, often symbolized as del F, and the differential operator, DF. It clarifies the confusion surrounding their nomenclature and explains their technical differences and similarities. The script builds upon the concept of tensor calculus, illustrating how del F represents a vector field pointing towards the steepest increase, while DF is a co-vector field, akin to the level sets of a function. The video further explores the relationship between the two, using the metric and inverse metric tensors to demonstrate the conversion between vector and co-vector fields, ultimately revealing the components of the gradient in various coordinate systems.
Takeaways
- 📚 The video discusses the differences between the gradient operator (del) and the differential operator (D), which are related but distinct in tensor calculus.
- 🔍 The gradient operator, denoted as del F, produces a vector field indicating the direction of steepest increase of a scalar field, while the differential operator, denoted as DF, results in a covector field or one-form.
- 🧭 There is some terminological confusion in the community regarding the names and symbols used for these operators, with different sources using various names like 'exterior derivative' for DF.
- 🔄 The video builds upon concepts from a previous video on raising and lowering tensor indices, suggesting that viewers should watch that for foundational knowledge.
- 🔗 The relationship between del F and DF is established through the action of a covector on a vector, resulting in the directional derivative, which is the same whether computed using del F or DF.
- 📉 The orientation of vectors from del F and covectors from DF point towards the positive values of the scalar field F, indicating a similarity in their directional representation.
- 📚 The video explains that the metric tensor plays a crucial role in converting between the components of a vector and its corresponding covector, and vice versa, using the inverse metric tensor.
- 📏 The components of del F, or the gradient of F, can be derived using the components of DF and the inverse metric tensor, highlighting the connection between the vector and covector fields.
- 🌐 The formula for the gradient in different coordinate systems, such as Cartesian or polar, involves the components of the inverse metric tensor, which accounts for the correct formulation of the gradient.
- 🎼 The video mentions alternative notations for the operations of converting between del F and DF, using musical symbols like flat and sharp, which might be encountered in some texts.
- 📝 The script promises a future video that will delve deeper into the proof of the relationship between del F and DF using tensor products and provide examples in different coordinate systems.
Q & A
What are the two operators discussed in the video that act on functions?
-The two operators discussed are the gradient operator, also known as the del operator, and the D operator.
What is the difference between the gradient of a scalar field and the differential of a scalar field?
-The gradient of a scalar field gives a vector field pointing in the direction of steepest increase, while the differential of a scalar field gives a covector field, also known as a one-form, oriented towards the positive values of the function.
Why is there confusion in the math and physics community regarding the names of the del operator and the D operator?
-There is confusion because some sources use different names for the del operator and the D operator, such as 'gradient of F' for the del operator and 'exterior derivative' or 'differential one-form' for the D operator.
What is the relationship between the gradient operator (del F) and the differential (DF)?
-The gradient operator (del F) and the differential (DF) are related through the concept of directional derivatives. The differential acting on a vector V is equivalent to the gradient of F with a dot product acting on the same vector V.
How does the video explain the connection between the vector space V and the dual space of covector V*?
-The connection is made by taking a vector V in the vector space and pairing it with a covector V dot something in the dual space, which is akin to a dot product with an empty slot waiting to take another vector to produce a scalar.
What is the role of the metric tensor in converting between vector and covector components?
-The metric tensor is used to convert the components of a vector V into the components of a covector V dot something. It helps in changing from the vector components to the covector components and vice versa using the inverse metric tensor.
How does the video relate the concept of raising and lowering tensor indexes to the gradient and differential?
-The video relates the concept by showing that just as a vector V can be paired with a covector V dot something using the metric tensor, the vector field del F can be paired with the covector field DF, which is essentially del F dot something.
What is the significance of the inverse metric tensor in the formula for the gradient of F (del F)?
-The inverse metric tensor components are significant because they allow for the correct formulation of the gradient in non-Cartesian coordinate systems, providing the necessary multiplying terms to ensure the formula is accurate.
How does the video script clarify the use of the metric tensor and its inverse in changing between del F and DF?
-The script provides formulas that show how the metric tensor components are used to convert from the components of the vector field del F to the components of the covector field DF, and how the inverse metric tensor components are used for the reverse process.
What alternative notation does the video mention for switching between del F and DF?
-The video mentions the use of flat and sharp symbols from music as an alternative notation for switching between del F and DF, where the flat operator can change del F into DF and the sharp operator can change DF back into del F.
What coordinate system does the video mention as an example where the inverse metric tensor components affect the gradient formula?
-The video mentions polar coordinates as an example where the inverse metric tensor components introduce an extra term of 1 over R squared in the gradient formula.
Outlines
📚 Understanding the Gradient and D Operator
This paragraph introduces the topic of the video, which is to clarify the differences between the gradient operator (denoted as 'del' or '∇') and the 'D' operator in tensor calculus. The speaker recommends viewers watch a previous video on raising and lowering tensor indexes for foundational knowledge. The paragraph discusses the confusion in terminology within the math and physics community and establishes the definitions used in the video: 'del F' for the gradient and 'DF' for the differential or exterior derivative. It explains that while both operators act on scalar fields, the gradient results in a vector field indicating the direction of steepest ascent, whereas 'DF' results in a covector field, which is related to the level sets of the function. The paragraph concludes by highlighting the similarity in orientation between the vectors and covectors, both pointing towards the positive values of the function.
🔗 The Connection Between del F and DF Through Tensor Indexes
The second paragraph delves into the relationship between the vector space 'V' and the dual space of covectors 'V*', using the metric tensor for the transition between them. It explains how the metric tensor allows the conversion of a vector 'V' into a covector 'V dot something' by using a dot product with an open slot for another vector, resulting in a scalar. The paragraph then draws a parallel between this process and the connection between 'del F' and 'DF', showing that 'DF' acting on a vector 'V' is equivalent to the gradient of 'F' dotted with 'V', thus indicating that 'DF' is essentially 'del F' dotted with a covector. This establishes that 'DF' is the dual covector field of the vector field 'del F', which is referred to as the gradient of 'F' in the video.
📐 Using Metric Tensors to Convert Between Vector and Covector Components
In this paragraph, the speaker reviews the process of using metric tensors to convert between vector and covector components, as previously discussed in a video on raising and lowering tensor indexes. It explains how the dot product 'V dot W' can be computed using the metric tensor components and the components of vectors 'V' and 'W'. The paragraph then demonstrates how to construct a covector 'V dot something' by removing the vector 'W' from the dot product and using the covector bases 'ε^J'. The speaker also introduces the formula for the covector components in terms of the vector components and the metric tensor components. The paragraph concludes by showing that the directional derivative 'DF' can be represented as both 'del F' dotted with a vector 'V' and as a covector formed by 'del F' and the metric tensor, thus confirming the equivalence between 'DF' and 'del F dot something'.
🧩 Deriving the Components of del F Using Inverse Metric Tensors
The final paragraph focuses on deriving the components of 'del F', the gradient of 'F', using the inverse metric tensor. It starts by showing that 'DF', the covector field, can be expanded in the covector basis, with the components being the partial derivatives. The paragraph then establishes that 'DF' is equal to both its expansion in the covector basis and a formula involving the components of 'del F' and the metric tensor components. By equating these two expressions, the paragraph derives a formula that relates the components of 'del F' to the partial derivatives and the components of the inverse metric tensor. The paragraph concludes by discussing how these inverse metric tensor components are essential for obtaining the correct formula for the gradient in various coordinate systems, including Cartesian and polar coordinates, and mentions that the next video will provide a proof and examples of computing 'del F' in different coordinate systems.
Mindmap
Keywords
💡Gradient Operator
💡D Operator
💡Tensor Calculus
💡Scalar Field
💡Vector Field
💡Covector Field
💡Metric Tensor
💡Inverse Metric Tensor
💡Level Sets
💡Directional Derivative
💡Tensor Product
Highlights
The video discusses the differences between the gradient operator (del) and the differential operator (D), which are related but technically different.
Confusion exists in the math and physics community regarding the naming of these operators, with some sources using different terms like 'gradient of F' or 'exterior derivative'.
The gradient of a scalar field (del F) results in a vector field pointing in the direction of steepest increase, while DF gives a covector field or one-form indicating level sets of the function.
Both del F and DF have similar orientations, pointing towards the positive values of the function f, but represent different concepts: a vector field and a covector field, respectively.
A special connection between vector space V and the dual space of covectors V* is made through the dot product with an empty slot, waiting to take another vector to produce a scalar.
The video demonstrates a connection between del F and DF, showing that DF is equal to del F dotted with something, both taking a vector input and producing a scalar.
The concept of raising and lowering tensor indexes is revisited, with the metric tensor facilitating the conversion between vector components and covector components.
The video explains how to compute the dot product using the components of the metric tensor and how to construct a covector using the covector basis.
The directional derivative DF of a scalar field E is shown to be equal to the gradient del F dotted with a vector V, illustrating the relationship between del F and DF.
The video derives a formula for the components of del F using the components of DF and the inverse metric tensor, demonstrating the role of the inverse metric tensor in obtaining the gradient formula.
In Cartesian coordinates, the inverse metric tensor simplifies to the identity matrix, making the components of del F the same as those of DF.
In polar coordinates, the formula for the gradient of F includes additional terms derived from the components of the inverse metric tensor, such as 1/R^2.
The video clarifies that the extra terms in the gradient formula in different coordinate systems come from the components of the inverse metric tensor.
The video mentions an alternative notation using flat and sharp symbols from music to switch between del F and DF, which might be seen in some textbooks or articles.
The next video will cover the proof of why the formula for del F dot something makes sense using tensor products and provide examples of computing del F components in different coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: