2022 AP Physics 1 Free Response #2

Allen Tsao The STEM Coach
14 May 202207:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the gravitational forces acting on two moons, A and B, orbiting a planet with mass M0. The speaker discusses the forces from the planet and between the moons, using Newton's third law. The net gravitational forces on each moon are considered, explaining why one moon's force could be greater. Mathematical expressions for these forces are derived and applied to scenarios where the moons' distances vary. The analysis shows how different positions and distances affect the net forces, providing clear reasoning and justifications for the observed phenomena.

Takeaways
  • 🌑 The scenario involves two identical moons, A and B, orbiting a planet with mass \( m_0 \).
  • 🔗 Each moon has a significant mass, less than the planet's mass \( m_p \).
  • 🌗 The moons' orbits are such that at some point, they align with the planet, causing gravitational interactions.
  • 📐 A free body diagram is used to represent the gravitational forces acting on each moon from the planet and between each other.
  • ⚖️ Newton's third law is mentioned, indicating that the forces between the moons are equal and opposite.
  • 📉 The net gravitational force on each moon is calculated by considering the gravitational pull from the planet and the interaction between the moons.
  • 🌌 The magnitude of the net force on Moon A could be much larger than on Moon B depending on their respective distances from the planet.
  • 📏 The net force on a moon is influenced by the distance between the moon and the planet, with closer distances resulting in stronger gravitational pulls.
  • 🔄 The script discusses conditions under which the net force on one moon could be zero while the other has a non-zero net force.
  • 📘 Derivations are provided for the net force on both moons, considering the gravitational constant \( G \), masses, and distances.
  • 🤔 The script explores different scenarios to justify why the net force on one moon could be larger than the other, considering their positions relative to each other and the planet.
Q & A

  • What are the main forces acting on Moon A?

    -The main forces acting on Moon A are the gravitational force from the planet and the gravitational force from Moon B.

  • Why are the forces between the two moons considered equal and opposite?

    -According to Newton's third law, the forces between two interacting bodies are equal in magnitude and opposite in direction. Therefore, the force Moon A exerts on Moon B is equal and opposite to the force Moon B exerts on Moon A.

  • How can the net gravitational force on Moon A be zero?

    -The net gravitational force on Moon A can be zero if the gravitational force exerted by the planet on Moon A is balanced by the gravitational force exerted by Moon B on Moon A.

  • Under what conditions would the net gravitational force on Moon B be zero?

    -The net gravitational force on Moon B would be zero if the gravitational force exerted by the planet on Moon B is equal and opposite to the gravitational force exerted by Moon A on Moon B.

  • What happens to the net force on Moon A if the distance between the planet and Moon B (rB) is much smaller than the distance between the planet and Moon A (rA)?

    -If rB is much smaller than rA, the gravitational force exerted by the planet on Moon B will be much larger compared to the gravitational force exerted by the planet on Moon A, making the net force on Moon A much smaller.

  • Why would the net force on Moon B be larger than the net force on Moon A in certain conditions?

    -The net force on Moon B could be larger than the net force on Moon A if the distance between the planet and Moon B (rB) is much smaller than the distance between the planet and Moon A (rA), resulting in a stronger gravitational pull on Moon B.

  • How do you calculate the gravitational force between the planet and Moon A?

    -The gravitational force between the planet and Moon A is calculated using the formula: F = G * (m_planet * m_moonA) / rA^2, where G is the gravitational constant, m_planet is the mass of the planet, m_moonA is the mass of Moon A, and rA is the distance between the planet and Moon A.

  • What is the significance of the distance rA - rB in the context of the forces between the moons?

    -The distance rA - rB represents the distance between Moon A and Moon B. It is used to calculate the gravitational force between the two moons.

  • What could cause the net force on Moon A to be non-zero while the net force on Moon B is zero?

    -The net force on Moon A could be non-zero if the gravitational force exerted by the planet on Moon A and the gravitational force exerted by Moon B on Moon A do not cancel out. This situation can arise if the distance and masses involved result in an imbalance of forces.

  • How do the derived expressions for net forces support the reasoning about the relative magnitudes of forces on the moons?

    -The derived expressions for net forces show that the net force on Moon B is dependent on the gravitational pull from the planet and the opposing force from Moon A. When rB is much smaller than rA, the force from the planet on Moon B is significantly larger, supporting the reasoning that the net force on Moon B could be greater than the net force on Moon A.

Outlines
00:00
🌌 Gravitational Forces on Moons in Orbit

The paragraph discusses a scenario where two identical moons, A and B, orbit a planet with mass m0. Both moons have a significant mass, less than the planet's mass mp. The gravitational forces acting on each moon are detailed, including the forces from the planet (Fa_planet and Fb_planet) and the force between the moons (Fab). The net gravitational force on each moon is explored, with an explanation of how it could vary depending on the distances (ra and rb) from the planet. The paragraph also delves into the conditions under which the net force on one moon could be much larger than the other, emphasizing the importance of the relative distances and the alignment of the forces.

05:01
📚 Analyzing Net Gravitational Force Equations

This paragraph continues the discussion on the gravitational forces between the planet and the two moons, focusing on the mathematical expressions that describe the net force on each moon. It presents the equations for calculating the net force on moon A (F_net_A) and moon B (F_net_B), considering the gravitational constant (g), the masses of the planet and moons, and the distances between them. The paragraph also examines specific conditions that would result in one moon experiencing a significantly larger net force than the other, such as when the distance between the moons (rb) is much smaller than the distance from the planet to moon A (ra). The summary underscores the importance of these equations in understanding the dynamics of the celestial bodies in question.

Mindmap
Keywords
💡Ionic
The term 'ionic' in the context of the video script refers to the state of the moons, suggesting they are charged particles. However, it seems to be a misinterpretation or misreading, as the script might be referring to 'identical' moons, which would mean the moons are similar in size, mass, and other physical properties. The term is used early in the script to describe the moons orbiting the planet.
💡Orbit
Orbit is the curved path of one object around another due to gravity. In the video, the term is used to describe the motion of two moons (A and B) around a planet with mass 'm0'. The concept of orbit is central to understanding the dynamics and forces at play in the scenario presented.
💡Mass
Mass is a measure of the amount of matter in an object, and it plays a crucial role in gravitational interactions. In the script, 'm0' represents the mass of the planet, while the masses of the moons are described as 'significant but less than mp'. The mass of the objects influences the gravitational forces between them.
💡Gravitational Forces
Gravitational forces are the attractive forces between two masses. The script discusses how each moon experiences gravitational forces from the planet and from the other moon, represented by 'fab' and 'f_planet_on_a/b'. These forces are essential in analyzing the net force acting on each moon.
💡Newton's Third Law
Newton's Third Law states that for every action, there is an equal and opposite reaction. In the script, it is mentioned to justify that the forces 'fab' experienced by both moons are equal and opposite, which is a fundamental concept in understanding the balance of forces in the system.
💡Net Gravitational Force
The net gravitational force is the vector sum of all gravitational forces acting on an object. The script discusses calculating the net force on each moon by considering the gravitational pull from the planet and the interaction between the moons. Understanding the net force is key to analyzing the motion and stability of the moons' orbits.
💡Free Body Diagram
A free body diagram is a simplified representation used to visualize all the forces acting on a body in a system. The script instructs to draw such a diagram for Moon A, showing the forces from the planet and Moon B, which helps in visualizing and calculating the net force on the moon.
💡Distance
Distance is a measure of the interval between two points, and in the context of the script, it refers to the separation between the moons and the planet. The distances 'ra' and 'rb' are crucial in calculating the gravitational forces using the inverse-square law.
💡Inverse-Square Law
The inverse-square law relates the strength of a physical quantity to the inverse of the square of the distance from the source. In the script, this law is implicitly used to calculate the gravitational forces between the planet and the moons, as well as between the moons themselves, with the formula involving mass and the square of the distance.
💡Net Force
Net force is the vector sum of all the forces acting on an object. The script discusses the net force on each moon, 'f_net_a' and 'f_net_b', which is determined by the gravitational forces and their directions. The comparison of net forces on the moons is central to the discussion in the video.
💡Equilibrium
Equilibrium in physics refers to a state where the net force on an object is zero, meaning it is not accelerating. The script explores a scenario where the net force on Moon B could be zero if the forces from the planet and Moon A cancel each other out, illustrating a state of equilibrium.
Highlights

Two identical moons, A and B, orbit a planet with mass m0.

The mass of each moon is significant but less than the mass of the planet, mp.

The moons' orbits and the planet's tumors are aligned as depicted in the figure.

A free body diagram is drawn to represent the gravitational forces acting on Moon A and Moon B.

Force from the planet on Moon A is labeled as F_pa, and the force from Moon B on Moon A as F_ab.

According to Newton's third law, the forces F_ab and F_ba are equal and opposite.

The net gravitational force on each moon is considered, with the magnitude potentially differing.

The net force on Moon A could be much larger than on Moon B depending on their distances from the planet.

If the distance rb is very small compared to ra, the gravitational pull from the planet on Moon B is significantly larger.

The net force on Moon B would be larger if Moon A and B are close together.

The net force on Moon A could be greater than zero if the forces F_ab and F_planet_on_b cancel each other out.

Expressions for the net force on Moon A and Moon B are derived using gravitational force equations.

The net force on Moon A is the sum of the gravitational forces from the planet and Moon B.

The net force on Moon B is calculated by subtracting the force from Moon A from the planet's gravitational pull.

The expressions support the reasoning that the net forces on the moons can differ significantly.

If the distance rb is much smaller than ra, the net force on Moon B could be significantly larger than on Moon A.

The gravitational forces and their effects are dependent on the relative positions and distances of the moons and the planet.

Transcripts

Browse More Related Video

AP Physics Workbook 3.N Newton's Law of Universal Gravitation

AP Physics 1 Dynamics Review

Newton's Laws of Motion and Forces

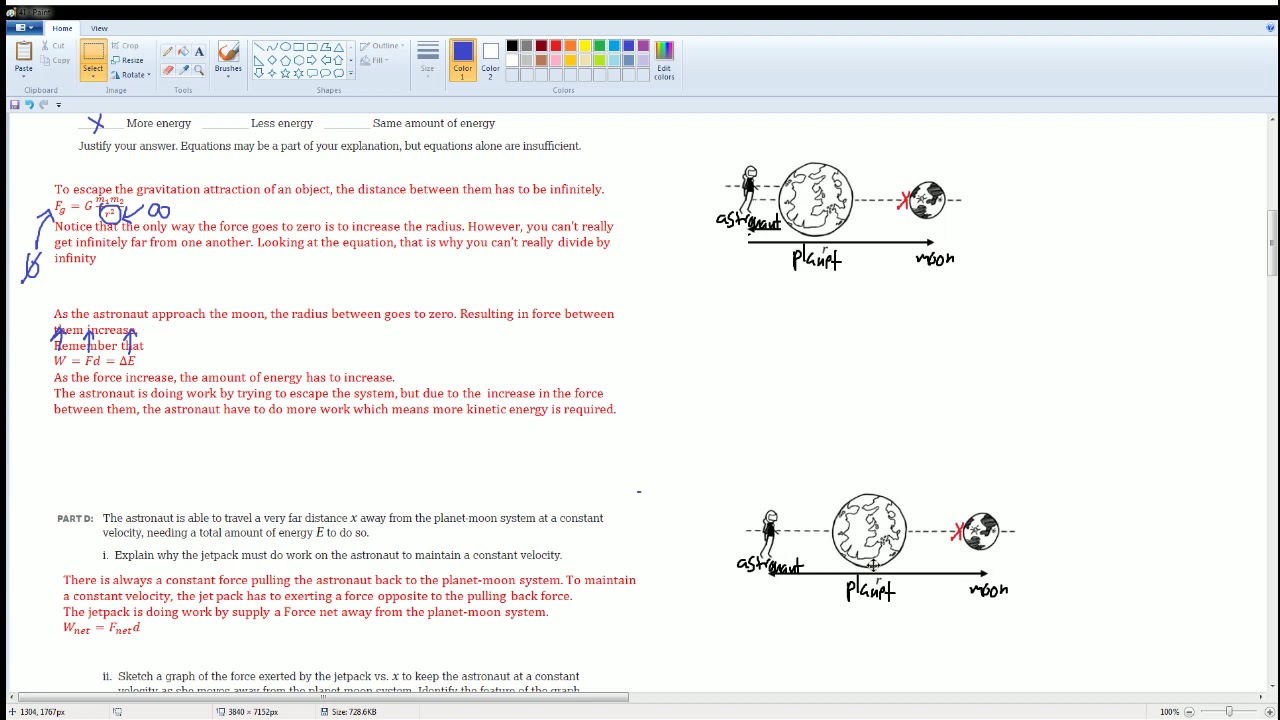
AP Physics Workbook 4.I Gravitational Potential Energy

Force | Free Body Diagrams | Physics | Don't Memorise

Centripetal Acceleration & Force - Circular Motion, Banked Curves, Static Friction, Physics Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Gravitational ForcesOrbital MechanicsCelestial BodiesPhysics AnalysisNewton's LawsMoons OrbitPlanetary MassNet ForceSpace DynamicsAstronomical Events