AP Calculus AB Unit 2 Review | Derivatives
TLDRThis video tutorial covers Unit 2 of Calculus AB, focusing on the concept of derivatives as the rate of change or slope of a function at a specific point. It explains the difference between average and instantaneous rates of change, introduces various notations for derivatives, and highlights the importance of continuity for differentiability. The lesson delves into differentiation rules, including the power rule and trigonometric functions, and demonstrates how to find the equation of a tangent or normal line. The instructor encourages practice and offers help for any confusing topics, emphasizing the necessity of mastering differentiation in calculus.
Takeaways
- 📚 Derivatives are essential to learning Calculus, representing the rate of change or the slope of a function at a specific point, also known as the instantaneous rate of change.
- 🔍 To find the average rate of change, you calculate the slope between two points on the graph, which is different from the instantaneous rate of change.
- 📈 Derivatives can be expressed in various notations, all of which mean the same thing, such as f'(x), df/dx, and lim(h→0) [f(x+h) - f(x)] / h.
- 📉 Continuity is a prerequisite for differentiability, but not all continuous functions are differentiable; the derivative must be the same when approaching a point from both sides.
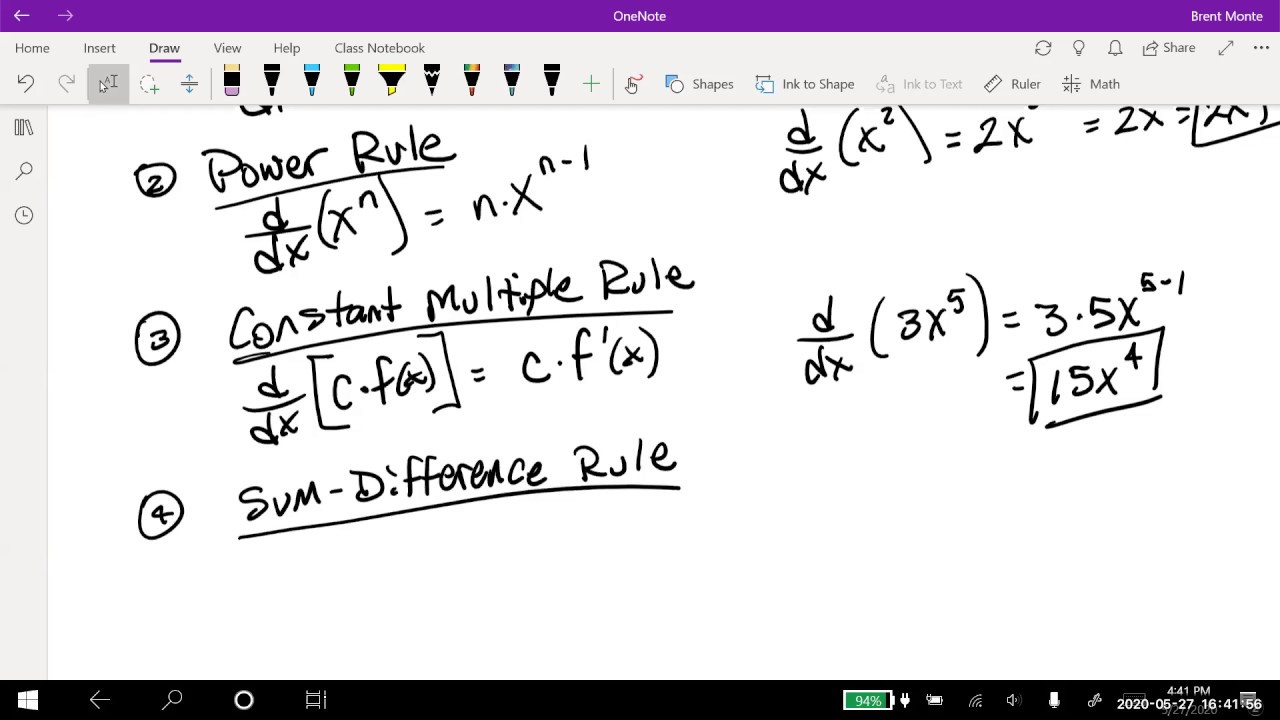
- 🔑 The power rule is a fundamental differentiation rule, allowing you to find the derivative of a function like x^n by multiplying by n and reducing the power by one.
- ➕➖ When differentiating terms with addition and subtraction, you can differentiate each term separately.
- 🔄 The product and quotient rules are essential for differentiating functions involving multiplication and division, with specific formulas to apply.
- 📊 Trigonometric functions have their own set of differentiation rules, with patterns such as the derivative of sine being cosine, and vice versa.
- 📐 The equation of a tangent line can be found using the point-slope formula, where the slope is the derivative at a given point.
- ⏏️ To find the equation of a normal line, which is perpendicular to the tangent, use the negative reciprocal of the slope.
- 🎓 Mastery of differentiation rules is crucial, and with practice, they become more intuitive and even enjoyable.
Q & A
What is the primary focus of Unit 2 in the 'Calc AB' course?
-Unit 2 of 'Calc AB' focuses on various methods to find the derivative and important rules that students must know for differentiation, which is essential to learning Calculus.
Why is it important to watch the Unit 1 video before Unit 2?
-The Unit 1 video likely covers foundational concepts that are prerequisites for understanding the derivative and differentiation rules discussed in Unit 2.
What is the definition of a derivative in the context of this script?
-A derivative is the rate of change of a function, representing the slope of the function at a specific point, also known as the instantaneous rate of change or the slope of the tangent line.
How is the average rate of change different from the instantaneous rate of change?
-The average rate of change refers to the slope between two points on a graph, while the instantaneous rate of change refers to the slope at a single point, represented by the derivative.
What is the formula used to estimate the derivative at a point using two points around it?
-The formula used to estimate the derivative is the slope formula: (f(B) - f(A)) / (B - A).
How can you express the derivative using limits?
-The derivative can be expressed using limits in different forms, such as returning the derivative as a function or returning the derivative at a specific point.
What are the common notations used to represent the derivative?
-Common notations for the derivative include f'(x), df/dx, and d/dx f(x), all of which mean the same thing.
Why is continuity a requirement for differentiability, but not all continuous functions are differentiable?
-Continuity is a prerequisite for differentiability because a function must be defined at every point to have a derivative. However, some functions, like those with sharp turns or breaks, are continuous but not differentiable at certain points due to the absence of a well-defined slope.
What is the power rule for differentiation, and how is it applied?
-The power rule states that the derivative of x to the power of n is n times x to the power of (n-1). It is applied by multiplying the exponent by the original function and then reducing the exponent by one.
How do you differentiate a function that is a product or quotient of two functions?
-For a product, you use the product rule: f'(x)g(x) + g'(x)f(x). For a quotient, you use the quotient rule, which involves subtracting the derivative of the denominator times the original numerator from the original denominator squared.
What are the basic trigonometric differentiation rules mentioned in the script?
-The basic trigonometric differentiation rules include the derivative of sine being cosine, the derivative of tangent being secant squared, and the derivatives of cosecant, secant, and cotangent involving negative secant and tangent terms.
How do you find the equation of a tangent line to a curve at a given point?
-To find the equation of a tangent line, you use the point-slope formula with the point on the curve and the derivative (slope) at that point.
What is the relationship between the slope of a tangent line and the normal line at a point on a curve?
-The slope of the normal line to a curve at a point is the negative reciprocal of the slope of the tangent line at that point.
Outlines
📚 Introduction to Derivatives and Differentiation Basics
This paragraph introduces Unit 2 of Calculus AB, focusing on the concept of derivatives as the rate of change of a function, which is essentially the slope at a particular point, also known as the instantaneous rate of change. The paragraph explains the difference between the average rate of change, which involves the secant line, and the instantaneous rate of change, which is associated with the tangent line. It also covers the importance of understanding different notations for derivatives, the relationship between continuity and differentiability, and the conditions under which a function may not be differentiable, such as at points of sharp turns. The paragraph sets the stage for the differentiation rules that will be discussed in the subsequent content.
🔍 Derivation Rules and Application in Calculus
This paragraph delves into the various rules of differentiation, starting with the basic rules such as the derivative of a constant being zero and the power rule for functions like x to the power of 5. It then explains the product and quotient rules for differentiating expressions involving multiplication and division. The paragraph also touches on trigonometric differentiation rules, which require memorization but can be simplified by recognizing patterns among the derivatives of sine, cosine, tangent, cotangent, secant, and cosecant functions. The summary includes examples of how to apply these rules to find derivatives of functions like x cubed and x squared times ln(x). Additionally, the paragraph discusses the process of finding the equation of a tangent line using the point-slope formula and the normal line by taking the negative reciprocal of the slope. The summary concludes with an encouragement to practice these differentiation rules until they become second nature and offers assistance for any confusion, inviting viewers to subscribe for updates on future unit reviews.
Mindmap
Keywords
💡Derivative
💡Instantaneous Rate of Change
💡Average Rate of Change
💡Continuity
💡Differentiability
💡Power Rule
💡Product Rule
💡Quotient Rule
💡Trigonometric Functions
💡Tangent Line
💡Normal Line
Highlights
Introduction to Unit 2 of Calculus, focusing on differentiation methods and essential rules.
Differentiation is essential to learning Calculus, emphasizing the importance of understanding derivatives.
Derivative defined as the rate of change of a function, representing the slope at a specific point.
Differentiation between the instantaneous rate of change and the average rate of change.
Explanation of how to estimate the derivative at a point using surrounding points.
Introduction to various notations used to express derivatives.
The relationship between continuity and differentiability, with examples of functions that are continuous but not differentiable.
Differentiation rules overview, including constant, power, product, and quotient rules.
Trigonometric differentiation rules and their memorization techniques.
Demonstration of how to find the equation of a tangent line using the derivative.
Method to find the equation of a normal line by using the negative reciprocal of the slope.
Emphasis on the necessity of differentiation in calculus and the importance of practicing the rules.
Encouragement for viewers to comment if they are confused and a promise to assist with any topic.
Invitation to subscribe to the channel for updates on future unit reviews.
A reminder that differentiation should start to come naturally with practice and can be enjoyable.
Conclusion of the video with a summary of the importance of understanding differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: