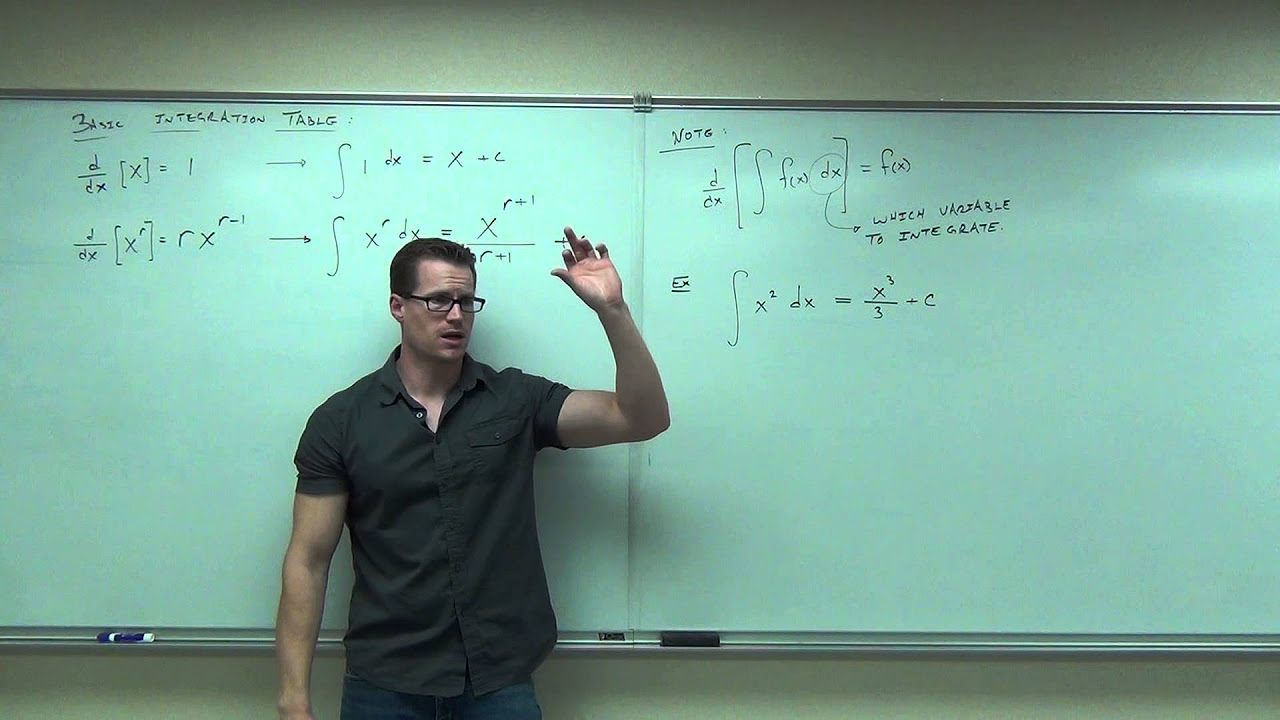Calculus 1 Lecture 4.3: Area Under a Curve, Limit Approach, Riemann Sums
TLDRThe video script is an educational lesson on calculus, focusing on the concept of finding areas under a curve by summing up rectangles. It introduces the idea of anti-derivatives, integration by substitution, and the sigma notation for summation. The instructor explains the properties of summation, provides formulas for common sums, and demonstrates how to apply these concepts to find the area under a curve using the rectangular method. The lesson also covers the concept of net signed area and illustrates the process with step-by-step examples, emphasizing the importance of practice and understanding the mathematical principles involved.
Takeaways
- 📚 The lesson focuses on understanding the concept of anti-derivatives and integration by substitution, emphasizing the importance of knowing why these mathematical processes work, not just how to apply them.
- 📈 The instructor introduces the idea of finding the area under a curve using integration, explaining that the integral is essentially the limit of a sum, which represents the area when the number of rectangles approaches infinity.
- 🎓 Sigma notation is explained as a method of representing summation, with properties that allow for manipulation similar to those of derivatives and integrals, such as factoring out constants and separating sums.
- 🔢 Common summation formulas are provided for quickly calculating the sum of sequences like 1+2+3+...+n, which are useful in various mathematical applications, including integration.
- 📉 The concept of 'net signed area' is discussed, which accounts for areas above and below the x-axis, with the total area calculated as the positive areas minus the negative areas.
- 📝 The process of finding the area under a curve involves breaking the area into rectangles, finding the height of each rectangle using the function at an arbitrary point, and then summing these areas using a limit as the number of rectangles approaches infinity.
- 📌 The importance of practice is highlighted, with the instructor emphasizing that skipping homework can lead to a lack of preparedness for tests, as test questions often relate directly to the homework problems.
- 📉 The method for finding the area under a curve is demonstrated step by step, including calculating the width of each rectangle (Delta X), determining the arbitrary point within each interval (XK dot), and finding the function's value at that point (F of XK dot).
- 📚 The instructor provides a detailed example of finding the area under the curve of a quadratic function, showing the algebraic manipulations and the application of limits to find the exact area.
- 🔑 Key formulas and properties for summation and integration are reiterated, such as the ability to factor out constants and the formulas for the sum of the first n integers and the sum of the squares of the first n integers.
- 📈 The lesson concludes with a reminder of the importance of understanding the underlying concepts of calculus, such as limits and the process of integration, rather than just memorizing formulas and procedures.
Q & A
What is the purpose of Sigma notation in calculus?
-Sigma notation is used to represent the sum of a sequence of terms. It is a shorthand way to write the sum of a series of numbers or expressions, often used in calculus to represent the addition of a function evaluated at different points, such as when finding areas under a curve using the rectangular method.
What does the property of pulling out a constant from a summation mean?
-The property states that if you have a summation of a function of K times a constant, and the constant does not depend on K, you can factor the constant out in front of the summation sign. This simplifies the expression and makes it easier to evaluate the sum.
Can you explain the concept of 'area as a limit' in the context of calculus?
-The concept of 'area as a limit' refers to finding the area under a curve by dividing the region into an infinite number of infinitesimally small rectangles and summing their areas. As the number of rectangles approaches infinity, the width of each rectangle approaches zero, and the sum of their areas approaches the actual area under the curve, which is the limit of this process.
What are the steps involved in finding the area under a curve using the rectangular method?
-The steps are: 1) Determine the width of each rectangle (ΔX), 2) Find the height of each rectangle by evaluating the function at an arbitrary point within each interval, 3) Multiply the width by the height to find the area of each rectangle, 4) Sum the areas of all rectangles, and 5) Take the limit as the number of rectangles approaches infinity to find the exact area.
What is the difference between the anti-derivative method and the rectangular method for finding areas under a curve?
-The anti-derivative method involves finding the antiderivative of the function and then applying the fundamental theorem of calculus to find the area between two points. The rectangular method, on the other hand, involves approximating the area under the curve by summing the areas of rectangles that fit under the curve, and then taking the limit as the number of rectangles approaches infinity.
What is the formula for the sum of the first n natural numbers?
-The formula for the sum of the first n natural numbers is n * (n + 1) / 2. This formula is derived from the closed form of the summation of K from 1 to n.
How do you find the sum of a series of numbers each raised to a power, such as the sum of the first n squares?
-For the sum of the first n squares, the formula is n * (n + 1) * (2n + 1) / 6. This is derived from the closed form of the summation of K^2 from 1 to n.
What does it mean to take the limit as n approaches infinity in the context of finding areas under a curve?
-Taking the limit as n approaches infinity means that you are increasing the number of rectangles to an infinite amount, which makes the width of each rectangle approach zero. This process refines the approximation of the area under the curve to an exact value by eliminating any error due to the finite number of rectangles.
What is the significance of choosing left, right, or midpoints when dividing the interval for the rectangular method?
-Choosing left, right, or midpoints determines where on the interval the height of each rectangle is measured. This choice can affect the accuracy of the approximation, as different choices may lead to different sums. However, in the limit as n approaches infinity, all three methods yield the same exact area under the curve.
Why is it important to understand the properties of summations when working with Sigma notation?
-Understanding the properties of summations allows you to manipulate and simplify expressions involving Sigma notation more effectively. This is crucial for solving problems in calculus, such as finding areas under a curve, where you often need to sum a series of terms.
Outlines
📚 Mastering Anti-Derivatives and Integration by Substitution
The paragraph introduces the concept of anti-derivatives, explaining how they are used to 'undo' derivatives, and mentions the integration by substitution as a method of finding anti-derivatives. The speaker also discusses the importance of understanding why these mathematical processes work and introduces the topic of area calculation as a limit, which is a fundamental concept in calculus. Sigma notation is introduced as a method of representing summation, with an example provided to illustrate its use.
🔢 Sigma Notation and Its Properties
This section delves deeper into sigma notation, explaining its significance in summing sequences and its properties. The properties discussed include factoring out constants and the ability to split sums involving addition and subtraction. The speaker provides examples to clarify these properties and ensures that the audience is comfortable with the concepts before proceeding.
📐 Understanding Summation Formulas and Calculating Areas
The speaker discusses various formulas for summation, which are essential for calculating the areas under a curve. These include formulas for the sum of the first n natural numbers, the sum of their squares, and the sum of their cubes. The importance of these formulas in simplifying the process of finding areas is emphasized, and the speaker ensures that the audience is familiar with these concepts.
📉 The Concept of Net Signed Area in Calculus
This part of the script introduces the concept of net signed area, which takes into account the positive and negative areas under a curve. The explanation clarifies that the area above the x-axis is considered positive, while the area below is negative. The process of calculating the total area by finding the difference between positive and negative areas is discussed, providing a deeper understanding of how areas under a curve are calculated in calculus.
📝 Steps for Calculating Areas Under a Curve
The speaker outlines the steps involved in calculating the area under a curve using limits and summation. This includes finding the width of rectangles (Delta X), determining the height of these rectangles using an arbitrary point (XK dot), and then applying the function to find the area of each rectangle. The process is explained in detail, with an emphasis on the importance of each step in arriving at the correct area calculation.
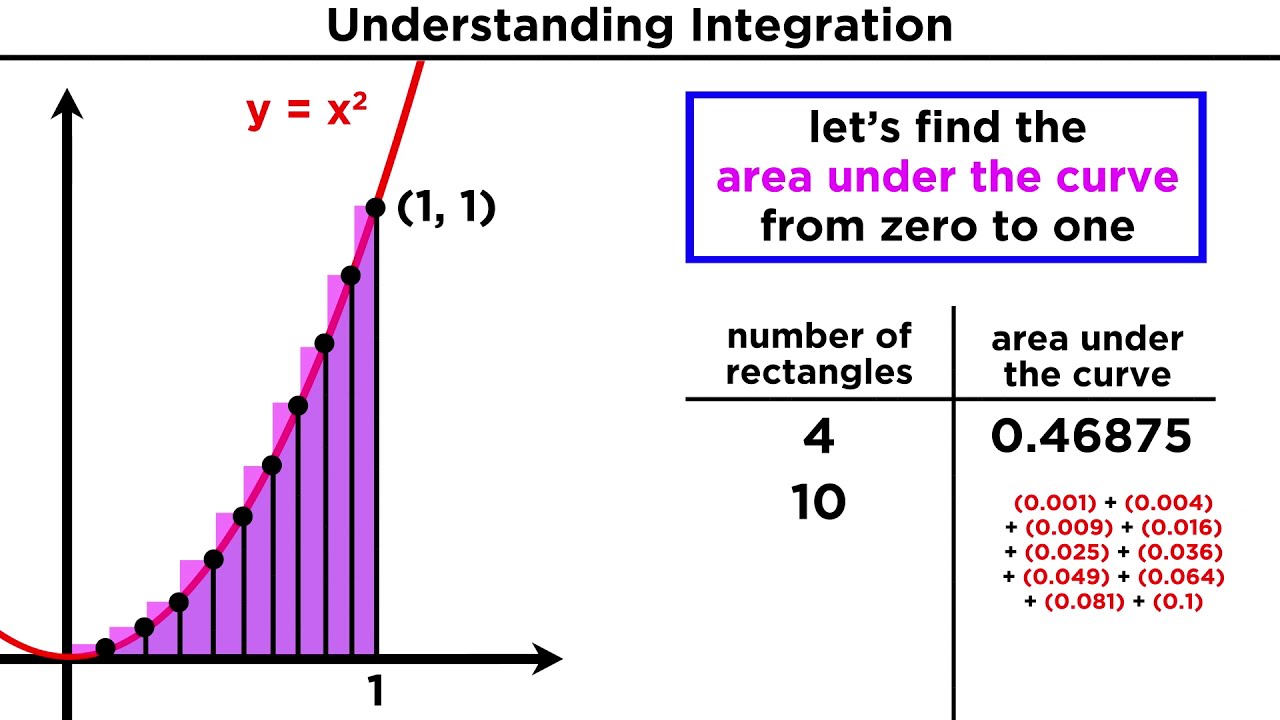
📈 Applying the Steps to Find the Area Under a Specific Function
The paragraph demonstrates the application of the previously discussed steps to find the area under the function f(x) = x^2 between 0 and 1. The process involves calculating Delta X, determining the right endpoints (XK dot), finding the function's value at these points, and then setting up the summation with the appropriate expressions. The speaker guides the audience through each step, ensuring they understand how to apply the formulas and concepts to find the area.
🔍 Detailed Explanation of the Area Calculation Process
This section provides a detailed explanation of the process of calculating the area under a curve, focusing on the algebraic manipulation of the summation expression. The speaker simplifies the expression by factoring out constants and separating the summation into manageable parts. The importance of correctly applying algebraic techniques to simplify the expression before taking the limit as n approaches infinity is emphasized.
🎯 Final Steps in Calculating the Exact Area Using Limits
The speaker concludes the area calculation by taking the limit as n approaches infinity, which transforms the approximation into an exact value. The process involves simplifying the expression and applying the limit to each term, resulting in the final area. The explanation highlights the importance of careful algebraic manipulation and understanding the concept of limits in calculus.
📚 Recap and Further Exploration of Net Signed Area
The speaker recaps the concept of net signed area and its significance in calculus. They also express a desire to further explore the topic and explain the difference between net signed area and total area. The audience is encouraged to understand the implications of calculating areas above and below the x-axis and how these contribute to the overall area under a curve.
📉 Illustration of Net Signed Area with an Example
This paragraph provides an example to illustrate the concept of net signed area, using a function that dips below the x-axis. The speaker demonstrates how to calculate the area using left endpoints and emphasizes the importance of understanding the process. The example serves to clarify the concept of net signed area and its application in calculus.
🔢 Detailed Algebraic Manipulation in Area Calculation
The speaker guides the audience through the algebraic manipulation of the summation expression obtained from the area calculation. The focus is on correctly distributing, simplifying, and combining terms to prepare for the application of the limit. The explanation highlights the importance of precise algebraic work in arriving at the correct area under a curve.
🏁 Conclusion of Area Calculation and Emphasis on Practice
The paragraph concludes the area calculation by taking the limit as n approaches infinity, resulting in the final area. The speaker emphasizes the importance of practice, explaining how skipping homework can negatively impact test performance. The audience is encouraged to practice the steps and concepts covered in the lesson to ensure understanding and proficiency.
Mindmap
Keywords
💡Anti-derivative
💡Integration by substitution
💡Sigma notation
💡Limit
💡Area under a curve
💡Rectangular method
💡Arbitrary point
💡Net signed area
💡Summation properties
💡Definite integral
Highlights
Introduction to anti-derivatives and the concept of reversing derivatives to find integrals.
Explanation of integration by substitution as a method of finding anti-derivatives.
Section 4.3 focuses on understanding the concept of area in calculus and its relation to integrals.
Discussion of Sigma notation, its meaning, and its use in summation.
Properties of summation that allow manipulation similar to derivatives and integrals.
Illustration of how to factor out constants from a summation.
Clarification on the limitations of distributing variables within summation notation.
Presentation of common summation formulas and their applications.
Understanding the concept of area as a limit and its significance in calculus.
Introduction to rectangular methods for approximating areas under a curve.
Explanation of how to find the width of each subinterval for rectangular approximations.
The process of selecting arbitrary points within each subinterval to determine rectangle heights.
Building rectangles to approximate the area under a curve and the concept of refining the approximation.
Transitioning from approximation to exact area calculation using limits.
The integral as a representation of the limit of a sum, and its connection to the area under a curve.
Practical steps for calculating definite integrals and their geometric interpretation.
The choice of arbitrary points (left, right, or midpoint) in the rectangular method and its impact on calculations.
Detailed example demonstrating the calculation of area under a curve using the rectangular method and limits.
The concept of net signed area versus total area in calculus and its implications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: