Integration by parts
TLDRIn this engaging video, Sara from Starfish Maths dives into the concept of integration by parts, a technique she's particularly fond of. She begins by presenting the formula and explaining its components, using the terms 'u' and 'v' to represent the integral and its derivative, respectively. Sara then guides viewers through six examples, four of which are indefinite integrations and two are definite integrations with limits. These examples include challenging scenarios involving logarithmic and trigonometric functions, as well as exam-style questions to test understanding. Throughout the video, she emphasizes the importance of choosing the right 'u' and 'v' for the integration by parts formula and demonstrates how to apply it iteratively when necessary. Sara also shares a clever trick for integrating the natural logarithm function, which doesn't have a straightforward integral. The video concludes with an encouragement to practice and offers resources for further learning, including online tuition through her website and email.
Takeaways
- 📚 Start with the formula for integration by parts and understand it well, as it is fundamental to solving the problems.
- 🔍 Identify 'u' and 'v' in the given integral where 'u' is what you can easily differentiate and 'v' is what remains after differentiation.
- ✅ Practice differentiating and integrating out terms to become familiar with the process.
- 🔁 Remember that you can apply integration by parts more than once if necessary, although typically up to two times is sufficient.
- 📉 Look for terms that simplify upon differentiation, such as '3x' which simplifies to '3', making the remaining integral easier.
- 🧮 Use the formula u \cdot v - \int v \cdot u' \, dx to structure your solution.
- 📈 In the case of trigonometric functions, differentiate the term that will alternate between sine and cosine upon differentiation to simplify the integral.
- 📌 When faced with a logarithmic function, use a clever trick by differentiating it and treating the constant multiplier as 'v'.
- 📐 For definite integration, apply the limits to 'u' and 'v' accordingly and simplify the expression step by step.
- 📝 Keep track of the signs, especially when dealing with trigonometric functions and their derivatives.
- 🧠 Practice is key; work through various examples to solidify your understanding and improve your problem-solving skills.
- 📧 For more information on online tuition or to get in touch, visit the website starfishmaths.com or email starfishmaths@gmail.com.
Q & A
What is the formula for integration by parts?
-The formula for integration by parts is given by ∫u dv = uv - ∫v du, where u and v are functions that you choose to integrate by parts.
Why would you choose to use integration by parts?
-You would choose to use integration by parts when you have a product of two functions, one of which can be easily differentiated, and the other is more difficult to integrate directly.
How do you decide which function to treat as u and which as v in integration by parts?
-You typically choose the function that simplifies easily upon differentiation as u, and the one that remains complex as v. The goal is to make the subsequent integral easier to solve.
What is the first step in applying integration by parts to an integral?
-The first step is to choose the functions u and v such that u is the function that simplifies upon differentiation and v is the function that does not.
What does the dash in the script represent?
-The dash in the script represents the derivative of the function that follows it, such as u' or v'.
How many examples of integration by parts does the video provide?
-The video provides six examples of integration by parts, four of which are indefinite integration and two are definite integration using limits.
What is the purpose of the examples in the video?
-The purpose of the examples is to demonstrate how to apply the integration by parts formula to different types of integrals, including those that are more complex or do not yield to simpler integration techniques.
What is the significance of the term 'indefinite integration' in the context of the video?
-Indefinite integration refers to the process of finding the antiderivative of a function without specific limits, resulting in an answer that includes a constant of integration, typically denoted by 'C'.
How does the video handle the integration of logarithmic functions?
-The video demonstrates a clever trick for integrating logarithmic functions by using integration by parts to transform the integral into a more manageable form.
null
-null
What is the general approach when applying integration by parts more than once?
-When applying integration by parts multiple times, you would typically choose a new u and v for each subsequent application, ensuring that the new u simplifies upon differentiation.
How does the video handle definite integration with limits?
-The video demonstrates how to apply the integration by parts formula within definite integrals by including the limits of integration in the formula and simplifying the result accordingly.
What is the importance of practicing integration by parts?
-Practicing integration by parts helps to solidify understanding of the technique and prepares you for more complex integrals that may appear in exams or real-world applications.
Outlines
📚 Introduction to Integration by Parts
In the first paragraph, Sara introduces the topic of integration by parts, expressing her enthusiasm for the method. She explains that the video will cover the integration by parts formula, provide a walkthrough, and include six examples. Four of these examples will be indefinite integrations, and two will be definite integrations with limits. The examples also include exam-style questions. Sara encourages viewers to participate by pausing the video to work through the problems at their own pace. She emphasizes the importance of recognizing when to apply the integration by parts formula, which involves identifying one function that is easily differentiated (u) and another that is not (v), and then applying the formula: ∫u dv = uv - ∫v du. The paragraph concludes with the setup for the first example, which involves integrating 6x^2 * ln(x).
🔍 Choosing U and V for Integration by Parts
The second paragraph delves into the process of selecting the correct functions for u and v when applying integration by parts. Sara illustrates this with an example involving the product of 3x and e^(-x). She explains that the goal is to simplify the integral by differentiating a term that, when integrated, leaves behind a simpler expression. In this case, differentiating 3x simplifies the integral significantly. Sara then demonstrates the integration by parts formula, showing how to handle the integral of the product of these functions. She also touches on the importance of correctly handling the signs and the process of integrating e^x and its derivative. The paragraph concludes with a brief mention of her other videos that cover differentiation and integration of exponential functions.
🧮 Applying Integration by Parts to Trigonometric Functions
The third paragraph focuses on the application of integration by parts to trigonometric functions. Sara discusses the challenges of integrating products involving x^2 and sin(x), noting that differentiating x^2 repeatedly only alternates between sine and cosine, which doesn't simplify the integral significantly. She decides to differentiate x^2 and integrate sin(x), applying the integration by parts formula. The paragraph also includes a nested application of integration by parts to the resulting integral, which simplifies the problem further. Sara emphasizes the iterative nature of the process and the need to apply integration by parts more than once in complex cases. The paragraph concludes with a direct integration of the simplified expression, resulting in an answer involving a constant of integration.
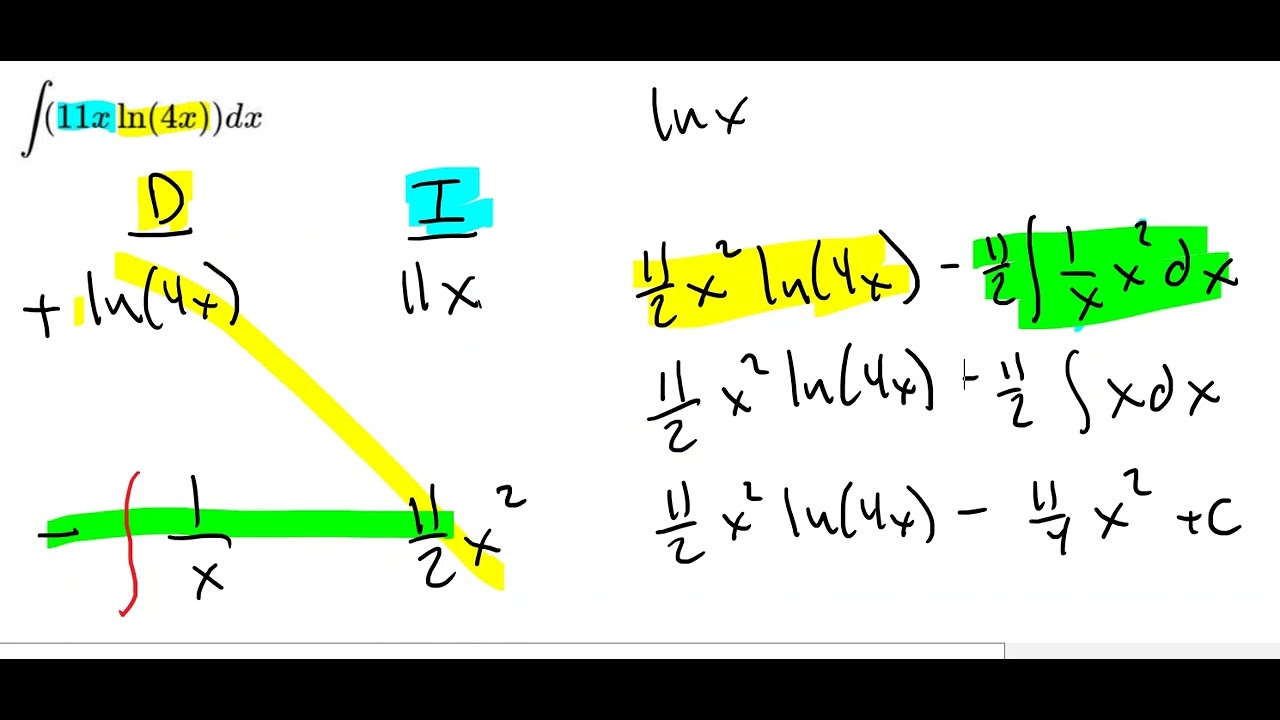
📏 Integration by Parts with Logarithmic Functions
In the fourth paragraph, Sara demonstrates a clever trick for integrating logarithmic functions using integration by parts. She shows how to integrate ln(x) by introducing a factor of 1 and treating it as v, which simplifies the integration process. The paragraph also covers the use of limits in definite integration by parts, using an example with sin(2x). Sara walks through the process of applying the formula with limits and emphasizes the importance of understanding the limits of integration. The paragraph concludes with a step-by-step solution to the example, which involves evaluating the integral at specific limits and simplifying the final answer to π/4.
🧐 Final Example and Conclusion
The final paragraph presents a challenging example involving the logarithmic function ln(2x) and concludes with a summary of the video's content. Sara encourages viewers to attempt the example on their own before revealing the solution. She demonstrates the process of differentiating ln(2x) and integrating 1/x, applying the integration by parts formula and including the limits of integration. The paragraph concludes with a reminder for viewers to practice with various examples and to reach out for more information on online tuition through her website or email. Sara thanks the viewers for watching and encourages them to continue learning and having fun with mathematics.
Mindmap
Keywords
💡Integration by parts
💡Formula
💡Indefinite integration
💡Definite integration
💡Exam style questions
💡Derivative
💡Logarithmic function
💡Trigonometric functions
💡Antiderivatives
💡Limits
💡Practice
Highlights
Integration by parts is a method for integrating products of functions, particularly useful when one of the functions is easier to differentiate.
The formula for integration by parts is presented and explained, emphasizing the need to remember it for effective use.
The choice of 'u' and 'v' in the formula is crucial and often depends on which function can be more easily differentiated or integrated.
An example is given where 6x^2 is multiplied by ln(x), illustrating the process of choosing 'u' and 'v' and applying the formula.
The concept of 'u-substition' is introduced as a way to simplify the integral and make it easier to solve.
A second example involves integrating a function with both '3x' and 'e^(-x)', demonstrating the flexibility of choosing 'u' and 'v'.
Trigonometric functions are tackled in the third example, showing how to apply integration by parts to more complex functions like x^2 * sin(x).
The transcript explains the use of integration by parts multiple times when necessary, as shown in the trigonometric example.
A clever trick for integrating ln(x) is presented, using integration by parts to handle a function without a straightforward integral.
Definite integration using limits is demonstrated with an example, showing how to apply the integration by parts formula within a specific range.
The importance of simplifying the integral to a form that can be easily integrated is emphasized throughout the transcript.
An exam-style question is solved, giving learners insight into how integration by parts is applied in exam settings.
The transcript concludes with a reminder to practice with various examples to solidify understanding and application of integration by parts.
The presenter offers additional resources for learning, including online tuition, through their website and email.
The transcript encourages active learning by suggesting that learners pause, rewind, and work through examples at their own pace.
The use of 'u-dash' and 'v-dash' notation is introduced to denote the derivative of 'u' and 'v' for clarity in the integration process.
The transcript provides a step-by-step guide through each example, ensuring that learners can follow the logic and process of integration by parts.
The importance of recognizing when to apply integration by parts and choosing the correct functions for 'u' and 'v' is highlighted.
The concept of simplifying the integral by differentiating parts of the function is a recurring theme throughout the examples.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: