2011 Calculus BC free response #6a | AP Calculus BC | Khan Academy
TLDRThe video script discusses the Taylor series, a polynomial approximation of functions, with a focus on approximating sine of x and sine of x squared around x=0. It explains the process of deriving the first four non-zero terms of the Taylor series for sine of x and provides a simplified approach for sine of x squared by substituting x with x squared in the derived terms. The explanation is enriched with the concept of derivatives and their role in constructing the series.
Takeaways
- 📈 The Taylor series is a polynomial approximation of a function, useful for approximating complex functions with simpler polynomials.
- 🔍 To approximate a function around 0 with a Taylor series, one uses the function's derivatives at 0, evaluated at x and divided by the corresponding factorial.
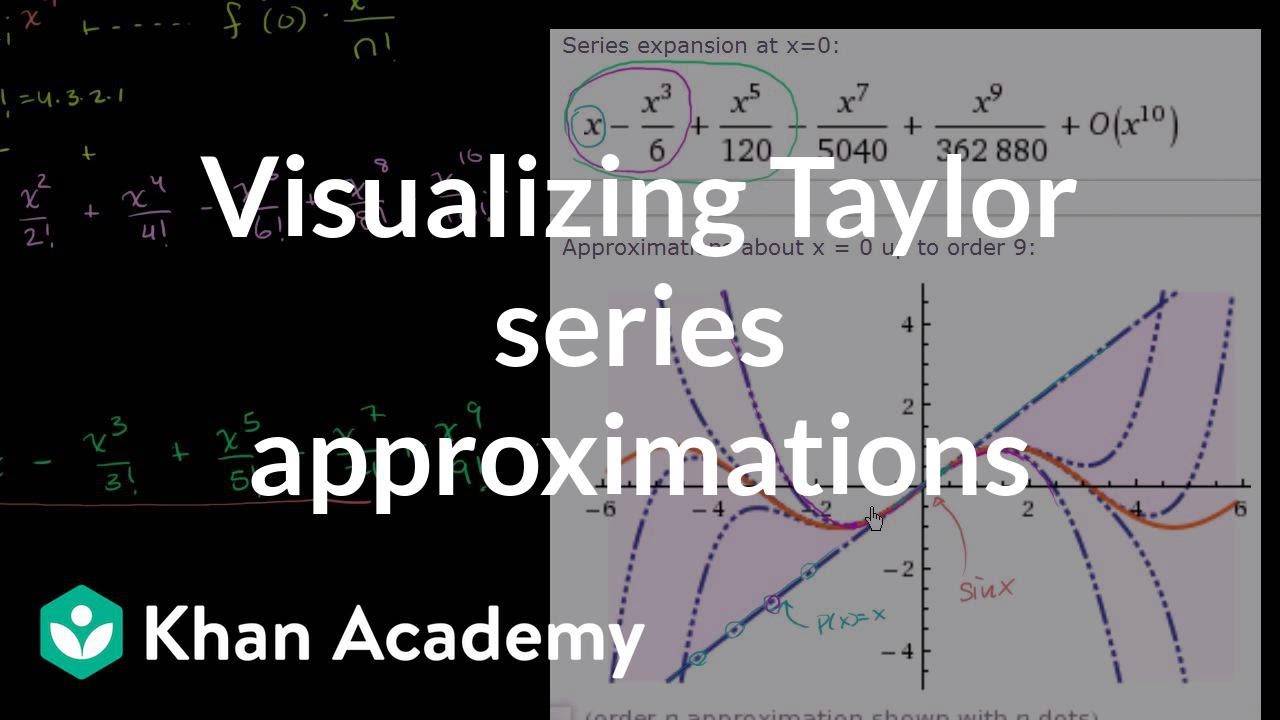
- 🌀 The first four non-zero terms of the sine function's Taylor series are given by: x - x^3/3! + x^5/5! - x^7/7!.
- 🔧 When finding the Taylor series for sine of x squared, it's more efficient to substitute x with x^2 in the sine of x Taylor series rather than taking derivatives of sine of x squared directly.
- 📌 The Taylor series for sine of x squared can be approximated as: x^2 - x^6/3! + x^10/5! - x^14/7!.
- 🔄 The derivatives of the sine function cycle every four derivatives, returning to the function itself, which is a property that can be used to simplify calculations.
- 📊 Euler's identity is referenced as a key formula in understanding the Taylor series for sine of x.
- 🧩 Each term in the Taylor series is derived from the function's derivatives at 0, showing the function's local behavior around a given point.
- 🔢 The Taylor series provides an increasingly accurate approximation of a function as more terms are added, potentially converging to the actual function with an infinite number of terms.
- 🎯 The first non-zero terms of a Taylor series are crucial for capturing the initial behavior of the function near the point of approximation.
- 🌟 The Taylor series is a powerful mathematical tool that bridges the gap between calculus and algebra, enabling the analysis of functions in terms of polynomials.
Q & A
What is a Taylor series?
-A Taylor series is a polynomial approximation of a function, used to represent a function as an infinite sum of terms calculated from the values of its derivatives at a single point.
How does the Taylor series approximation improve as more terms are added?
-As more terms are added to the Taylor series, the approximation becomes better and more closely resembles the actual function. With an infinite number of terms, the series may converge to the actual function.
What is the first term in the Taylor series for sine of x around x equals 0?
-The first term in the Taylor series for sine of x around x equals 0 is g(0), which is 0 since sine of 0 is 0.
What is the second non-zero term in the Taylor series for sine of x around x equals 0?,
-The second non-zero term is the product of the first derivative of sine at x=0 (which is cosine of 0, or 1), x, and the power of x, divided by 2! (which is 2). So, it is x.
What is the third non-zero term in the Taylor series for sine of x around x equals 0?
-The third non-zero term is the product of the third derivative of sine at x=0 (which is negative cosine of 0, or -1), x cubed, and the power of x divided by 3! (which is 6). So, it is -x^3/6 or -x^3/2.
What is the fourth non-zero term in the Taylor series for sine of x around x equals 0?
-The fourth non-zero term is the product of the fourth derivative of sine at x=0 (which is sine of 0, or 0), x to the fourth power, and the power of x divided by 4! (which is 24). However, since the fourth derivative at 0 is 0, this term is 0.
How can we find the Taylor series for sine of x squared around x equals 0?
-We can find the Taylor series for sine of x squared by substituting x with x squared in the Taylor series for sine of x. This simplifies the process of calculating derivatives.
What is the first non-zero term in the Taylor series for sine of x squared around x equals 0?
-The first non-zero term for sine of x squared is x squared, as we replace x with x squared in the sine of x Taylor series.
What is the second non-zero term in the Taylor series for sine of x squared around x equals 0?
-The second non-zero term is x squared to the third power divided by 3! (which is 6), or x^6/6, as we replace x with x squared in the third derivative term of the sine of x Taylor series.
What is the third non-zero term in the Taylor series for sine of x squared around x equals 0?
-The third non-zero term is x squared to the fifth power divided by 5! (which is 120), or x^10/120, as we replace x with x squared in the fifth derivative term of the sine of x Taylor series.
What is the fourth non-zero term in the Taylor series for sine of x squared around x equals 0?
-The fourth non-zero term is x squared to the seventh power divided by 7! (which is 5040), or x^14/5040, as we replace x with x squared in the seventh derivative term of the sine of x Taylor series.
Outlines
📚 Introduction to Taylor Series and Sine Function
This paragraph introduces the concept of Taylor series as a polynomial approximation of a function, specifically focusing on the sine function. It explains the process of finding the first non-zero terms for the Taylor series of sine x about x equals 0. The explanation includes a reminder of the Taylor series formula and its application around the point 0, using derivatives of the function at that point. The paragraph also demonstrates the calculation of the first four non-zero terms of the Taylor series for sine x by evaluating its derivatives at x=0.
🔢 Derivatives and Approximation of Sine Function
The second paragraph delves deeper into the calculation of the derivatives of the sine function and their use in approximating the function using the Taylor series. It provides a step-by-step breakdown of finding the third, fourth, and subsequent derivatives of sine x and their values at x=0. The paragraph also discusses the general pattern observed in the derivatives and how this pattern can be used to identify the non-zero terms in the Taylor series. Additionally, it presents a method for simplifying the process of finding the Taylor series for sine of x squared by replacing x with x squared in the terms of the sine x Taylor series.
Mindmap
Keywords
💡Taylor Series
💡Derivative
💡Sine Function
💡Cosine Function
💡Approximation
💡Trigonometric Functions
💡Polynomial
💡Function
💡Euler's Identity
💡Series
Highlights
Introduction to Taylor series as a polynomial approximation of functions.
Explanation of how a Taylor series can be used to approximate a function around a specific point, in this case, x=0.
Description of how the shape of the Taylor series changes with the addition of more terms.
The process of finding the first four non-zero terms of the Taylor series for sine of x.
Derivation of the Taylor series for sine of x using Euler's identity.
Explanation of the derivatives of sine of x and their values at x=0.
Method for finding the non-zero terms of the Taylor series for sine of x squared by substitution.
Simplification of the Taylor series for sine of x squared by replacing x with x squared in the series of sine of x.
The final approximation of the Taylor series for sine of x squared.
The concept of Taylor series and its application in approximating complex functions with polynomials.
The importance of understanding the derivatives of a function when constructing its Taylor series.
The cyclical nature of the derivatives of sine function and how it affects the Taylor series.
The step-by-step approach to calculating the Taylor series for a given function.
The practical application of Taylor series in improving the accuracy of function approximations by adding more terms.
The mathematical process of differentiating and evaluating derivatives at a specific point to construct a Taylor series.
The innovative method of simplifying the calculation of the Taylor series for sine of x squared by substitution instead of direct differentiation.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: