Calculus 3: Equations of Lines and Planes (Video #5) | Math with Professor V

Math with Professor V

3 Jun 202047:57

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus lecture delves into the equations of lines and planes, emphasizing the transition from 2D to 3D. It explains how a line in 3D space is defined by a point and a direction vector, leading to parametric equations. The lecture also covers the concept of skew lines, which neither intersect nor are parallel, and introduces planes defined by a point and a normal vector. It further explores the equations of planes, including scalar and vector forms, and discusses applications such as finding the distance from a point to a line or plane, and the intersection of lines and planes. The importance of visualizing and understanding these concepts is highlighted throughout the lesson.

Takeaways

📚 The video lecture is the fifth in a series on calculus, focusing on equations of lines and planes in three-dimensional space.
🗺 To define a line in 3D space, a point and a direction vector are required, with the direction vector replacing the concept of slope used in 2D.
🔍 The direction of a line in 3D is given by a vector, often represented by \( \vec{V} \), with components (a, b, c).
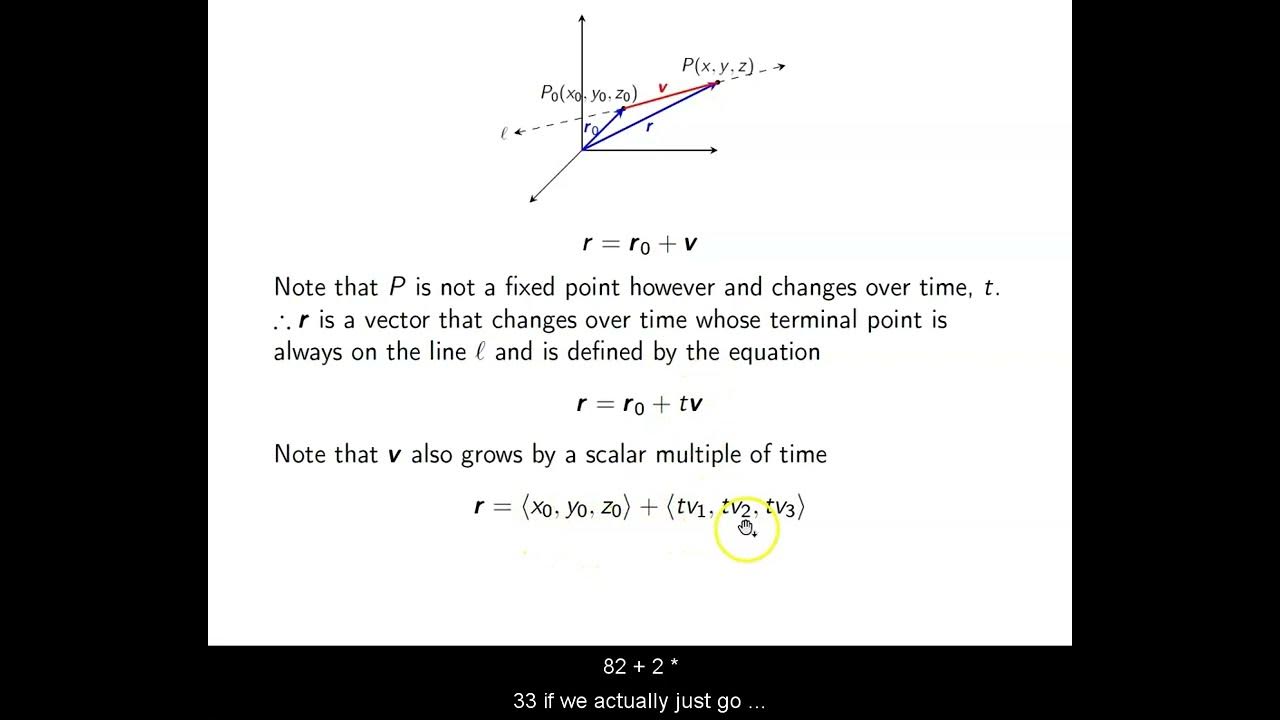
📍 The equation of a line can be expressed in vector form as \( \vec{R} = \vec{R_0} + t\vec{V} \), where \( \vec{R_0} \) is the position vector to a point on the line and \( t \) is a scalar.
📈 Parametric equations of a line are derived from the vector equation and are written as \( x = x_0 + at \), \( y = y_0 + bt \), and \( z = z_0 + ct \).
🔡 The components a, b, and c of the direction vector are also known as direction numbers and are crucial for writing the parametric equations of a line.
🔄 The parametric equations of a line are not unique and can vary depending on the choice of the initial point and direction vector.
✂️ Symmetrical equations of a line can be obtained by eliminating the parameter \( t \) from the parametric equations, resulting in a relationship between the differences in coordinates.
📐 To determine if two lines are parallel, check if their direction vectors are scalar multiples of each other; for perpendicularity, the dot product of the direction vectors should be zero.
🤔 Skew lines are non-parallel lines that do not intersect and are considered to lie in different planes, which is a concept unique to 3D space.
🛠 The distance from a point to a line can be found using the Pythagorean theorem, scalar projection, or trigonometric methods involving the cross product of vectors.

Q & A

What is the main difference between the direction of a line in a plane and in three-dimensional space?
-In a plane, the direction of a line can be described by a slope, which is a two-dimensional ratio. In three-dimensional space, the direction is described using a vector, known as the direction vector, because a two-dimensional ratio is not sufficient to provide direction in 3D.
What is a direction vector in the context of a line in three-dimensional space?
-A direction vector is a vector, usually denoted by V, that describes the direction of a line in three-dimensional space. It has components a, b, and c, which represent the direction ratios along the x, y, and z axes, respectively.
How can you find the equation of a line in three-dimensional space if you have a point and a direction vector?
-You can find the equation of a line by considering a point P₀ with coordinates (X₀, Y₀, Z₀) on the line and a direction vector V with components (a, b, c). The line equation can be written in parametric form as X = X₀ + at, Y = Y₀ + bt, and Z = Z₀ + ct, where t is a scalar parameter.
What are the parametric equations of a line, and how are they derived?
-Parametric equations of a line are a set of equations that express the coordinates of any point on the line as functions of a parameter. They are derived by starting with the position vector to a known point on the line, adding a scalar multiple of the direction vector, and equating the components to the variable coordinates (X, Y, Z).
How can you find two other points on a line given its parametric equations and a point on the line?
-You can find two other points on the line by choosing two different values for the parameter 't' in the parametric equations, excluding t = 0, which would just give the original point. Substituting these values into the parametric equations yields the coordinates of the new points.
What are the symmetric equations of a line, and how are they obtained?
-The symmetric equations of a line are an alternative form of the line equation that involves the ratios of the differences between the coordinates of any point on the line and a known point on the line, to the components of the direction vector. They are obtained by eliminating the parameter 't' from the parametric equations.
How can you determine if two lines in three-dimensional space are parallel?
-Two lines are parallel if their direction vectors are scalar multiples of each other. By comparing the direction vectors from the parametric or symmetric equations of the lines, you can determine if they are parallel.
What is a normal vector, and how is it used in the context of planes?
-A normal vector is a vector that is orthogonal to a plane. It is used to describe the direction of the plane and is essential for writing the equation of the plane. The normal vector has components that are the coefficients of the variables in the plane's scalar equation.
How can you find the equation of a plane given three points on the plane?
-To find the equation of a plane given three points, you first find two vectors on the plane by subtracting the coordinates of the points. Then, you take the cross product of these two vectors to find a normal vector to the plane. Finally, you use the normal vector and any of the three points to write the scalar equation of the plane.
What is the significance of the normal vector in determining the angle between two planes?
-The angle between two planes is defined as the angle between their normal vectors. The normal vectors provide a way to measure the orientation of the planes with respect to each other, and the angle between the vectors can be found using the dot product or the cross product.
How can you find the equation of the line of intersection of two planes?
-To find the line of intersection, you first identify a point on the line by observing or solving the equations of the two planes. Then, you find the direction vector of the line by taking the cross product of the normal vectors of the two planes. Finally, you write the parametric equations of the line using the point and the direction vector.
What is the method to find the distance from a point to a plane?
-The distance from a point to a plane is found by projecting the vector from the point to any point on the plane onto the normal vector of the plane. The absolute value of the scalar projection gives the shortest distance from the point to the plane.

Outlines

00:00

📚 Introduction to Calculus 3: Equations of Lines and Planes

This paragraph introduces the topic of the video lecture, focusing on the equations of lines and planes in three-dimensional space. It explains the transition from two-dimensional slope to three-dimensional direction vectors, which are essential for defining lines in space. The importance of a point and a direction vector in determining a line is highlighted, along with the conceptual framework for understanding the equation of a line in 3D space.

05:01

🔍 Parametric and Symmetric Equations of a Line

The paragraph delves into the specifics of writing the equation of a line in 3D space. It discusses the parametric equations derived from a point and a direction vector, and how to obtain points on the line by varying the parameter. The symmetric equations of a line are also introduced, which are an alternative representation that can be found by eliminating the parameter T from the parametric equations. The paragraph includes an example of finding parametric equations for a line given a point and a direction vector, and identifying additional points on the line.

10:04

📐 Understanding Direction Vectors and Parallel Lines

This section explores the concept of direction vectors and how they relate to the orientation of lines in space. It explains how to determine if two lines are parallel by comparing their direction vectors as scalar multiples. The conditions for lines to be perpendicular are also discussed, using the dot product of direction vectors to establish a right angle. The unique situation of skew lines, which neither intersect nor are parallel, is introduced with an example to illustrate the concept.

15:05

📏 Calculating the Distance from a Point to a Line

The paragraph presents methods for calculating the shortest distance from a point to a line, emphasizing the importance of visualizing and understanding the geometric relationships involved. It outlines three approaches: using the Pythagorean theorem, the orthogonal projection of a vector, and trigonometric relationships involving the sine of the angle between vectors. The paragraph challenges the viewer to verify the correctness of the methods and to calculate the distance, providing an exercise to reinforce learning.

20:05

🏗️ The Equation of a Plane and Its Normal Vector

This section introduces the concept of planes in three-dimensional space, focusing on the role of a normal vector in defining the plane's orientation. It explains the vector form of the equation of a plane and transitions to the scalar equation, which is commonly used in applications. The process of finding the equation of a plane given a point and a normal vector is demonstrated, along with an example that includes graphing the plane by plotting its traces in the coordinate planes.

25:09

🔄 Deriving Plane Equations from Points and Vectors

The paragraph discusses the method of determining a plane's equation using three points in the plane. It describes how to find a normal vector to the plane by taking the cross product of two vectors derived from the points. The process is illustrated with an example that shows how to calculate the normal vector, derive the scalar equation of the plane, and present it in a linear standard form.

30:10

🔄 Finding the Equation of a Plane Containing a Line

This section presents a method for finding the equation of a plane that contains a given line and passes through a specific point. It explains the process of using the direction vector of the line and a vector between the given point and a point on the line to find a normal vector to the plane through the cross product. The example provided walks through the steps of deriving the plane's equation and sketching it.

35:11

📍 Intersection of Two Planes and Their Angle

The paragraph explores the concept of the intersection of two planes, which results in a straight line. It explains how to find the equation of this line of intersection by identifying a point common to both planes and determining the direction vector by taking the cross product of the normals of the two planes. The relationship between the angle between the planes and the angle between their normal vectors is also discussed.

40:12

📏 Distance from a Point to a Plane

This final paragraph concludes the lesson by addressing the calculation of the distance from a point to a plane. It emphasizes the importance of understanding the geometric concept behind the calculation rather than memorizing formulas. The method involves projecting a vector from the point to the plane along the normal vector to the plane and taking the absolute value of this projection as the distance. An example is provided to illustrate the process clearly.

Mindmap

Keywords

💡Equation of a Line

The equation of a line is a mathematical representation that defines the relationship between coordinates of any point on the line. In the video, the equation of a line is discussed in the context of 3-dimensional space, where a point and a direction vector are used to determine the line's path. The script explains how to derive parametric equations of a line using a point and a direction vector, which are essential for understanding the position and orientation of lines in space.

💡Direction Vector

A direction vector is a vector that indicates the direction of a line in space. It is denoted by the letter 'V' in the script and has components (a, b, c) that represent the direction ratios along the x, y, and z axes, respectively. The concept is fundamental to defining the orientation of a line in 3D space, as it provides the necessary information for the line's trajectory beyond the two-dimensional slope concept.

💡Parametric Equations

Parametric equations are a set of equations that express the coordinates of points in a space using a parameter, often denoted by 't'. In the video, parametric equations are used to describe the position of any point on a line in 3D space relative to a known point and a direction vector. The script provides an example of how to derive these equations for a line given a point and a direction vector.

💡Symmetric Equations

Symmetric equations of a line are derived from parametric equations by eliminating the parameter 't'. They provide a relationship between the differences in coordinates of any point on the line and the components of the direction vector. The script explains how to obtain symmetric equations and mentions their utility in certain contexts, such as when one of the direction numbers is zero.

💡Normal Vector

A normal vector is a vector that is perpendicular to a plane. It is crucial for defining the orientation of a plane in 3D space. In the script, the normal vector 'n' is used to describe the plane's direction and is essential for writing the plane's equation. The normal vector's components are derived from the coefficients of the plane's equation.

💡Scalar Equation of a Plane

The scalar equation of a plane is an algebraic equation that represents the plane in 3D space. It is derived from the dot product of the normal vector and the position vector of any point on the plane equated to zero. The script illustrates how to obtain the scalar equation from the normal vector components and a point on the plane.

💡Cross Product

The cross product is a mathematical operation that takes two vectors and returns a third vector that is perpendicular to the plane containing the original vectors. In the video, the cross product is used to find the normal vector to a plane when given two vectors lying in the plane, which is essential for determining the plane's orientation.

💡Distance from a Point to a Line

The distance from a point to a line is the shortest distance between a given point and any point on the line. The script discusses three methods to calculate this distance: using the Pythagorean theorem, the orthogonal projection of a vector, and the sine of the angle between the point and the line, which is derived from the cross product of vectors.

💡Skew Lines

Skew lines are two lines that are neither parallel nor intersecting. They exist in different planes and do not share any common points. The script explains how to determine if two lines are skew by checking if they are not parallel and do not intersect, using their parametric equations.

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two vectors and returns a scalar. It is used to determine the angle between two vectors and to check if vectors are perpendicular. In the script, the dot product is used to verify if two lines are perpendicular and to calculate the distance from a point to a plane.

💡Plane Intersection

The intersection of two planes is the set of points that both planes share. If the planes are not parallel, their intersection is a line. The script explains how to find the line of intersection by using a point on the line and the direction vector, which is found by taking the cross product of the normal vectors of the two planes.

Highlights

Introduction to the concept of equations of lines and planes in three-dimensional space.

Explanation of the insufficiency of the two-dimensional slope for direction in 3D space, necessitating the use of a direction vector.

Description of the direction vector 'V' with components (a, b, c) for determining the direction of a line in space.

Method to write the equation of a line using a point and a direction vector in parametric form.

Understanding the relationship between the position vector and the direction vector for any point on a line.

Derivation of parametric equations of a line given a point and a direction vector.

Practice example: Finding parametric equations of a line and identifying points on the line.

Discussion on the non-uniqueness of parametric equations for a line and how different initial points can yield different equations.

Introduction to symmetric equations of a line as an alternative representation.

Explanation of how to determine if two lines are parallel by comparing their direction vectors.

Method to determine if two lines are perpendicular using the dot product of their direction vectors.

Concept of skew lines and how to determine if two non-parallel lines are skew or intersecting.

Example of determining the intersection point or confirming skew lines using a system of equations.

Approaches to finding the distance from a point to a line using Pythagorean theorem, orthogonal projection, and trigonometric methods.

Introduction to the concept of planes determined by a point and a normal vector.

Explanation of the vector form and scalar form of the equation of a plane.

Method to find the equation of a plane given three points or a point and a normal vector.

Application of the cross product to find a normal vector to a plane given two vectors in the plane.

Process for sketching a plane by graphing its traces in the coordinate planes.

Determination of the line of intersection between two planes using their normal vectors and a point on each plane.

Method to find the distance from a point to a plane using vector projection and the normal vector of the plane.

Transcripts

Browse More Related Video

Ch. 9.6 Equations of Lines and Planes

Lec 5: Parametric equations for lines and curves | MIT 18.02 Multivariable Calculus, Fall 2007

What is a tangent plane

Equations of Planes: Vector & Component Forms | Multivariable Calculus

Calculus 3: Lecture 11.5 Lines and Planes in Space

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V

Related Tags

Calculus 3 Equations Lines Planes Direction Vector Normal Vector Parametric Equations Symmetric Equations Distance Calculation 3D Geometry Vector Analysis