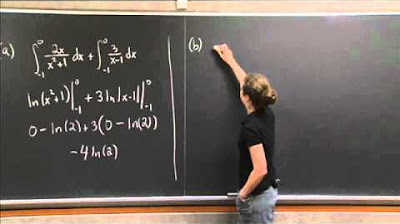Partial Fractions (Non-Repeating Linear Factors)

turksvids
25 May 201305:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial demonstrates the technique of partial fractions for evaluating integrals, particularly useful for integrals where substitution doesn't work out. The instructor shows step-by-step how to decompose fractions and use the 'cover-up' method to find the values of A and B. Two examples are given, one with a quadratic and another with a cubic polynomial, illustrating how to rewrite the integrand and simplify the integral into manageable parts, making it easier to solve.

Takeaways
  • 📚 Partial fractions are a technique used for integrating functions where substitution doesn't work out well.
  • 🔍 The method involves completely factoring the denominator and decomposing the fraction into simpler parts.
  • 📝 Proper fractions are used, which means the numerators should not have terms that could be factored out.
  • 🧩 The process includes finding constants 'a' and 'b' by setting x to values that simplify the equation and solving for the unknowns.
  • 🔑 The 'cover-up method' is introduced as a shortcut to find the values of 'a' and 'b' without fully clearing the denominator.
  • 📉 The script demonstrates the use of partial fractions with an example involving the integral of (x^2 - 2x - 3) / (x^2 - x - 6).
  • 📈 Another example is given with a cubic polynomial divided by a quadratic, showing how to factor and decompose the fraction.
  • 📝 The values of 'a', 'b', and 'c' are determined for the second example using both direct substitution and the cover-up method.
  • 📚 The integrals are then rewritten using the values of 'a', 'b', and 'c', resulting in simpler integrals that can be solved using natural logarithms.
  • 🔑 The script emphasizes the importance of practicing the cover-up method for proficiency in partial fraction decomposition.
  • 🎓 The video concludes by summarizing the steps taken and encouraging viewers to apply these techniques to similar problems.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the use of partial fractions to evaluate integrals in calculus.

  • Why is the partial fractions technique useful?

    -The partial fractions technique is useful when substitution doesn't work out and you have integrals that look like they should be solvable by substitution.

  • What is the first example integral given in the video?

    -The first example integral given is \( \int \frac{x^2 - 2x - 3}{(2x - 2)} du \), where \( u \) is a placeholder for the denominator after factoring.

  • What is the process of decomposing a fraction in partial fractions?

    -The process involves expressing the fraction as a sum of simpler fractions with common denominators, such as \( \frac{ax - 3}{(x - 3)(x + 1)} \).

  • What is the 'cover-up method' mentioned in the video?

    -The 'cover-up method' is a technique used to find the values of A and B in partial fractions by covering up part of the denominator and substituting values to simplify the equation.

  • How does the video demonstrate finding the value of 'a' in the first example?

    -The video sets \( x = 3 \) to make the term with B disappear, then solves the resulting equation to find that \( a = 3 \).

  • How does the video demonstrate finding the value of 'b' in the first example?

    -The video sets \( x = -1 \) to make the term with A disappear, then solves the resulting equation to find that \( b = 2 \).

  • What is the second integral example given in the video?

    -The second example integral is \( \int \frac{x^3 + 3x^2 - 10x}{x} \) after factoring out an \( x \).

  • How many parts does the second integral example break down into?

    -The second integral example breaks down into three parts after factoring the quadratic and setting up partial fractions.

  • What are the values of A, B, and C found in the second example?

    -In the second example, the values found are \( A = -\frac{2}{5} \), \( B = -\frac{1}{35} \), and \( C = \frac{3}{7} \).

  • How does the video conclude the process of solving the integrals using partial fractions?

    -The video concludes by rewriting the original integrals into simpler integrals using the found values of A, B, and C, and then solving those simpler integrals.

Outlines
00:00
📚 Introduction to Partial Fractions for Integrals

This paragraph introduces the concept of partial fractions as a technique for evaluating integrals that don't lend themselves to straightforward substitution. The speaker demonstrates the method using the example of an integral with a quadratic denominator that can be factored. The process involves decomposing the fraction into simpler terms with a common denominator, which is then used to find the constants 'a' and 'b' by substituting specific values of 'x' that simplify the equation. The 'cover-up' method is introduced as a shortcut to determine these constants without fully clearing the denominator. The speaker concludes by rewriting the original integral using the values of 'a' and 'b' found, transforming it into a sum of natural logarithms that are easier to integrate.

05:03
🔍 Applying Partial Fractions to a Cubic Integral

In this paragraph, the speaker applies the partial fractions technique to a more complex integral involving a cubic polynomial in the numerator and a factored quadratic in the denominator. The process begins by factoring out 'x' and then factoring the remaining quadratic expression. The integral is then broken down into three separate fractions, each with a different factor in the denominator. The 'cover-up' method is used again to quickly determine the constants 'a', 'b', and 'c' by substituting values of 'x' that zero out the other terms. The speaker then demonstrates the verification of these constants by clearing the denominator and solving for each constant individually. Finally, the original integral is rewritten as a sum of three simpler integrals, each of which can be solved using standard integration techniques.

Mindmap
Keywords
💡Partial Fractions
Partial fractions is a mathematical technique used to decompose a complex fraction into simpler fractions, each with a simpler denominator. In the context of the video, it is used to simplify the process of integrating functions where substitution might not work directly. The script mentions using partial fractions to evaluate integrals and demonstrates how to decompose fractions into simpler forms to facilitate integration.
💡Integration
Integration is a fundamental operation in calculus, which involves finding the antiderivative of a function. The video script discusses using partial fractions to evaluate integrals, which is a method to simplify complex integrals into more manageable forms. The script provides examples of how integrals can be rewritten using partial fractions, making them easier to solve.
💡Substitution
Substitution is a common technique in calculus used to simplify the process of integration by replacing a part of the function with a new variable. In the script, the speaker mentions that partial fractions are useful when substitution does not work out as expected, indicating that partial fractions provide an alternative approach when direct substitution is not feasible.
💡Denominator
The denominator in a fraction is the expression that appears in the bottom part of the fraction line. In the context of the video, the speaker discusses factoring the denominator to facilitate the use of partial fractions. The script provides examples of how the denominator is factored and used in the process of decomposing fractions.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of its factors. The video script emphasizes the importance of factoring the denominator of a fraction when using partial fractions. Factoring allows for the decomposition of the fraction into simpler terms, which is crucial for the integration process.
💡Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm to the base e. In the video script, after decomposing the fraction using partial fractions, the speaker shows how the resulting integrals can be expressed in terms of natural logarithms. This simplifies the process of finding the antiderivative of the original function.
💡Cover Up Method
The cover up method is a technique mentioned in the script for determining the coefficients in partial fractions. It involves covering the part of the denominator that would make it zero and substituting that value to solve for the coefficients. The script demonstrates this method by covering parts of the denominator and substituting values to find the values of A and B.
💡Coefficients
Coefficients are numerical factors in algebraic expressions that multiply variables. In the context of partial fractions, coefficients are the constants that multiply the variables in the decomposed fractions. The script discusses how to determine these coefficients, such as A and B, through the process of partial fractions.
💡Antiderivative
The antiderivative is a function whose derivative is the original function. The video script discusses finding the antiderivative of a function by first rewriting it using partial fractions, which simplifies the integration process. The script provides examples of how the antiderivative can be found after decomposing the fraction.
💡Quadratic
A quadratic is a polynomial of degree two. In the script, the speaker mentions factoring a quadratic polynomial in the denominator of a fraction. This is an example of how factoring can be used in the process of partial fractions to simplify the integration of a function.
Highlights

Introduction to using partial fractions to evaluate integrals, a useful technique when substitution doesn't work out.

Demonstration of how to decompose a fraction with a quadratic denominator into partial fractions.

Clear explanation of proper fractions and the importance of long division before applying partial fractions.

Illustration of the process to clear the denominator and find the values of a and b by substituting specific x values.

Introduction of the 'cover-up method' as an alternative and efficient way to find the values of a and b.

Step-by-step guide on how to apply the cover-up method to find the coefficients of the partial fractions.

Explanation of how to rewrite the original integrand using the values of a and b found through partial fractions.

Application of partial fractions to a second example with a cubic polynomial in the numerator and a factored quadratic denominator.

Demonstration of breaking down the integrand into three parts that could have been multiplied to get the common denominator.

Use of the cover-up method to quickly find the values of a, b, and c for the second example without clearing the denominator.

Verification of the values found using the cover-up method by substituting specific x values and solving for the coefficients.

Finalization of the problem by rewriting the original integrand into three simpler integrals using the values of a, b, and c.

Emphasis on the simplicity of the resulting integrals after applying partial fractions, making them easier to solve.

Highlighting that partial fractions work best with non-repeating linear factors, which is arguably the easiest type.

Conclusion with a hope that the explanation was helpful and wishing good luck to the viewers in applying the technique.

Transcripts

Browse More Related Video

Partial Fraction Decomposion

Lesson 7 - Integration By Partial Fractions (Calculus 2 Tutor)

Changing the Order of Integration (Double Integrals)

Integration By Parts

Cover-Up Method for Partial Fraction Decomposition

Integration Practice I | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Partial FractionsIntegralsMathematicsCalculusEducationFactorizationIntegral TechniquesAlgebraTutorialProblem Solving