19. Intro Partial DIfferential Equations (PDEs)
TLDRThis lecture delves into the world of partial differential equations (PDEs), distinguishing them from ordinary differential equations by their multivariable nature. It highlights the prevalence of PDEs in physics and engineering, where they model fields like pressure and temperature that vary over space and time. The speaker introduces the three main types of PDEs: elliptic, parabolic, and hyperbolic, exemplified by Poisson's, heat, and wave equations, respectively. The importance of initial and boundary conditions for solving PDEs is emphasized, along with the different types of boundary conditions: Dirichlet, Neumann, and mixed. The lecture suggests starting with Poisson's and Laplace's equations for a foundational understanding of solving PDEs.
Takeaways
- 📚 The lecture introduces the concept of partial differential equations (PDEs) and distinguishes them from ordinary differential equations by their handling of multiple independent variables.
- 🔍 PDEs are essential for describing fields in physics that depend on space and time, such as pressure and temperature, which vary continuously.
- 🌐 Most dynamical equations in physics are PDEs due to the three-dimensional nature of space and the inclusion of time.
- 🛠 Engineering often involves solving PDEs, which require different techniques from those used for ordinary differential equations, like the Runge-Kutta method.
- 📐 PDEs are categorized into elliptic, parabolic, and hyperbolic types based on the arrangement and signs of their derivatives in the equation.
- 📘 Elliptic PDEs, like Poisson's equation, have all second-order derivatives on one side of the equation with positive coefficients.
- 🔥 Parabolic PDEs, such as the heat equation, mix second and first-order derivatives, often representing diffusion processes.
- 🌊 Hyperbolic PDEs, exemplified by the wave equation, separate space and time derivatives, indicating wave-like behavior.
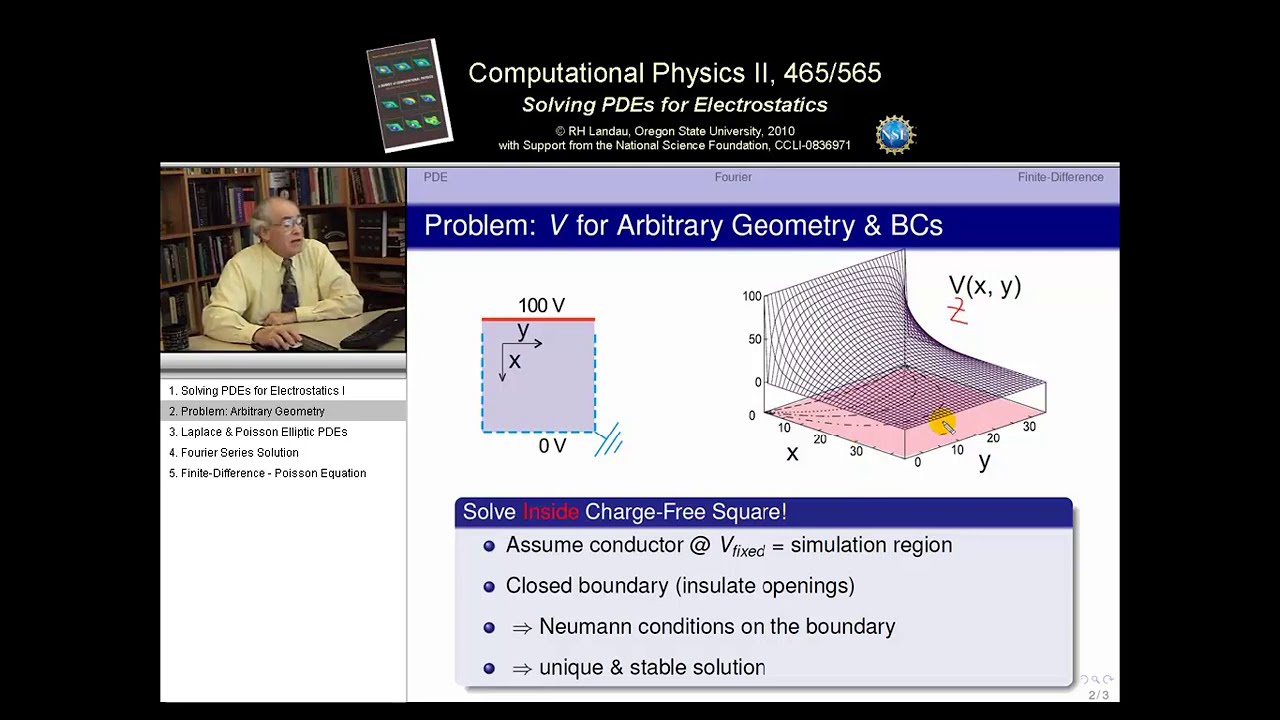
- 📝 To solve PDEs, both initial and boundary conditions are necessary, with the number of conditions correlating to the number of variables in the equation.
- 🚧 Boundary conditions can be Dirichlet, where the function value is known on the boundary, or Neumann, where the derivative is known, affecting the solvability and uniqueness of the solution.
- ⚠️ Overdetermined problems with too many boundary conditions may not have a solution, while underspecified problems may have an infinite number of solutions depending on assumptions made.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is an introduction to partial differential equations (PDEs), including their types and how to approach solving them.
What is the fundamental difference between ordinary differential equations and partial differential equations?
-The fundamental difference is that ordinary differential equations deal with one independent variable, while partial differential equations deal with more than one independent variable.
Why are differential equations used to describe fields in physics?
-Differential equations are used because they can describe how changes in the field at any point in space-time tend to influence neighboring points, which is a natural way to represent continuous variations in physical quantities like pressure and temperature.
What are the three basic types of partial differential equations?
-The three basic types of PDEs are elliptic, parabolic, and hyperbolic.
What is an elliptic partial differential equation?
-An elliptic PDE is characterized by the discriminant (a product of ac minus b squared) being greater than zero, with all second derivatives on the same side of the equation and having the same sign.
How is the Poisson's equation related to elliptic PDEs?
-Poisson's equation is an example of an elliptic PDE, where the second derivatives are all on the same side with positive signs.
What is a parabolic PDE and an example of it?
-A parabolic PDE has second derivatives on one side and a first-order derivative on the other side, with a positive sign. An example is the heat equation.
What is a hyperbolic PDE and what is a typical example?
-A hyperbolic PDE has space derivatives on one side and a time derivative on the other, both with positive signs. The wave equation is a typical example of a hyperbolic PDE.
Why are boundary conditions important in solving PDEs?
-Boundary conditions are important because they, along with initial conditions, are required to have unique solutions to the PDEs. They describe the physical situation and what is happening on the boundary of the problem domain.
What are the different types of boundary conditions mentioned in the script?
-The script mentions Dirichlet, Neumann, and Cauchy boundary conditions as different types that can occur in solving PDEs.
Why might an overdetermined problem be problematic when solving PDEs?
-An overdetermined problem is problematic because it may demand too much information, making it difficult or impossible to find a solution that satisfies all the given conditions.
What is the recommendation for further study after this introductory lecture on PDEs?
-The recommendation is to first look at the lecture on Poisson's equation, Laplace's equation, and static electric fields, as they are simple examples that demonstrate basic techniques for solving PDEs.
Outlines
📚 Introduction to Partial Differential Equations (PDEs)
The script begins with a welcome back to the office in western Oregon and an apology for potential interruptions due to hay fever. The lecturer introduces the topic of partial differential equations (PDEs), explaining the fundamental difference between ordinary differential equations (ODEs) and PDEs. PDEs are highlighted as essential for describing fields in physics that depend on multiple variables such as space and time. The importance of PDEs in physics and engineering is emphasized, and the need for different techniques to solve PDEs compared to ODEs is discussed. The session aims to provide an overview of how to solve PDEs, their types, and the development of algorithms for their solutions.
🔍 Exploring Types and Characteristics of PDEs
The second paragraph delves into the different forms of PDEs, focusing on second-order equations which are most common in nature. The general form of a second-order PDE is presented, with arbitrary functions and constants that can vary based on space and time. The paragraph explains how the values of these constants determine the type of PDE: elliptic, parabolic, or hyperbolic. Elliptic PDEs, like Poisson's equation, have all second derivatives on one side with a positive sign. Parabolic PDEs, exemplified by the heat equation, mix first and second derivatives. Hyperbolic PDEs, such as the wave equation, separate space and time derivatives. The lecturer suggests memorizing these types by associating them with specific physical equations.
📉 Boundary Conditions and Solutions for PDEs
The final paragraph discusses the necessity of initial and boundary conditions for solving PDEs, noting that more information is required due to the multiple variables involved. Boundary conditions are crucial for defining the physical situation and ensuring unique solutions. The types of boundary conditions—Dirichlet, Neumann, and a combination of both (Cauchy)—are explained, with emphasis on their role in determining the solvability and uniqueness of PDEs. The paragraph also touches on the implications of underspecified and overdetermined problems, suggesting that a well-defined physics problem should have a solution, but assumptions about boundary conditions can influence the nature of that solution. The lecturer concludes by recommending a lecture on Poisson's equation as a starting point for understanding basic techniques for solving PDEs.
Mindmap
Keywords
💡Partial Differential Equations (PDEs)
💡Ordinary Differential Equations (ODEs)
💡Differential Equations
💡Field
💡Elliptic PDEs
💡Parabolic PDEs
💡Hyperbolic PDEs
💡Boundary Conditions
💡Initial Conditions
💡Dirichlet Boundary Condition
💡Neumann Boundary Condition
Highlights
Introduction to partial differential equations (PDEs) and their importance in physics and engineering.
Difference between ordinary and partial differential equations: the latter deals with more than one independent variable.
Physical quantities like pressure and temperature vary continuously in space and time, making PDEs a natural choice for their description.
Most dynamical equations in physics are PDEs due to the three-dimensional nature of space and time.
The need for different techniques to solve PDEs compared to ordinary differential equations.
Explanation of the general form of second-order partial differential equations with arbitrary functions.
Definition and characteristics of elliptic PDEs, including the discriminant condition.
Poisson's equation as an example of an elliptic PDE.
Characteristics of parabolic PDEs, such as the heat equation, with a mix of first and second derivatives.
Definition and examples of hyperbolic PDEs, including the wave equation.
Importance of initial and boundary conditions for solving PDEs and ensuring unique solutions.
Types of boundary conditions: Dirichlet, Neumann, and mixed boundary conditions.
Requirements for boundary conditions specific to elliptic, parabolic, and hyperbolic PDEs.
Potential issues with underspecified or overdetermined problems in PDEs.
Emphasis on the importance of understanding the assumptions made in boundary conditions for PDEs.
Suggestion to start with Poisson's and Laplace's equations for understanding basic techniques in solving PDEs.
Conclusion of the introductory lecture on PDEs with a focus on practical applications and problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: