19.4 Electrostatic II

rubinhlandau

30 Aug 202037:15

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into solving partial differential equations with a focus on electrostatics, introducing the relaxation technique for Laplace's and Poisson's equations. The method involves discretizing the equations on a lattice and approximating derivatives with finite differences. The script covers the Jacobi and Gauss-Seidel methods, as well as the Successive Over-Relaxation (SOR) technique for enhancing convergence speed. Practical applications include analyzing electric fields in non-ideal capacitors, with exercises encouraging students to experiment with various geometries and boundary conditions to understand field distributions and charge accumulations.

Takeaways

📚 The lecture focuses on solving partial differential equations (PDEs), specifically Laplace's and Poisson's equations, using relaxation techniques.
🔍 Laplace's and Poisson's equations are used in electrostatics, with the latter accounting for charge presence where the former does not.
💻 The technique of discretizing the problem on a lattice and expressing derivatives as finite differences is fundamental to solving these equations numerically.
🧩 The finite difference method is contrasted with the finite element method, which is not covered in this lecture but is an 'industrial strength' technique.
🔑 Central difference approximation is highlighted as a key method for approximating the second derivative, which is crucial for solving the PDEs.
🔄 Iterative methods such as Jacobi, Gauss-Seidel, and Successive Over-Relaxation (SOR) are discussed as ways to improve the convergence of the solution.
🌐 Boundary conditions are essential for solving PDEs numerically, and the surrounding box or 'infinity' in the numerical model plays a critical role in determining the solution.
🔋 Realistic capacitor problems are introduced, including those with fringing fields and thick plates, which require solving for potential and charge distribution.
📈 The script encourages students to experiment with different geometries and boundary conditions to understand the effects on potential and electric field distribution.
📉 The importance of checking for convergence in numerical solutions is emphasized, suggesting the use of a trace along the diagonal as a measure of solution progress.
🛠️ The electric field can be visualized and calculated from the potential using numerical methods, with the gradient of the potential providing the field direction and magnitude.

Q & A

What is the main focus of the lecture series on solving partial differential equations?
-The lecture series focuses on solving partial differential equations, starting with simple cases in electrostatics and using fundamental techniques like relaxation for solving Laplace's or Poisson's equations.
What is the difference between Laplace's equation and Poisson's equation?
-Laplace's equation is a second-order partial differential equation with zero charge, while Poisson's equation includes a term for charge, making it a non-homogeneous equation.
How is the solution to Laplace's or Poisson's equation approached in the lecture?
-The solution is approached by discretizing the problem on a lattice and expressing derivatives as finite differences of the potential at lattice points, resulting in a system of algebraic equations.
What is the relaxation technique mentioned in the script?
-Relaxation is a numerical method used to solve systems of equations by iteratively updating the values of the variables until convergence is achieved. It's a fundamental technique for solving partial differential equations on a lattice.
Why is a surrounding box necessary in the numerical solution of these equations?
-A surrounding box is necessary to represent the boundary conditions at infinity, ensuring that the potential vanishes at the edges and providing a unique solution to the problem.
What is the Jacobi method and how does it relate to the relaxation technique?
-The Jacobi method is a simple relaxation technique where the new value of the potential at each lattice point is calculated using the old values of the surrounding points. It maintains the symmetry of the boundary conditions.
What is the Gauss-Seidel method and how does it differ from the Jacobi method?
-The Gauss-Seidel method is an improved relaxation technique where the updated value of the potential is used as soon as it is calculated for the neighboring points. This can lead to faster convergence compared to the Jacobi method.
What is the concept of successive over-relaxation (SOR) mentioned in the script?
-Successive over-relaxation is an advanced relaxation technique that involves adding a weighted residual (the correction term) to the old solution to speed up convergence. The weight is a parameter omega, which if greater than 1, can accelerate convergence but may also lead to instability.
How can one visualize the electric field from the potential in the context of this lecture?
-The electric field can be visualized by calculating its components as the first derivatives of the potential. This can be done using central difference approximations for the derivatives and then plotting the field arrows or lines perpendicular to the equipotential surfaces.
What practical applications are suggested in the script for the relaxation technique?
-The script suggests exploring non-ideal capacitor situations, such as capacitors with thick plates or dielectric materials, and analyzing the fringe and edge effects, as well as the charge accumulation. It also encourages comparing numerical solutions to analytical ones, like Fourier series.

Outlines

00:00

🔍 Introduction to Solving PDEs with Relaxation Technique

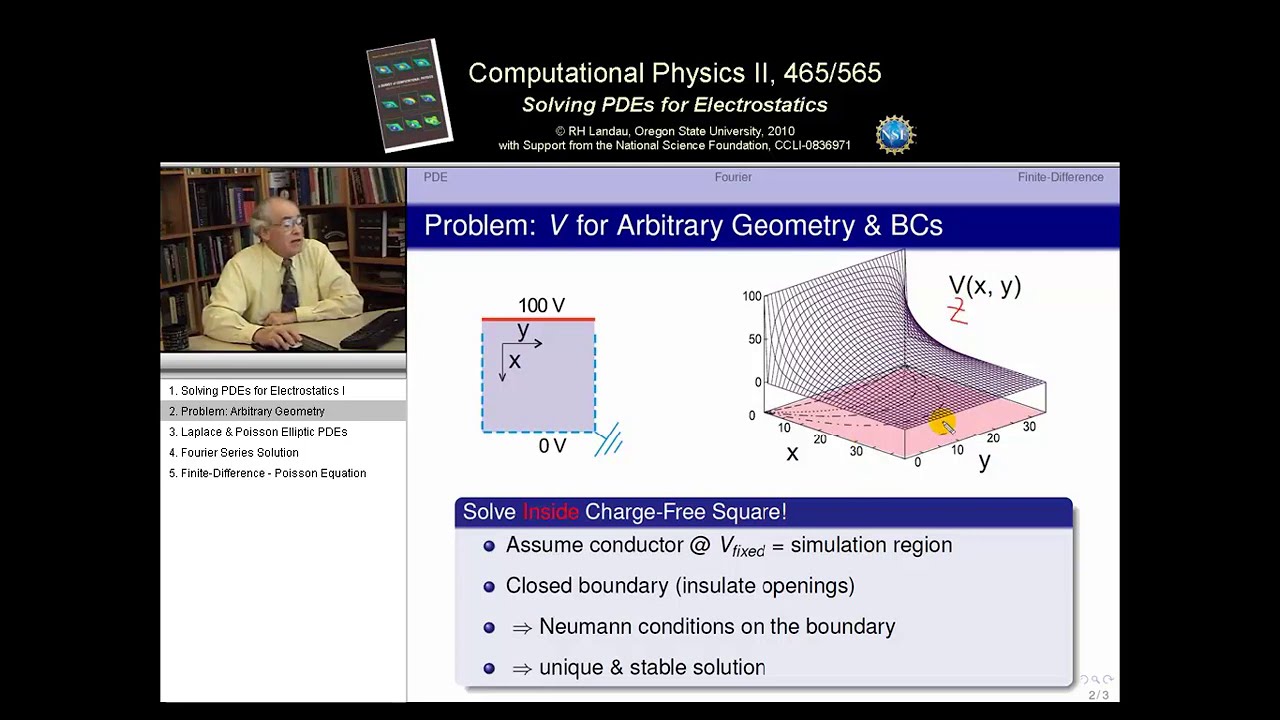
The lecture begins with an introduction to solving partial differential equations (PDEs), specifically focusing on electrostatics using a fundamental technique known as relaxation. The method involves discretizing the problem on a lattice and expressing derivatives as finite differences. The goal is to solve Laplace's or Poisson's equation, which differ by the presence of charge in the latter. The lecture also mentions an alternative technique, finite elements, which will be discussed in a separate session.

05:03

📚 Derivation of Finite Difference Equations for PDEs

This paragraph delves into the process of converting PDEs into finite difference equations by using Taylor series to approximate second derivatives. The approach involves adding series expansions for small variations around lattice points to cancel out odd terms, leaving a central difference approximation for the second derivative. This method results in algebraic equations that can be solved iteratively, with the potential at lattice points converging to the solution.

10:06

🔧 Solving Finite Difference Equations with Relaxation

The lecturer explains how to solve the finite difference equations obtained from PDEs using relaxation techniques. The method involves expressing the potential at a point as the average of surrounding values plus a density term. The solution is improved iteratively, with each iteration spreading the influence of boundary conditions into the interior. The process is likened to a 'relaxation' of the potential values towards the solution.

15:07

🚀 Exploring Relaxation Techniques: Jacobi, Gauss-Seidel, and SOR

This section discusses different variations of the relaxation technique, including the Jacobi method, which maintains boundary condition symmetry, and the Gauss-Seidel method, which uses updated values for faster convergence. The paragraph also introduces the concept of successive over-relaxation (SOR), which can further speed up convergence by adjusting a parameter called omega. The choice of omega is empirically determined to maximize speed while maintaining stability.

20:09

🛠 Implementing Relaxation Techniques in Practice

The script outlines the practical implementation of relaxation techniques through a program called 'laplace line' available in various programming languages. The program uses a 100x100 lattice and applies boundary conditions to iteratively solve for the potential within the lattice. The paragraph emphasizes the simplicity of the core algorithm and encourages students to study, compile, and modify the program to understand its convergence properties.

25:10

🔋 Investigating Realistic Capacitors and Electric Fields

The lecture moves on to apply the relaxation technique to more complex and realistic scenarios, such as capacitors with finite size and non-uniform fields. It discusses the concept of fringing fields and the importance of a surrounding box to represent boundary conditions at infinity. The paragraph also suggests exploring the effects of plate thickness and dielectric materials on the electric field and potential distribution.

30:11

🌐 Advanced Exploration: Charge Density and Electric Field Visualization

This section encourages students to go beyond solving for potential and to use the obtained solutions to calculate charge densities and visualize electric fields. It discusses the use of Poisson's equation to determine charge distribution and the visualization of electric fields using software packages. The paragraph highlights the importance of understanding how electric fields are derived from potential surfaces and the practical applications of these concepts.

35:14

📉 Assessing Numerical Solutions and Electric Field Calculations

The final paragraph focuses on how to assess the numerical solutions obtained using the relaxation technique. It suggests using the potential along the diagonal of the lattice as a measure to monitor convergence and to compare the numerical solution with analytical methods, such as Fourier series. The paragraph also emphasizes the importance of visualizing electric fields and understanding the limitations of different plotting packages in doing so.

🌟 Conclusion and Future PDE Discussions

The lecture concludes with a summary of the tasks accomplished and a preview of future topics. It highlights the practicality of the relaxation technique for solving electric field problems and encourages students to apply the method to various geometries. The lecturer also hints at upcoming discussions on different types of PDEs, signaling a continuation of the learning journey.

Mindmap

Keywords

💡Partial Differential Equations (PDEs)

Partial Differential Equations are equations that involve partial derivatives, which describe the rate of change of a quantity with respect to several variables. In the video, PDEs are the central theme, with a focus on solving them in the context of electrostatics using numerical methods. The script discusses Laplace's and Poisson's equations, which are types of PDEs fundamental to understanding potential fields.

💡Electrostatics

Electrostatics is a branch of physics that deals with the static electric charges at rest and the electric fields they produce. In the script, the concept of electrostatics is used as the physical context for solving PDEs, specifically Laplace's and Poisson's equations, to determine the potential and electric fields around charged objects.

💡Relaxation Technique

The relaxation technique is a numerical method used to solve PDEs by iteratively approximating the solution until it converges to the actual solution. The script introduces this technique as a fundamental approach to solving Laplace's and Poisson's equations on a lattice, highlighting its simplicity and the iterative process of refining the potential at each lattice point.

💡Lattice

In the context of the video, a lattice refers to a discrete grid used to approximate the solution of a continuous problem, such as a PDE. The script describes forming a two-dimensional lattice to discretize the problem space and solve for the potential at each lattice point, which is a key step in the numerical solution process.

💡Finite Differences

Finite differences are approximations of derivatives using discrete values. The script explains how derivatives in PDEs are expressed as finite differences on the lattice points, which simplifies the PDE into an algebraic equation that can be solved iteratively using the relaxation technique.

💡Taylor Series

The Taylor series is a mathematical representation used to approximate functions as the sum of terms calculated from the values of the function's derivatives at a single point. In the script, the Taylor series is used to derive an expression for the second derivative, which is key to formulating the finite difference approximation for the PDEs.

💡Jacobi Method

The Jacobi method is a specific iteration technique within the relaxation method, where the new values of the potential are calculated using the old values from surrounding points. The script mentions this method as a simple-minded approach that maintains the symmetry of boundary conditions but may not converge as quickly as other methods.

💡Gauss-Seidel Method

The Gauss-Seidel method is an improvement over the Jacobi method, where updated values of the potential are used immediately in subsequent calculations. The script describes this method as a way to potentially speed up the convergence of the iterative process by using the most current information available.

💡Successive Over-Relaxation (SOR)

Successive Over-Relaxation is an advanced iteration technique that aims to accelerate the convergence of the relaxation method by adjusting the amount of correction applied to the potential at each step. The script introduces SOR with a parameter omega, which can be tuned to find the best balance between speed and stability in the convergence process.

💡Boundary Conditions

Boundary conditions are constraints applied to the solution of a problem at its edges or limits. In the script, boundary conditions are essential for solving PDEs numerically, as they define the known potential values on the edges of the lattice, which the iterative process then uses to determine the interior solution.

💡Capacitor

A capacitor is a device that stores electrical energy in an electric field. The script discusses the application of the numerical methods to study realistic capacitors, including the effects of plate thickness and fringing fields, which are important considerations in electrostatics and electrical engineering.

💡Charge Density

Charge density refers to the amount of electric charge per unit volume or area. In the context of the script, once the potential is found by solving Laplace's or Poisson's equation, the charge density can be determined by taking the second derivative of the potential, providing insight into how charge accumulates on the surfaces of capacitors.

💡Electric Field

The electric field is a vector field that surrounds electric charges and exerts a force on other charges placed within the field. The script explains that the electric field can be derived from the gradient of the potential, and it discusses visualizing the electric field using numerical methods, such as plotting equipotential surfaces and field lines.

Highlights

Introduction to solving partial differential equations using relaxation techniques in electrostatics.

Explanation of Laplace's and Poisson's equations and their applications in two and three dimensions.

Discretization of continuous problems on a lattice for numerical solutions.

Use of finite differences to approximate derivatives in solving partial differential equations.

Introduction of the finite element method as an alternative to finite differences.

Technique of expressing derivatives as finite differences on lattice points for solving equations.

The concept of relaxation as an iterative method for solving partial differential equations.

Description of the Jacobi method for iterative solution of linear equations.

Introduction of the Gauss-Seidel method as an improvement over the Jacobi method.

Explanation of successive over-relaxation (SOR) as a further enhancement of the Gauss-Seidel method.

The importance of empirical determination of the relaxation parameter omega in SOR.

Practical implementation of relaxation techniques through the 'laplace line' program.

Investigation of realistic capacitors and the effects of fringing fields on electric potential.

Study of the potential and charge distribution in capacitors with thick plates.

Application of Poisson's equation to determine charge density from known potential.

Assessment of numerical solutions through surface plots and convergence checks.

Comparison of numerical solutions to analytical solutions using Fourier series.

Visualization of electric fields derived from potential surfaces using gradient calculations.

Encouragement to explore various geometries and boundary conditions for capacitors.

Final remarks on the practicality of relaxation techniques in solving real-world electric field problems.

Transcripts

Browse More Related Video

19.2 Electrostatic PDEs I

19. Intro Partial DIfferential Equations (PDEs)

Maxwell’s Equations Part 1: Gauss’s Law for the Electric Field

25. Computational Fluid Flow, Hydrodynamics

Wave Equation

(1 of 2) Electricity and Magnetism - Review of All Topics - AP Physics C

Related Tags

PDE Solutions Electrostatics Relaxation Method Laplace Equation Partial Differential Equations Numerical Methods Finite Differences Gauss-Seidel Successive Over-Relaxation Capacitor Modeling