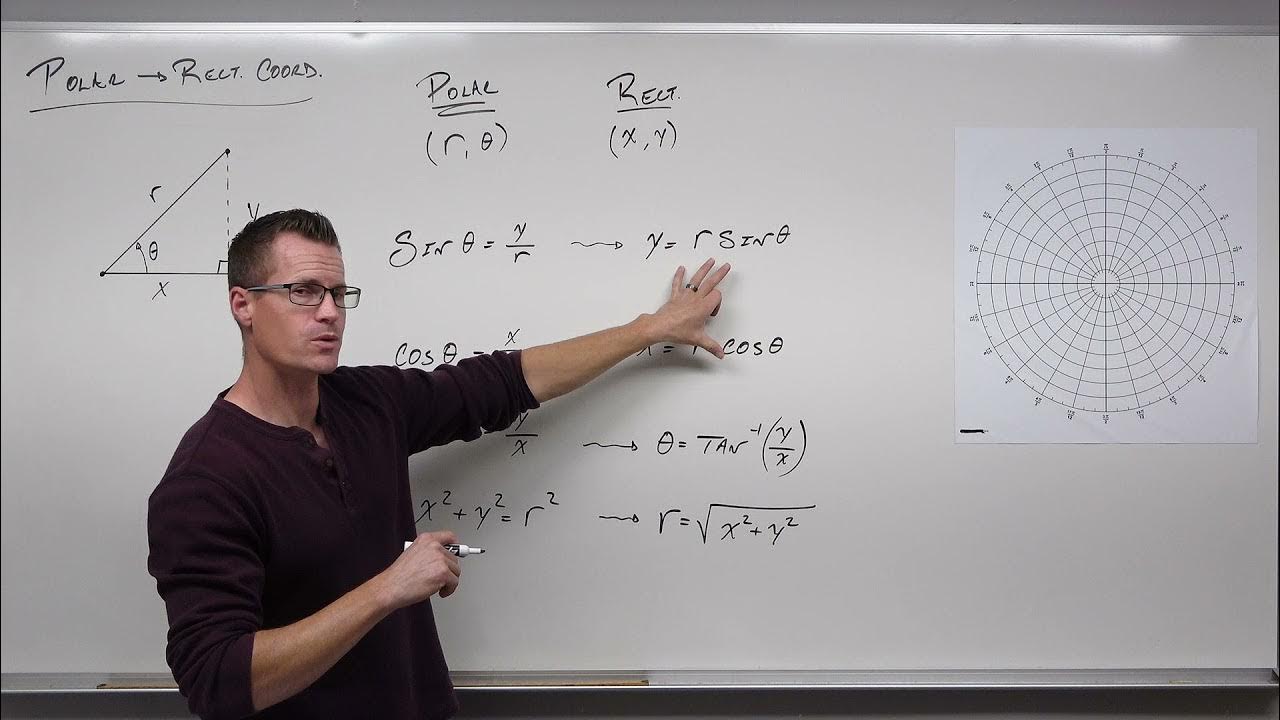Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Valu

The Organic Chemistry Tutor

17 May 201722:29

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video offers a comprehensive introduction to polar coordinates, contrasting them with rectangular coordinates. It explains how to plot polar coordinates by using radius (r) and angle (theta), demonstrating the process with various examples. The video also covers how to handle negative r values and convert between polar and rectangular coordinates using mathematical formulas. Additionally, it teaches how to find multiple polar coordinates that lead to the same point and how to derive r and theta from given rectangular coordinates, making it an informative resource for anyone looking to understand the basics of polar coordinate systems.

Takeaways

📚 The video provides a basic introduction to polar coordinates, explaining the difference between rectangular and polar coordinates.
📐 Polar coordinates are represented by r (radius) and θ (theta, the angle measured from the positive x-axis), while rectangular coordinates use x and y variables.
📈 To plot a point in polar coordinates, one must draw circles for different radii and a ray at the specified angle that intersects the appropriate circle.
🔢 The video demonstrates how to plot points like 3,45° and 2,3π/4 by converting angles to degrees and understanding the quadrants.
🤔 It explains that a negative radius involves plotting the point in the opposite direction by adding 180 degrees to the angle.
🔄 The script clarifies that multiple polar coordinate pairs can represent the same point, with variations in the sign of r and θ.
🔢 The conversion from polar to rectangular coordinates is done using x = r*cos(θ) and y = r*sin(θ).
🔄 Similarly, converting from rectangular to polar coordinates involves calculating r as the square root of x^2 + y^2 and θ using the arctangent function.
🧭 The importance of considering the quadrant in which the point lies when converting from rectangular to polar coordinates is emphasized.
📝 The video script includes examples and exercises to help viewers understand the process of plotting and converting between coordinate systems.

Q & A

What is the main difference between rectangular and polar coordinates?
-Rectangular coordinates consist of x and y variables, while polar coordinates consist of r (radius) and theta (angle measured from the positive x-axis).
How do you plot a point with polar coordinates (r, theta)?
-First, plot circles with various radii. Then, draw a ray at the angle theta from the positive x-axis and extend it to the circle with radius r.
What is the significance of plotting circles with different radii when graphing polar coordinates?
-Plotting circles with different radii helps to determine the location on the graph corresponding to the radius r in a polar coordinate.
How do you convert an angle from radians to degrees?
-To convert radians to degrees, multiply the radian value by 180 and divide by pi (π).
What is the effect of a negative radius (r) in polar coordinates?
-A negative radius in polar coordinates means that you should travel 180 degrees in the opposite direction from where you would normally go for a positive radius.
How can you find the other three polar coordinates that lead to the same terminal point given one polar coordinate (r, theta)?
-The other three polar coordinates are (r, -theta), (-r, theta + 180°), and (-r, -theta - 180°), considering the angle theta is between -360° and 360°.
What is the formula to convert polar coordinates (r, theta) to rectangular coordinates (x, y)?
-The formulas are x = r * cos(theta) and y = r * sin(theta).
How do you find the radius (r) and angle (theta) from rectangular coordinates (x, y)?
-The radius r is the square root of (x^2 + y^2), and the angle theta is the arctangent of (y/x), considering the quadrant to adjust for the correct direction.
What is the meaning of the term 'terminal point' in the context of polar coordinates?
-The 'terminal point' in polar coordinates refers to the final location on the graph where the radius r and angle theta intersect.
Can you provide an example of converting rectangular coordinates to polar coordinates?
-For the rectangular coordinates (-5, 5√3), the radius r is √((-5)^2 + (5√3)^2) = √(25 + 75) = √100 = 10. The angle theta is the arctangent of (5√3 / -5) with adjustments for quadrant II, which gives us an angle of 180° - 60° = 120°. Thus, the polar coordinates are (10, 120°) or (10, 2π/3 radians).

Outlines

00:00

📚 Introduction to Polar Coordinates

This paragraph introduces the concept of polar coordinates, contrasting them with the more familiar rectangular coordinates. Rectangular coordinates are defined by x and y variables, while polar coordinates are represented by r (radius) and θ (theta, the angle from the positive x-axis). The paragraph explains how to plot a point in polar coordinates, using the example of (3, 45°), by drawing circles for different radii and a ray at the specified angle. It also covers how to convert an angle from radians to degrees and vice versa, and discusses the implications of a negative radius, which involves plotting in the opposite direction and adding 180 degrees to the angle.

05:01

📐 Plotting Points with Polar Coordinates

The second paragraph delves deeper into plotting points in polar coordinates, specifically addressing how to handle points with angles in different quadrants and negative radii. It explains the process of plotting points like (2, 135°) and (-2, 60°), emphasizing the conversion of radians to degrees for clarity. The paragraph also explores alternative representations of a point, such as negative coordinates leading to the same location on the graph, and how to find additional polar coordinates that result in the same terminal point, considering the restrictions on the angle θ.

10:02

🔍 Finding Multiple Polar Coordinates for a Single Point

This paragraph continues the discussion on polar coordinates by illustrating how to find multiple sets of polar coordinates that correspond to the same location on the graph. It provides a step-by-step method to determine these coordinates, starting with a given point like (2, 30°) and calculating the other three points that share the same terminal point. The process involves adjusting the angle by subtracting or adding 360° and 180°, and considering both positive and negative r values. The explanation includes plotting these points and understanding the geometric implications of these adjustments.

15:03

📉 Conversion Between Polar and Rectangular Coordinates

The fourth paragraph focuses on the mathematical conversion between polar and rectangular coordinates. It explains the formulas to convert a polar coordinate (r, θ) into a rectangular coordinate (x, y), where x = r * cos(θ) and y = r * sin(θ). The paragraph provides examples, such as converting (4, 60°) and (6, 5π/6) into their rectangular equivalents, demonstrating the calculations involved in finding the x and y values based on the given r and θ.

20:05

📚 Conversion from Rectangular to Polar Coordinates

The final paragraph discusses the reverse process of converting rectangular coordinates into polar coordinates. It outlines the method to determine the radius r, which is the square root of the sum of the squares of x and y, and the angle θ, which is found using the arctangent of y divided by x. The paragraph includes examples, such as converting the points (2, -4) and (-5, 5√3) into polar form, detailing the steps to calculate r and θ, and adjusting for the correct quadrant to find the final polar coordinates.

Mindmap

Keywords

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system where each point on a plane is determined by a distance from a reference point and an angle from a reference direction. In the video, polar coordinates are introduced as an alternative to the more commonly known rectangular coordinates, with the script explaining that polar coordinates consist of a radius (r) and an angle (theta), which is measured from the positive x-axis.

💡Rectangular Coordinates

Rectangular coordinates, also known as Cartesian coordinates, are a system where each point is defined by two perpendicular distances, typically x and y, from two intersecting lines called axes. The script contrasts rectangular coordinates with polar coordinates, emphasizing that while rectangular coordinates use x and y variables, polar coordinates use r and theta.

💡Radius (r)

The radius, denoted as 'r' in polar coordinates, represents the distance from the origin (reference point) to the point in question. The script uses the radius to illustrate how to plot points in polar coordinates, such as plotting a point with a radius of 3 units.

💡Theta (θ)

Theta, represented by the symbol 'θ', is the angle in polar coordinates measured from the positive x-axis. The video script explains how theta is used in conjunction with the radius to plot points and provides examples of plotting points with different theta values, such as 45 degrees and 135 degrees.

💡Graphing

Graphing in the context of the video refers to the process of visually plotting and representing data points on a graph. The script discusses how to graph polar coordinates by drawing circles for different radii and rays for different angles to represent points like '3, 45 degrees' and '2, 135 degrees'.

💡Negative Radius

A negative radius in polar coordinates indicates a point that is located in the opposite direction of the positive radius but at the same distance from the origin. The video script explains how to plot points with a negative radius, such as '-2, 60 degrees', by traveling in the opposite direction of where the positive radius would lead.

💡Conversion to Degrees

The script mentions the conversion of angles from radians to degrees to better understand their position on the coordinate system. For instance, '3 pi over 4' is converted to degrees by multiplying by '180/pi', resulting in 135 degrees, which helps in plotting the point (2, 135 degrees) on the graph.

💡Quadrants

Quadrants refer to the four equal areas formed by the intersection of the x and y axes in the coordinate plane. The script uses the concept of quadrants to explain the location of points with different angles, such as how 135 degrees places a point in quadrant two.

💡Conversion to Rectangular Coordinates

The video script explains the process of converting polar coordinates to rectangular coordinates using the formulas x = r * cos(theta) and y = r * sin(theta). An example given is converting the polar coordinate '4, 60 degrees' to rectangular coordinates, resulting in x = 2 and y = 2 root 3.

💡Arc Tangent (arctan)

Arc tangent, often abbreviated as arctan or tan^-1, is a trigonometric function that is used to find the angle whose tangent is a given number. In the script, arctan is used to determine the angle theta when converting rectangular coordinates to polar coordinates, such as finding the angle for the point (2, -4).

💡Reference Angle

A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. The script discusses finding the reference angle when determining the angle theta for polar coordinates, such as using the arctan of 4/2 to find a reference angle of 63.4 degrees before adjusting for the correct quadrant.

Highlights

Introduction to polar coordinates and their difference from rectangular coordinates.

Explanation of polar coordinates consisting of radius 'r' and angle 'theta'.

Step-by-step guide on plotting polar coordinates, such as (3, 45 degrees).

Demonstration of plotting multiple circles for different radii.

Conversion of angle from radians to degrees for plotting.

Plotting a point with a negative radius and its implications.

Understanding the effect of a negative radius on the direction of plotting.

Finding alternative polar coordinates for a given point.

Method to determine four different polar coordinates for the same terminal point.

Conversion of polar coordinates to rectangular coordinates using formulas.

Example of converting a polar coordinate (4, 60 degrees) to rectangular form.

Explanation of converting rectangular coordinates to polar form.

Calculation of radius 'r' from rectangular coordinates.

Determination of angle 'theta' using arctangent and quadrant considerations.

Conversion of a point (-5, 5√3) into polar coordinates with example.

Conversion of angle measurements from degrees to radians.

Summary of the process to find four polar points given one point.

Practical application of understanding polar and rectangular coordinate systems.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 9.7

Lesson 14 - Polar Equations (Calculus 2 Tutor)

How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar Curves

Introduction to Polar Coordinates (Precalculus - Trigonometry 36)

Double Integrals in Polar Coordinates

Related Tags

Polar Coordinates Graphing Rectangular Coordinates Coordinate Conversion Radians Degrees Trigonometry Mathematics Tutorial Educational Content Geometry Calculus