Definition of the Derivative
TLDRThis video delves into the concept of the instantaneous rate of change and the definition of a derivative in calculus. It explains the difference between the average rate of change and the instantaneous rate, highlighting the secant and tangent lines' roles. The presenter illustrates how to find the slope of the tangent line using limits and introduces derivative notation, f'(x) and dy/dx. The script also covers the conditions for a function to be differentiable, the relationship between differentiability and continuity, and provides examples of derivative calculations and interpretations.
Takeaways
- 📚 The video discusses the concept of the instantaneous rate of change and the definition of a derivative, contrasting it with the previously discussed average rate of change.
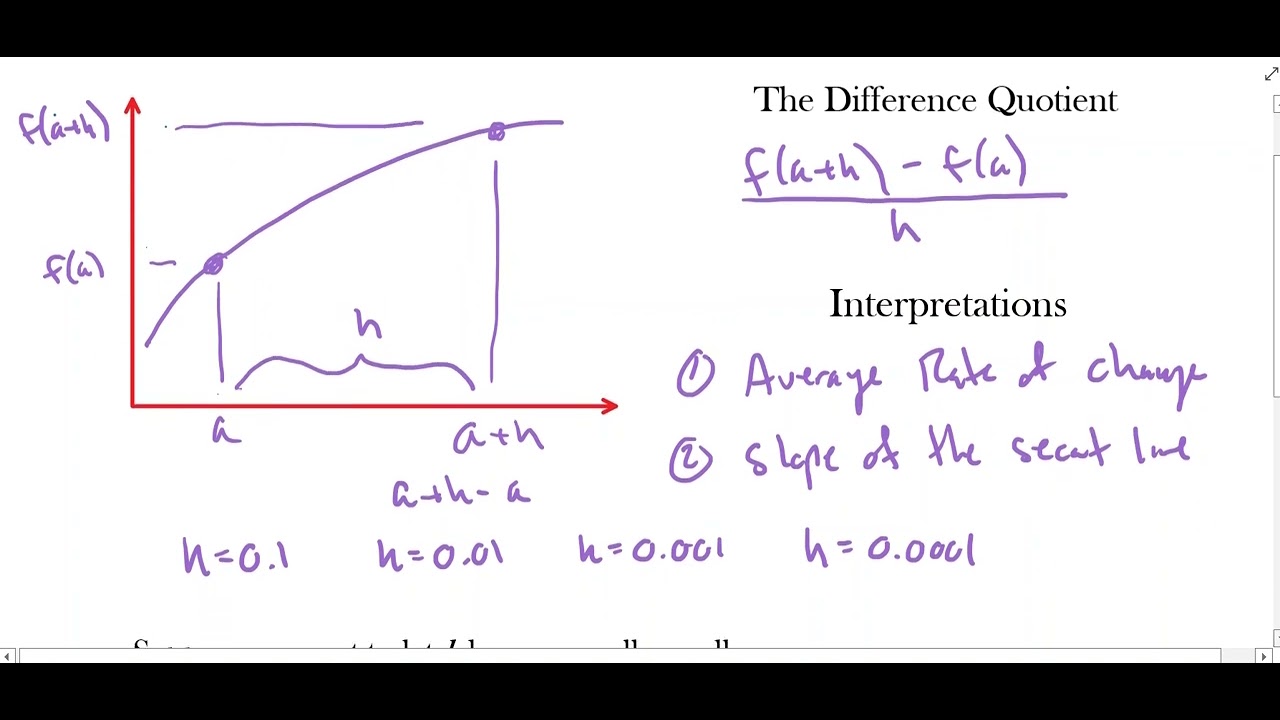
- 📉 The average rate of change is likened to the slope of a secant line between two points on a graph, while the instantaneous rate of change is the slope of the tangent line at a specific point.
- 🔍 The behavior of a function at a specific point x=a can be better understood by examining the slope of the tangent line at that point, which captures the function's trajectory at that exact moment.
- 🤔 The slope of the tangent line is approached by moving the secant line's second point, b, closer and closer to the point of interest, a, until the limit of 'rise over run' as the 'run' approaches zero is found.
- 📝 The instantaneous rate of change of a function f at a point x=c is mathematically defined as the limit \(\lim_{h \to 0} \frac{f(c+h) - f(c)}{h}\).
- 📈 The derivative of a function is represented by \( f'(c) \) or \( \frac{dy}{dx} \) at x=c and signifies the slope of the tangent line to the graph of the function at that point.
- 📉 The derivative of a function can be thought of as a function itself, \( f'(x) \), which gives the slope of the tangent line at any x value.
- 🚫 A function is not differentiable at points where the derivative does not exist, such as at sharp corners, vertical tangents, or discontinuities.
- 🔄 Differentiability implies continuity; if a function is differentiable at a point, it is also continuous at that point, though the converse is not necessarily true.
- 📝 The derivative can be computed using the limit definition, but in practice, derivative rules are typically applied for efficiency rather than directly computing limits.
- 📈 The graph of the derivative of a function provides insight into where the original function has a horizontal tangent (derivative is zero), and the intervals of increasing and decreasing slopes.
Q & A
What is the instantaneous rate of change of a function?
-The instantaneous rate of change of a function is the slope of the tangent line to the graph of the function at a specific point. It is defined as the limit of the average rate of change as the interval between two points approaches zero.
How is the average rate of change different from the instantaneous rate of change?
-The average rate of change is the slope of the secant line between two points on the graph of a function, representing the behavior of the function over a closed interval. In contrast, the instantaneous rate of change focuses on the behavior of the function at a single point, using the slope of the tangent line at that point.
What is the definition of the derivative?
-The derivative of a function at a point is the instantaneous rate of change of the function at that point. It is mathematically defined as the limit of (f(c+h) - f(c)) / h as h approaches zero.
Why is the derivative important in understanding the behavior of a function?
-The derivative provides information about the slope of the tangent line to the graph of a function at any given point, which helps in understanding the rate at which the function is increasing or decreasing at that point. It is crucial for analyzing the function's behavior, such as finding local maxima, minima, and points of inflection.
What is the difference between a secant line and a tangent line in the context of a function graph?
-A secant line connects two points on the graph of a function, representing the average rate of change over an interval. A tangent line, on the other hand, touches the graph at exactly one point (the point of tangency) and represents the instantaneous rate of change at that point.
What does it mean for a function to be differentiable at a point?
-A function is differentiable at a point if the limit of the difference quotient exists at that point. This means that the instantaneous rate of change, or the derivative, is well-defined and exists at that specific point on the graph.
How is the derivative related to the continuity of a function?
-If a function is differentiable at a point, it is also continuous at that point. Differentiability implies that the function has a well-defined limit at that point, which is a requirement for continuity. However, continuity does not necessarily imply differentiability, as a function can be continuous at a point where it is not differentiable (e.g., at a sharp corner or a vertical tangent).
What is the geometric interpretation of the derivative?
-The geometric interpretation of the derivative is the slope of the tangent line to the graph of a function at a given point. It provides a measure of how steep the graph is at that point and indicates the direction of the greatest rate of increase or decrease of the function.
What are some common notations used for the derivative?
-Common notations for the derivative include f'(x), which represents the derivative of the function f at x, and dy/dx, which is used when the function is expressed as y = f(x). Both notations indicate the rate of change of y with respect to x.
How can you determine the equation of the tangent line to a function at a specific point?
-To determine the equation of the tangent line to a function at a specific point, you need the slope of the tangent line (which is the derivative at that point) and a point through which the tangent line passes (the point of tangency). Using the point-slope form of a line equation, you can then write the equation of the tangent line.
Outlines
📈 Introduction to Instantaneous Rate of Change and Derivatives
The video begins by introducing the concept of the instantaneous rate of change and the definition of a derivative. It contrasts this with the previously discussed average rate of change, highlighting the difference between the slope of a secant line and the slope of a tangent line at a specific point on a graph. The presenter explains the process of finding the slope of the tangent line by taking the limit of the rise over run as the run approaches zero, and introduces the algebraic notation for this concept. They also provide an example using the function f(x) = x - 2 squared to illustrate the calculation of the instantaneous rate of change.
🔍 Examples of Derivatives and Tangent Line Slopes
This paragraph provides examples of how to calculate derivatives and the slopes of tangent lines for given functions. It explains that the instantaneous rate of change at a specific point can be found by evaluating the limit of the difference quotient. The presenter uses the functions f(x) = x - 2 squared and g(x) = 4x - 3 to demonstrate how to find the slope of the tangent line at particular points, emphasizing that the slope of a tangent line to a function at a given point is the derivative at that point.
📚 Derivative Notation and the Concept of Differentiability
The presenter introduces derivative notation, explaining the use of f'(c) and dy/dx to represent the instantaneous rate of change or the slope of the tangent line at a given point x = c. They define the term 'differentiable,' stating that a function is differentiable at a point if the limit that defines the derivative exists. The paragraph also discusses scenarios where a function may not be differentiable, such as at sharp corners, vertical tangents, or points of discontinuity, and clarifies that differentiability implies continuity but not vice versa.
📉 Continuity and Differentiability Relationship
This section delves into the relationship between continuity and differentiability. It asserts that if a function is differentiable at a point, it must also be continuous at that point, though the converse is not true. The presenter provides a proof for this theorem, using the definition of differentiability and continuity to show that if a function has a derivative at a point, the limit of the function as x approaches that point is equal to the function's value at that point, thus proving continuity.
📚 Derivative Rules and Graphical Interpretation
The video script discusses basic derivative rules, such as the derivative of a linear function and the derivative of a constant. It also introduces the concept of sketching the graph of a function's derivative based on the function's graph, identifying points where the tangent line is horizontal and intervals where the slope of the tangent is positive or negative. The presenter guides the viewer through the process of sketching the derivative graph from the original function's graph and vice versa.
📘 Derivative Computation and Tangent Line Equations
The paragraph demonstrates how to compute derivatives using the limit definition, showcasing the process with a specific function and emphasizing that while this method is theoretically important, it is not commonly used in practice due to the availability of derivative rules. It also explains how to find the equation of a tangent line to a graph at a given point, using the slope from the derivative and the point of tangency from the original function.
📌 Understanding Function Notations and Tangency
In the final paragraph, the presenter clarifies the meaning of function notations, specifically h'(1) and h(1), in the context of finding the slope of the tangent line and the y-value of the function at x = 1. They illustrate how to determine that the tangent line has the same slope and y-value as the function at the point of tangency, reinforcing the concept of tangency with a practical example.
Mindmap
Keywords
💡Instantaneous Rate of Change
💡Derivative
💡Average Rate of Change
💡Secant Line
💡Tangent Line
💡Limit
💡Differentiable
💡Continuity
💡Sharp Corner
💡Vertical Tangent
💡Discontinuity
Highlights
Introduction to the concept of instantaneous rate of change and the definition of a derivative.
Explanation of the difference between average rate of change and instantaneous rate of change.
Visual representation of how the slope of a secant line approximates the slope of a tangent line as points get closer.
The mathematical definition of the instantaneous rate of change using the limit as the change in the independent variable approaches zero.
Algebraic representation of the derivative formula and its interpretation.
Illustration of how to find the slope of the tangent line at a specific point on a graph.
Examples of calculating derivatives for simple functions to demonstrate the concept.
Introduction of notation for derivatives, including f'(c) and dy/dx.
Definition of the term 'differentiable' and conditions under which a function is considered differentiable.
Explanation of scenarios where a function may not be differentiable, such as sharp corners, vertical tangents, and discontinuities.
The relationship between differentiability and continuity, and the proof that differentiability implies continuity.
Derivation of basic derivative rules for linear functions and constants.
Demonstration of sketching the graph of a function's derivative based on the original function's graph.
Method for sketching the graph of a function from its derivative, including identifying intervals of increasing and decreasing slopes.
Approach to finding the derivative of a function involving an absolute value by graphical analysis.
Computational method for finding the derivative using the limit definition, demonstrated with an example.
How to determine the equation of a tangent line to a graph at a given point using the derivative.
Final example illustrating the meaning of function notation and the concept of a tangent line in the context of a function and its derivative.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: