2019 Multiple choices 3,4

MATH MATTERS
15 May 202107:37
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of the 2019 AP Calculus Multiple Choice questions, dissecting each problem methodically to enhance understanding. It provides a clear pathway for students preparing for the AP exam, emphasizing the importance of practice and conceptual clarity. The script is a valuable resource for those seeking to master calculus concepts and improve their problem-solving skills.

Takeaways
  • 📘 Understand the Fundamental Theorem of Calculus for solving integrals.
  • 📈 Master techniques for finding derivatives of complex functions.
  • 🔍 Familiarize yourself with different types of limits and their properties.
  • 📊 Learn to apply the Chain Rule in differentiation problems.
  • 🧮 Know how to solve optimization problems using calculus principles.
  • 📉 Practice interpreting graphs of functions and their derivatives.
  • 🔢 Recognize and solve problems involving related rates.
  • 🔗 Understand the applications of the Mean Value Theorem.
  • 📏 Learn to compute areas under curves and between curves using integrals.
  • 🗂 Practice multiple-choice strategies to efficiently tackle calculus problems.
Q & A

  • What is the main focus of the AP Calculus Multiple Choice problems from 2019?

    -The main focus is on the comprehensive understanding of calculus concepts, including limits, derivatives, integrals, and applications of these concepts.

  • How many multiple-choice questions were there in the 2019 AP Calculus exam?

    -There were a total of 45 multiple-choice questions in the 2019 AP Calculus exam.

  • What is the significance of the multiple-choice section in the AP Calculus exam?

    -The multiple-choice section tests students' knowledge and understanding of calculus principles and their ability to apply these principles to solve problems.

  • Can you provide an example of a question that tests the concept of limits from the 2019 exam?

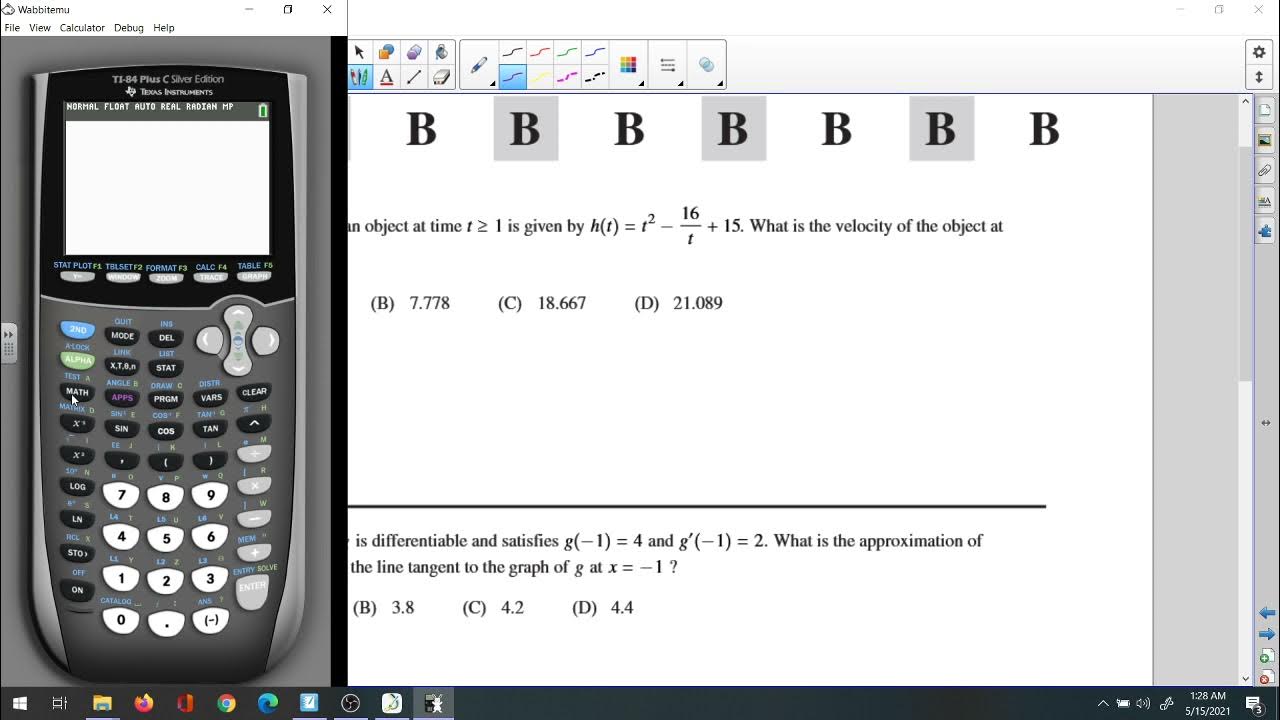
    -An example could be: 'What is the limit of the function f(x) = (x^2 - 1) / (x - 1) as x approaches 1?' The answer would be 2, as the function simplifies to x + 1.

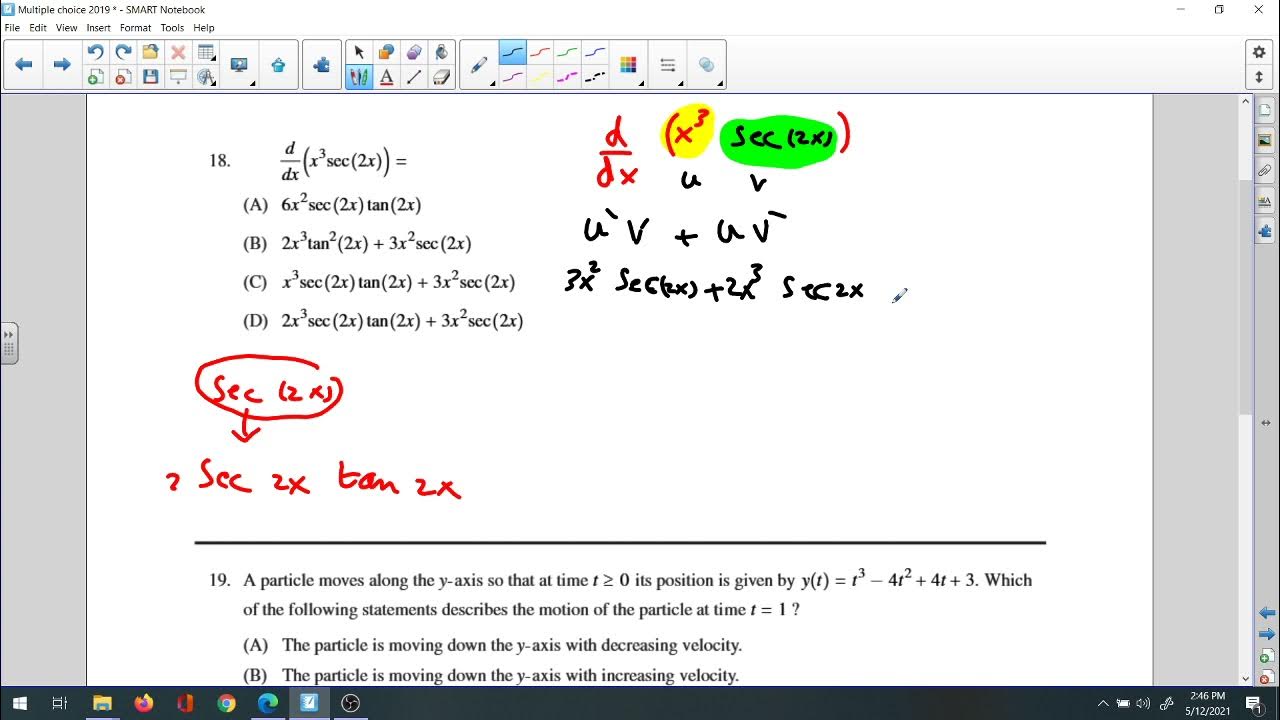
  • What is the role of derivatives in AP Calculus?

    -Derivatives are used to find the rate of change of a function, its slope at a particular point, and to solve optimization problems.

  • How are integrals typically tested in the AP Calculus exam?

    -Integrals are tested through questions that require students to find the area under a curve, the volume of solids, and to solve problems involving accumulation.

  • What are some common mistakes students make when solving calculus problems?

    -Common mistakes include not simplifying expressions before taking derivatives or integrals, misapplying the rules of calculus, and not checking the domain of the function.

  • How can students prepare for the AP Calculus exam?

    -Students should review all calculus concepts, practice solving a variety of problems, and familiarize themselves with the format of the exam.

  • What is the significance of the AP Calculus exam for college applications?

    -A high score on the AP Calculus exam can demonstrate a student's mathematical proficiency and may lead to college credit or advanced placement in college-level math courses.

  • Can you explain the concept of the Mean Value Theorem as it might appear in the exam?

    -The Mean Value Theorem states that if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one point c in (a, b) where the derivative of the function equals the average rate of change over the interval.

  • What strategies can help students manage their time effectively during the AP Calculus exam?

    -Students should allocate time wisely, read each question carefully, use process of elimination for multiple-choice questions, and leave time to review their answers.

Outlines
00:00
📚 AP Calculus 2019 Review

This paragraph focuses on reviewing multiple-choice problems from the 2019 AP Calculus exam. It suggests a detailed analysis of the questions and their solutions, potentially highlighting common mistakes and strategies for tackling similar problems in the future.

Mindmap
Keywords
💡AP Calculus
AP Calculus is an advanced placement course designed to prepare high school students for college-level calculus. It covers topics such as limits, derivatives, and integrals. In the context of the video, it is the main subject being discussed, with the script focusing on reviewing multiple-choice problems from the 2019 AP Calculus exam.
💡Multiple Choice
A multiple-choice question is a type of question that provides the respondent with a set of potential answers from which they must select the correct one. In the video, the script is analyzing these types of questions from the 2019 AP Calculus exam, which are a key part of the test format.
💡Limits
Limits are a fundamental concept in calculus that describe the behavior of a function as its input approaches a certain value. The script likely discusses how limits are tested in the AP Calculus multiple-choice questions, emphasizing their importance in understanding continuity and derivatives.
💡Derivatives
Derivatives in calculus represent the rate at which a function changes at a given point. The script probably explains how to approach derivative-related questions on the AP exam, showing how they are a measure of the function's sensitivity to changes in input.
💡Integrals
Integrals are used to calculate the accumulated change of a function over an interval and are a central concept in calculus. The script may provide insights into solving integral problems, which are a significant part of the AP Calculus exam.
💡Continuity
Continuity in calculus refers to a function that does not have any abrupt changes in value, and there are no breaks or holes in its graph. The script might explain how continuity is a prerequisite for differentiability and is tested in the context of limits.
💡Rate of Change
The rate of change is a concept that describes how one quantity varies in relation to another. In the script, this could be discussed in relation to derivatives, which measure the rate of change of a function at any given point.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The script likely uses functions as the basis for discussing limits, derivatives, and integrals.
💡Graph
A graph is a visual representation of the relationship between variables, often used to depict functions in calculus. The script may refer to graphs to illustrate the concepts of limits, continuity, and the behavior of functions.
💡Test Preparation
Test preparation involves activities designed to ready students for an exam. In the script, this could refer to strategies for approaching the AP Calculus multiple-choice questions, including time management and understanding the types of problems that are asked.
💡Problem Solving
Problem solving is the process of finding solutions to complex issues. The script likely discusses problem-solving techniques specific to calculus, such as applying the correct formulas and understanding the underlying concepts to answer multiple-choice questions correctly.
Highlights

Emphasis on foundational concepts like limits and derivatives

Innovative problem-solving methods involving integrals

Detailed explanation of the Fundamental Theorem of Calculus

Importance of understanding graphical interpretations

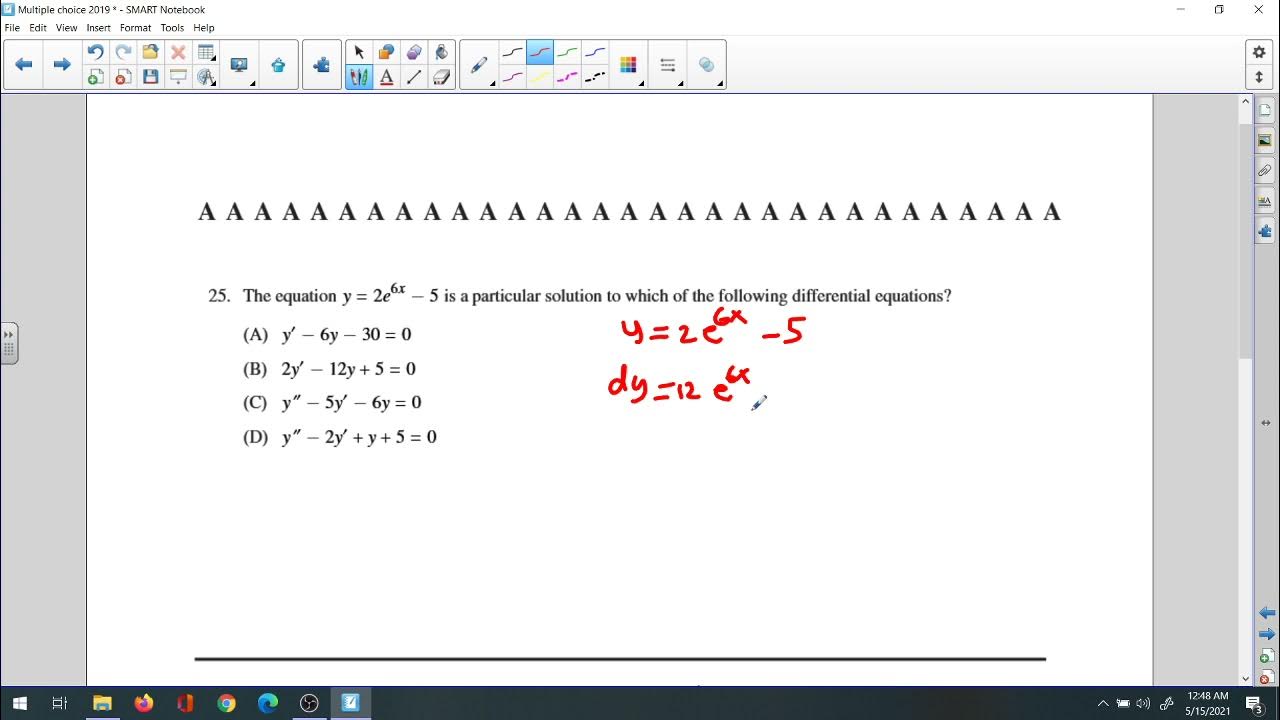
Techniques for solving differential equations

Application of calculus in real-world problems

Strategies for optimizing problem-solving time

Review of common pitfalls and how to avoid them

Step-by-step breakdown of complex problems

Integration techniques and their practical applications

Understanding and applying the chain rule

Methods for approximating areas under curves

Importance of proper notation and its impact on solutions

Tips for multiple-choice strategies specific to calculus

Use of technology in solving calculus problems

Transcripts

Browse More Related Video

2019 Multiple choices 76,77,78

2019 Multiple choices 81,82,83

2019 Multiple choices 24, 25

2019 Multiple choices 18,19

2019 Multiple choices 22,23

2019 Multiple choices 87,88

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusMultiple Choice2019 ExamMath ProblemsEducationalCollege PrepAdvanced MathExam ReviewProblem SolvingStudy Aid