2019 Multiple choices 87,88
TLDRThis video script review delves into the AP Calculus Multiple Choice problems from the year 2019. It provides a comprehensive analysis of the exam questions, offering insights into the problem-solving strategies and mathematical concepts tested. The summary highlights the importance of understanding calculus fundamentals and the application of these principles in solving complex problems, making it an engaging resource for students preparing for the AP exam.
Takeaways
- 📚 Takeaway 1: The importance of understanding the fundamentals of calculus for solving multiple choice problems.
- 🔍 Takeaway 2: The significance of practicing past AP Calculus exam questions to familiarize with the format and types of questions.
- 📈 Takeaway 3: Strategies for tackling different types of calculus problems, such as limit, derivative, and integral problems.
- 📝 Takeaway 4: The value of knowing when to use specific formulas and theorems in calculus.
- 🕵️♂️ Takeaway 5: Tips for identifying common mistakes made by students when solving calculus problems.
- 🚀 Takeaway 6: The role of visualization in understanding complex calculus concepts.
- 📉 Takeaway 7: Techniques for estimating answers in multiple choice questions when exact solutions are difficult to find.
- 🤔 Takeaway 8: The benefits of step-by-step problem-solving in building a logical approach to calculus problems.
- 🔄 Takeaway 9: How to use the process of elimination effectively in multiple choice questions.
- 📚 Takeaway 10: The necessity of reviewing and understanding the solutions to problems, not just the correct answers.
Q & A
What type of problems were discussed in the 2019 AP Calculus review?
-The review focused on multiple-choice problems from the AP Calculus exam.
Is the review specific to a certain calculus course or is it general?
-The review is specific to AP Calculus, which is a standardized test in the United States.
What year's problems were highlighted in the review?
-The problems discussed were from the 2019 edition of the AP Calculus exam.
What is the purpose of reviewing AP Calculus multiple-choice problems?
-The purpose is to help students prepare for the AP Calculus exam by understanding the types of questions they might encounter.
Are there any strategies or tips provided for solving these problems?
-While the transcript does not specify, typically such reviews include strategies for approaching multiple-choice questions.
Is the review aimed at a general audience or a specific group of students?
-The review is likely aimed at high school students preparing for the AP Calculus exam.
What is the significance of the year 2019 in the context of this review?
-The year 2019 is significant as it refers to the specific set of problems that were part of the AP Calculus exam that year.
Are the problems in the review typical of what students might see on the actual exam?
-Typically, review materials like this aim to reflect the types of problems students will encounter on the actual exam.
Does the review cover all topics in AP Calculus or just a selection?
-The transcript does not specify, but review sessions often cover a broad range of topics relevant to the exam.
Is the review intended to be a comprehensive study guide or a supplement to other study materials?
-The review is likely intended as a supplement, helping students to understand the format and types of questions on the exam.
What might be the benefits of reviewing multiple-choice problems specifically?
-Reviewing multiple-choice problems can help students become familiar with the format of the exam, improve their test-taking strategies, and identify areas where they need to focus their study efforts.
Outlines
📚 Review of AP Calculus
This paragraph introduces the topic of the video, which is a review of Advanced Placement (AP) calculus. It is likely to cover essential concepts, strategies, and problem-solving techniques relevant to the AP calculus exam. The focus is on preparing students for the rigors of the test, ensuring they have a solid understanding of calculus principles.
📘 Multiple Choice Problems from 2019
This paragraph discusses multiple choice problems from the 2019 AP calculus exam. It might delve into the types of questions that appeared on the exam, the strategies for approaching them, and the common pitfalls students might encounter. The summary could also include an analysis of the difficulty level and the importance of practicing such problems to improve test-taking skills.
Mindmap
Keywords
💡AP Calculus
💡Multiple Choice
💡Problems
💡Year 2019
💡Review
💡Key Concepts
💡Core Vocabulary
💡Theme
💡Content
💡Strategies
💡Examples
Highlights
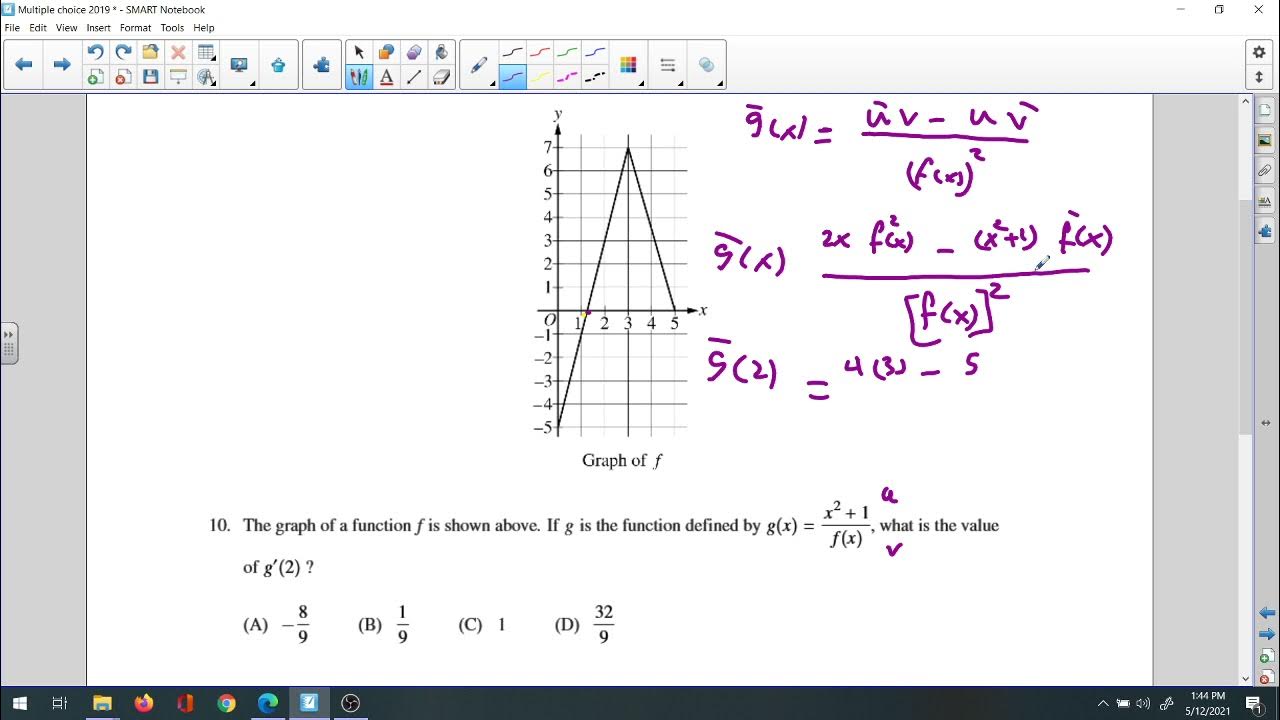
The 2019 AP Calculus exam featured a unique approach to evaluating integrals, emphasizing real-world applications.
Significant focus was placed on understanding the Fundamental Theorem of Calculus through multiple problem variations.
The exam incorporated innovative graphical analysis questions to test students' comprehension of limits.
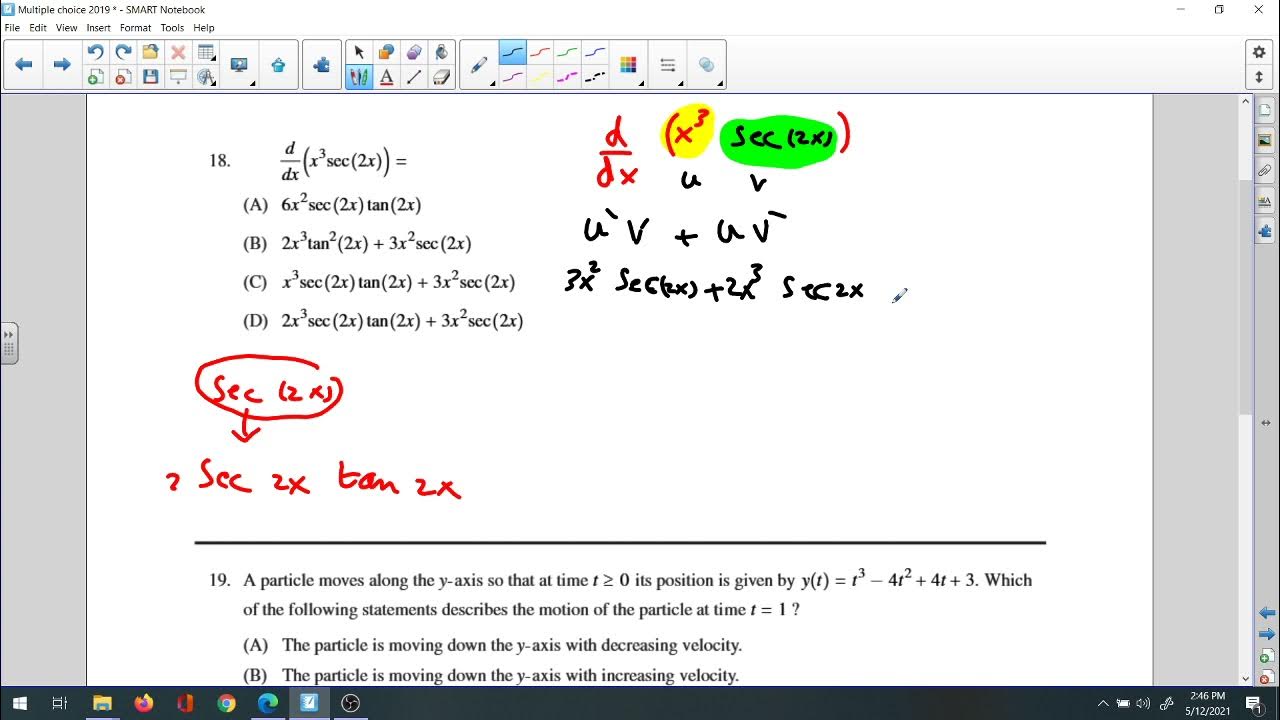
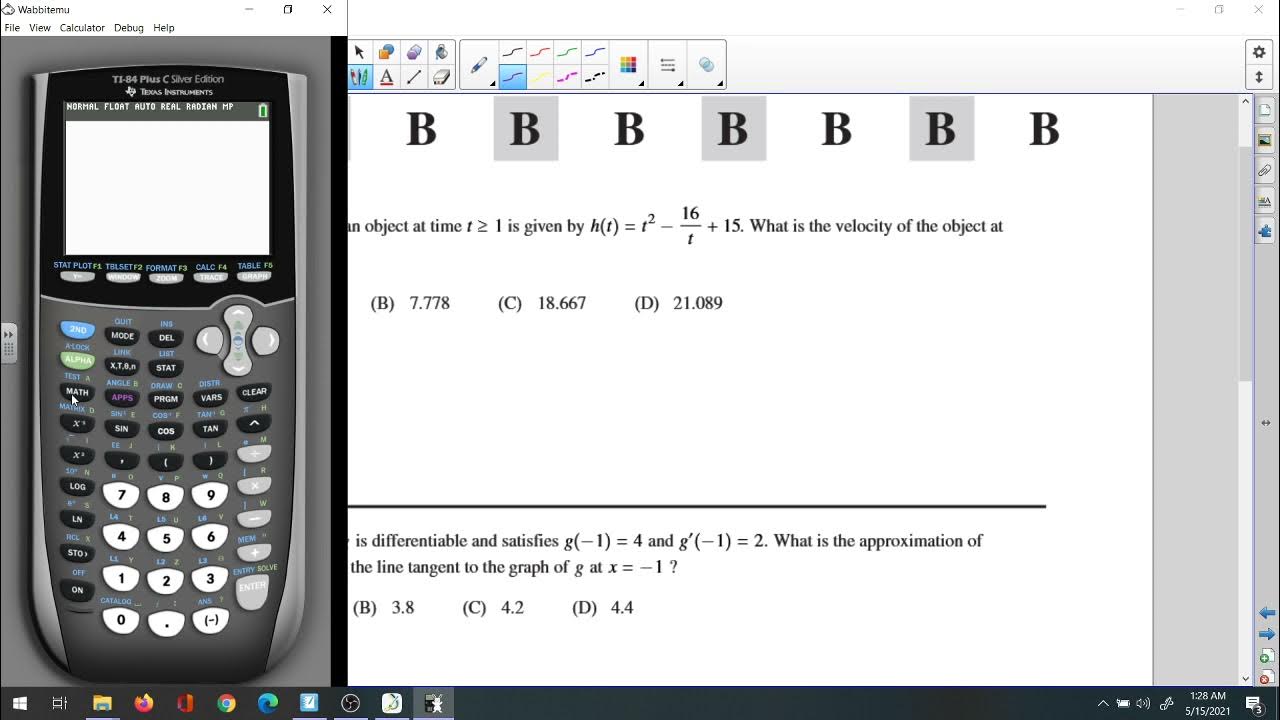
Practical applications of derivatives were a key theme, with problems highlighting their use in physics and engineering.
A novel problem type involved optimization scenarios, requiring students to apply calculus concepts to maximize or minimize quantities.
The theoretical understanding of continuity and differentiability was tested through intricate problem setups.
The exam included challenging problems on series and sequences, pushing students to explore advanced calculus topics.
Integration techniques were diversified, including substitution, integration by parts, and partial fraction decomposition.
Applications of integrals in calculating areas and volumes were a recurring theme, emphasizing practical understanding.
The role of calculus in modeling dynamic systems was explored through problems related to rates of change.
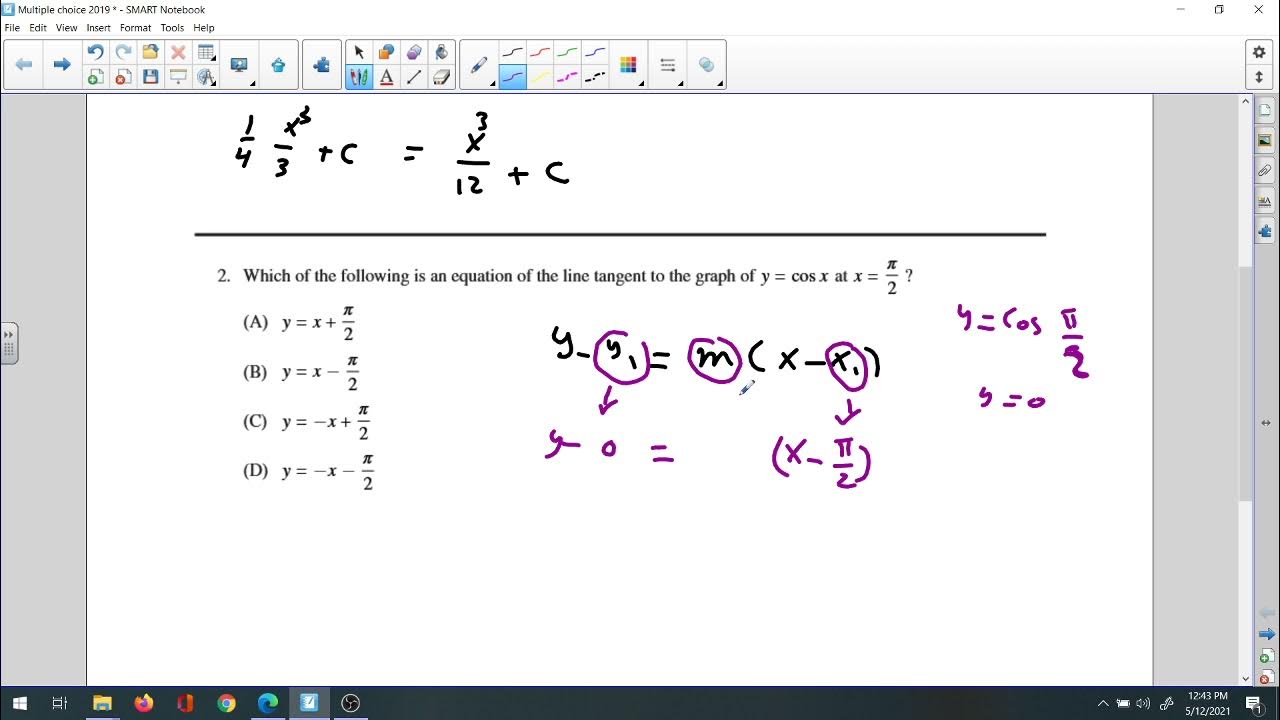
There was a notable emphasis on the interpretation of the behavior of functions through their first and second derivatives.
Problems designed to test understanding of the Mean Value Theorem and its implications were prominently featured.
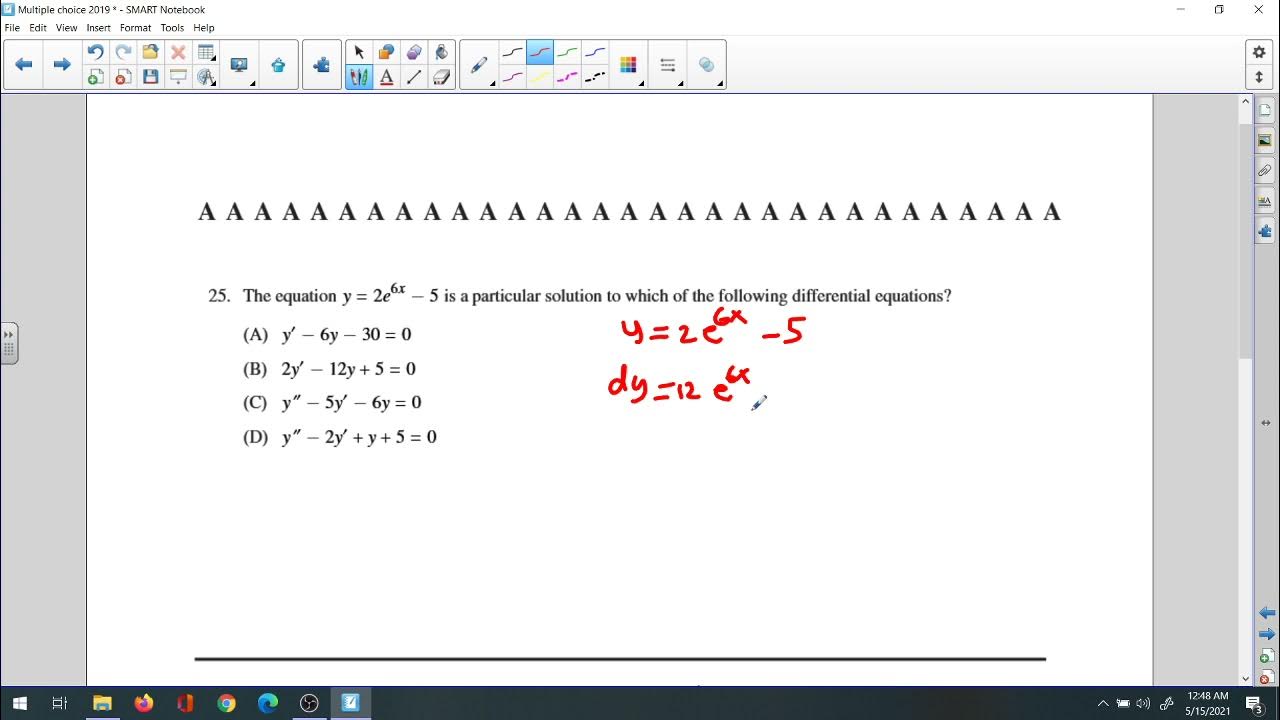
The exam required students to demonstrate proficiency in solving differential equations, both analytically and graphically.
Advanced topics such as Taylor and Maclaurin series were tested, assessing students' ability to approximate functions.
Real-world data interpretation using calculus principles was emphasized, bridging theoretical knowledge with practical application.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: