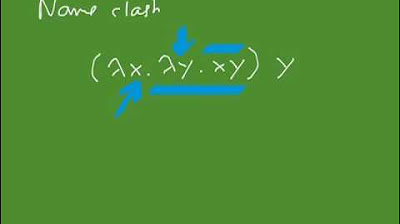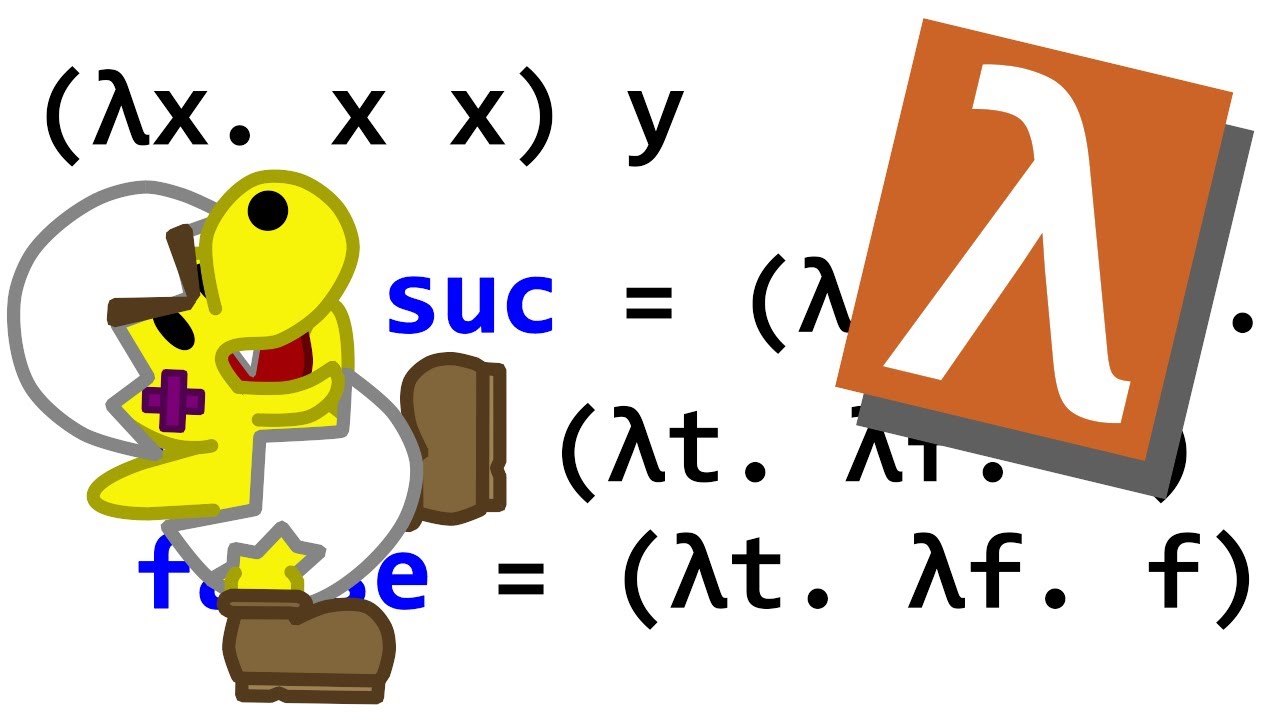Lambda Calculus Then and Now
TLDRThis script delivers a historical overview of the development of lambda calculus and its profound impact on computer science. It highlights the pioneering work of Alonzo Church and Alan Turing, who independently addressed the undecidability of first-order logic. The talk also touches on the significance of lambda calculus in defining functions and data structures, its connection to computation, and its influence on type theory, programming languages, and category theory. The speaker invites feedback on the timeline and bibliography provided, emphasizing the continuous evolution and 'recycling' of lambda calculus throughout the decades.
Takeaways
- 😀 The speaker expresses regret for not having more opportunities to collaborate with Michael Rabin, a Turing Award recipient, and sends warm greetings to him for an upcoming Turing conference.
- 📚 The speaker has prepared a timeline and a bibliography on the development of computer science and seeks feedback to ensure a fair representation of historical developments.
- 🔄 The lambda calculus is described as a method for explicit definitions of functions, emphasizing its foundational role in computer science and its ability to be 'recycled' effectively across decades.
- 🤖 The speaker discusses the historical context of the lambda calculus, including its development by Alonzo Church and its connection to the work of Alan Turing, highlighting the importance of logic and computability in their work.
- 🧩 The lambda calculus is shown to have a model in terms of sets of integers, with a focus on enumeration operators and the representation of data structures through lambda expressions.
- 🔢 The speaker explains how lambda calculus can represent integers, successor functions, and operations like addition and multiplication, demonstrating its utility in computational theory.
- 🔗 The connection between lambda calculus and computability is discussed, with the speaker noting that the type-free lambda calculus has the potential for self-replication, a key insight recognized by Turing.
- 📈 The speaker mentions the influence of lambda calculus on the development of computer languages and the importance of recursive procedures, emphasizing the role of pioneers like Church, Curry, and Kleene.
- 🌐 The timeline provided by the speaker covers significant developments in computer science from the mid-20th century onwards, highlighting the evolution of computing languages, type theory, and the intersection of logic and category theory.
- 🔮 The speaker concludes by discussing future directions in computer science, including the potential integration of topology and homotopy theory with computational models, suggesting a continued evolution of the field.
Q & A
Why was the speaker sad at the beginning of the talk?
-The speaker was sad because Michael Rabin, a Turing Award recipient, was not present at the event. The speaker also mentioned that Rabin would be giving a talk at the next Turing conference in Manchester.
What did the speaker regret about their academic career?
-The speaker regretted not having more opportunities to collaborate with Michael Rabin, as they only had two short periods of collaboration.
What is the significance of the lambda calculus in the context of the talk?
-The lambda calculus is significant because it has been recycled effectively every decade due to its basic ingredients, making it a versatile tool in various fields.
What is the historical connection between Alonzo Church and Alan Turing?
-Both Church and Turing independently applied ideas about logic and computability to show that first-order logic had no algorithmic decision procedure. They later met at Princeton, where Turing was a visitor and then a graduate student.
Why did Alonzo Church choose the lambda symbol for his calculus?
-Church chose the lambda symbol for his calculus as a playful choice, as indicated by his annotation 'eeny meeny, miny moe' on a postcard, rather than for any specific logical reason.
What is the lambda calculus model and how was it discovered?
-The lambda calculus model is a way to represent data structures and functions using lambda expressions. It was discovered independently by Myhill and Shepherdson, and by Richard Freiburg and Hartley Rogers, but it took another 20 years for it to be recognized as a model for lambda calculus.
What is the connection between lambda calculus and computability?
-The connection between lambda calculus and computability lies in the ability of lambda calculus to represent data structures and operations on them, which can be used to model computation.
What was the significance of the Turing machine in the context of the decision problem?
-The Turing machine was significant in the decision problem because it provided a model of computation that showed that deduction from a finite number of axioms is equivalent to watching a Turing machine run, thus making deduction undecidable.
What is the Church-Turing thesis and why was it accepted?
-The Church-Turing thesis states that any effectively calculable function can be computed by a Turing machine. It was accepted when it was shown that all the different models of computation, including lambda calculus, could be made equivalent.
How has lambda calculus influenced the development of computer languages?
-Lambda calculus has had a profound influence on the development of computer languages, particularly in the areas of type theory and recursive function theory, and has been used in the design of many programming languages.
Outlines
😔 Regret Over Missed Collaborations and Introduction to Lambda Calculus
The speaker expresses sadness over not having the opportunity to collaborate more with Michael Rabin, a Turing Award recipient, who is not present at the event. They invite the audience to extend their warm greetings to Rabin at an upcoming Turing conference. The speaker also reflects on their academic career and their regret over not collaborating with Rabin for a longer period. The main topic of the talk is introduced: a historical overview of the development of the lambda calculus, which the speaker describes as having been effectively 'recycled' every decade due to its foundational nature. The speaker invites feedback on a timeline and bibliography they have prepared, which are available on the ACM site, to ensure a fair representation of the developments over a long period.
🤔 The Origins and Development of Lambda Calculus
The speaker delves into the history of lambda calculus, highlighting the contributions of Alonzo Church and Alan Turing. They discuss how Church and Turing independently applied ideas about logic and computability to demonstrate the undecidability of first-order logic. The speaker also mentions the influence of Kurt Gödel's work and the role of Max Newman in Turing's career. The lambda calculus is described as a method for explicit definitions of functions, initially developed by Church to avoid the Russell paradox. The speaker notes the simplicity of the lambda calculus and its ability to represent functions, arguments, and values in an untyped system. The talk also touches on the lambda calculus's connection to the Church-Turing thesis, which equates the lambda calculus with Turing machines in terms of their computational capabilities.
📚 The Lambda Calculus as a Model for Computability
The speaker continues to explore the lambda calculus, focusing on its role as a model for computability. They discuss the early work of Church and Turing, and how the lambda calculus was initially part of a larger logical system. The speaker explains how Church's students found inconsistencies in this system, leading to the lambda calculus being separated from the rest. The speaker then describes a model for the lambda calculus using sets of integers, explaining how this model can represent functions and data structures. They also touch on the lambda calculus's ability to simulate data structures and its connection to the Church-Turing thesis, emphasizing the importance of understanding the lambda calculus in the context of computability.
🔢 Lambda Calculus and Computability: Representing Data Structures
The speaker discusses the lambda calculus's ability to represent data structures and its implications for computability. They explain how lambda expressions can act as stored computer programs, capable of being both data structures and operators. The speaker highlights Church's approach to interpreting integers using iterators and how this can be represented in lambda calculus. They also mention Turing's realization of the lambda calculus's potential for self-replication through the fixed-point theorem. The speaker emphasizes the importance of understanding the lambda calculus in the context of data structures and its role in the Church-Turing thesis, which posits that the lambda calculus can simulate any form of computation.
🤓 The Church-Turing Thesis and the Decision Problem
The speaker addresses the Church-Turing thesis and the decision problem, focusing on the question of whether first-order logic is recursively enumerable or decidable. They discuss Church's approach, which was based on Gödel's work, and Turing's solution, which involved the universal Turing machine. The speaker explains how the Church-Turing thesis was ultimately accepted when it was shown that all these models could be made equivalent. They also touch on the work of Emily Post, who independently thought of the idea of a Turing machine but did not put it in the same context. The speaker concludes by highlighting the importance of the Church-Turing thesis in understanding the limits of computability and the role of the lambda calculus in this discussion.
💻 The Evolution of Lambda Calculus and Its Influence on Computing
The speaker provides a timeline of the evolution of lambda calculus and its influence on computing. They mention the introduction of simple type theory by Church and its impact on the work of Leon Henkin, who developed new completeness proofs. The speaker also discusses the development of recursive function theory by Kleene and the influence of category theory on the lambda calculus. They highlight the importance of the 1950s, when computers and computer languages began to emerge, and the 1960s, which saw significant developments in category theory. The speaker concludes by noting the ongoing influence of lambda calculus in the development of new computing languages and its potential future applications in areas such as automated theorem proving and proof assistance.
🌐 The Future of Lambda Calculus: Connections with Topology and Homotopy Theory
The speaker concludes the talk by discussing the future of lambda calculus, highlighting its potential connections with other models, particularly topology and homotopy theory. They mention the work of Auskey at the Institute for Advanced Study, who has explored the idea of connecting lambda calculus with these mathematical fields. The speaker explains how the rules for homotopy theory align with the concept of intentional identity, which is concerned with the way things are defined rather than their extensional properties. They conclude by emphasizing the ongoing development and potential future applications of lambda calculus, inviting the audience to consider its role in the broader context of mathematical and computational theory.
Mindmap
Keywords
💡Lambda Calculus
💡Turing Award
💡Computability
💡Church-Turing Thesis
💡Recursive Function Theory
💡Type Theory
💡Undecidability
💡Combinators
💡Denotational Semantics
💡Homotopy Theory
💡Programming Languages
Highlights
Speaker expresses sadness over Michael Rabin's absence and hopes to see him soon.
Speaker regrets not having more opportunities to collaborate with Michael Rabin.
Invitation to give feedback on the ACM site's timeline and bibliography.
Historical overview of lambda calculus and its influence, with a focus on Alonzo Church and Alan Turing.
Discussion on the undecidability of first-order logic by Church and Turing.
Max Newman's role in Turing's invitation to Princeton and Turing's disappointment with the reception of his paper.
Introduction to lambda calculus as a method for explicit definitions of functions.
Explanation of lambda abstraction and its role in defining functions.
Church's choice of the lambda symbol and its relation to other mathematical symbols.
The lambda calculus model using sets of integers and enumeration operators.
Connection between lambda calculus and computability, with Turing's realization of self-replication in lambda calculus.
Church's interpretation of integers using lambda calculus and the simplicity of representing arithmetic operations.
The Church-Turing thesis and the acceptance of lambda calculus as a model of computation.
Emil Post's independent idea of a computing machine and his work on the word problem for semigroups.
Curry's introduction of combinators and their impact on lambda calculus.
The influence of lambda calculus on type theory and the work of Leon Henkin.
The development of recursive function theory by Kleene and its connection to lambda calculus.
The role of category theory in connecting different mathematical structures and its relation to lambda calculus.
The emergence of computer languages in the 1950s and their connection to lambda calculus and combinatory logic.
The 1970s as a pivotal decade for the convergence of logic, category theory, and the development of programming languages.
The 1980s and the connection between automated theorem proving and computer languages.
The 1990s and the ongoing development of programming languages and category theory.
Future prospects of connecting lambda calculus with topology and homotopy theory.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: