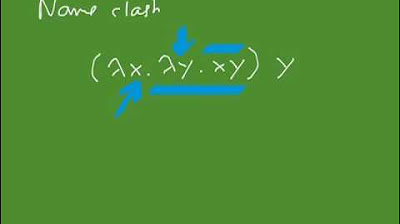L16: Lambda Calculus Introduction
TLDRThis lecture introduces the second half of a class focused on building programming languages, emphasizing the lambda calculus, a mathematical formalism for computation. It discusses the basics of lambda calculus, including variables, lambda abstractions, and applications, and introduces beta reduction as a key concept for computation. The Church-Turing thesis is also mentioned, highlighting the equivalence of lambda calculus and Turing machines in expressing computable functions.
Takeaways
- 🎓 The class is divided into two halves, with the first focusing on preparatory skills like programming, recursion, and interpreters, while the second half is dedicated to building programming languages with the concept of being Turing complete.
- 🤖 Lambda calculus was introduced by Alonzo Church in the 1930s as a mathematical foundation for computation, aiming to define what it means to compute something.
- 🔢 Lambda calculus syntax includes variables, lambdas for binding single named arguments, and applications for function application.
- 📝 The original lambda calculus is strict, allowing only single arguments for functions and applications, but techniques like currying can be used to handle multiple variables.
- 🤝 Church and Turing worked together to formalize the concept of computation, leading to the Church-Turing thesis, which posits that Turing machines and lambda calculus are equivalent in expressivity.
- 🔄 Beta reduction is a fundamental concept in lambda calculus, allowing the application of a lambda expression to an argument by substituting the formal parameter with the argument within the body of the lambda.
- 🔍 The lambda calculus does not specify how terms should be reduced; a reduction strategy is needed to turn it into a computational model.
- 🔁 The omega combinator is a non-terminating lambda term that loops infinitely and serves as the basis for implementing loops in lambda calculus.
- 🔑 The concept of 'beta reduction' is central to understanding computation within the lambda calculus, where a lambda expression can be reduced by substituting its parameter with the provided argument.
- 🛠 The script hints at further exploration of lambda calculus in upcoming lectures, including more examples, reduction strategies, and the implementation of the lambda calculus into a working language.
- 📚 The class also introduces the idea of translating higher-level programming languages into lambda calculus using Church or Comb encodings, which will be a project in the course.
Q & A
What is the main focus of the second half of the class as described in the transcript?
-The second half of the class focuses on applying the skills learned to build students' own programming languages that are Turing complete.
Who introduced the lambda calculus, and what was the purpose behind it?
-Alonzo Church introduced the lambda calculus in the 1930s to provide a mathematical underpinning for what it meant to be able to compute something.
What is the significance of the Church-Turing thesis in the context of the lambda calculus and Turing machines?
-The Church-Turing thesis states that both Turing machines and the lambda calculus are equivalent in terms of the expressivity to capture any computable function, making them a basis for computation.
What is the syntactical structure of the lambda calculus in its traditional form?
-In its traditional form, the lambda calculus consists of variables, lambdas that bind a single named argument, and applications where a function is applied to an argument.
How is the lambda calculus syntax represented in a more Scheme-inspired style?
-In a Scheme-inspired style, variables are represented as symbols, lambdas are represented with parentheses and the lambda keyword, followed by an argument and a body expression, and applications are represented with a function followed by an argument in parentheses.
What is the purpose of the 'experha' type predicate mentioned in the script?
-The 'experha' type predicate is used to determine whether a given expression is a valid lambda calculus expression, identifying symbols, lambda abstractions, and applications.
What is the concept of beta reduction in the lambda calculus?
-Beta reduction is the process of substituting the argument of a lambda expression for every occurrence of the formal parameter within the body of the lambda, resulting in a new term.
Why is the term 'omega' used in the context of the lambda calculus?
-The term 'omega' is used to denote a specific non-terminating lambda calculus expression that reduces to itself indefinitely, serving as the basis for implementing loops in lambda calculus.
What is the 'Y combinator' in the lambda calculus, and what does it enable?
-The Y combinator is a generalization of the omega combinator that allows for recursion of an arbitrary style using only lambda calculus terms, without the need for a built-in recursion operator.
What are reduction strategies in the context of the lambda calculus, and why are they important?
-Reduction strategies are methods for determining how to apply reduction rules to lambda calculus expressions to transform them into a computational system. They are important because the lambda calculus itself does not specify how terms should be reduced.
How does the concept of 'capture avoiding substitution' relate to the implementation of the lambda calculus?
-Capture avoiding substitution is a technique used to ensure that when substituting variables in the lambda calculus, the substitution does not inadvertently capture variables from the surrounding scope, which is crucial for correctly implementing the lambda calculus.
Outlines
📚 Introduction to Lambda Calculus
The video script begins with a recap of the first half of the class, which focused on foundational skills such as programming, Racket programming with structured data, recursion, and basic concepts of interpreters. The second half promises to be more engaging, as it delves into building programming languages that are Turing complete. The instructor introduces the concept of Turing completeness and the Lambda Calculus, originally formulated by Alonzo Church in the 1930s. Church aimed to provide a mathematical foundation for computation, leading to the definition of the Lambda Calculus through reduction sequences. The script also mentions Turing machines as an equivalent formulation in terms of expressivity and minimalism. The Lambda Calculus syntax is explained, including variables, lambdas, and applications, with a transition to a more Scheme-inspired style for easier interpretation in subsequent lectures.
🤖 Church-Turing Thesis and Lambda Calculus Forms
The script continues with a discussion on the Church-Turing thesis, which posits that Turing machines and the Lambda Calculus are both foundational for computation, capable of encoding and solving any computable function. Despite potential differences in complexity, both systems can theoretically handle any problem solvable by a computer. The instructor also touches on the concept of Church encoding, which allows translating Scheme or Racket programs into the Lambda Calculus. The lecture then explores Lambda Calculus forms in detail, such as lambda abstraction, application, and variables. Lambda abstraction is likened to a universal quantifier in higher-order logics, hinting at the Curry-Howard isomorphism. Applications involve functions and arguments, while variables are bound by lambdas during function application. The concept of computation in the Lambda Calculus is introduced through reductions, which define equivalences between terms, but the specifics of reduction strategies are left for future discussion.
🔍 Beta Reduction and Recursive Functions
This paragraph delves into the specifics of beta reduction, a fundamental concept in the Lambda Calculus. Beta reduction involves substituting the formal parameter within the body of a lambda expression with an actual argument, resulting in a new term. The instructor provides a formal definition of the beta rule and illustrates it with examples, showing how a lambda expression can be repeatedly reduced. The script introduces the omega combinator, a non-terminating program that serves as the basis for implementing loops in the Lambda Calculus. The instructor also hints at the y combinator, which will be discussed in future lectures and enables recursion using only Lambda Calculus terms. The lecture concludes with an invitation to explore more examples of the Lambda Calculus and its reductions in upcoming classes, emphasizing the importance of understanding beta reduction and the potential for turning the Lambda Calculus into a computational model.
🎬 Conclusion and Anticipation for Future Lectures
The script concludes with applause and music, signaling the end of the lecture. The instructor briefly acknowledges the audience and prepares for the next session. The focus is on ensuring that the audience has grasped the key concepts discussed, particularly the significance of beta reduction in the Lambda Calculus. The instructor also teases future lectures that will cover more examples of Lambda Calculus reductions and delve into reduction strategies, capture-avoiding substitution, and the implementation of the Lambda Calculus as a language. The anticipation is set for a deeper exploration of these topics, promising a comprehensive understanding of how the Lambda Calculus can be utilized in programming and computation.
Mindmap
Keywords
💡Lambda Calculus
💡Turing Complete
💡Alonzo Church
💡Reduction Sequence
💡Turing Machines
💡Beta Reduction
💡Church-Turing Thesis
💡Functional Programming
💡Currying
💡Omega Combinator
💡Y Combinator
Highlights
The second half of the class focuses on building programming languages that are Turing complete.
Lambda calculus was introduced by Alonzo Church in the 1930s as a mathematical underpinning for computation.
Lambda calculus involves variables, lambdas that bind single named arguments, and applications of functions.
The original lambda calculus syntax is shown, followed by a Scheme-inspired style.
Lambda calculus expressions can be easily represented in Racket using type predicates.
Church and Turing worked together to formalize computation, leading to the Church-Turing thesis.
The Church-Turing thesis states that Turing machines and lambda calculus are both bases of computation.
Lambda calculus forms the basis of functional programming languages like Lisp and Scheme.
Computation in lambda calculus is done via reductions, which define equivalent terms.
Beta reduction is a fundamental reduction in lambda calculus, applying a lambda to an argument.
Beta reduction can be performed repeatedly, as shown with the omega combinator.
The omega combinator is a non-terminating program and the basis for implementing loops in lambda calculus.
The y combinator will be introduced to enable recursion using only lambda calculus terms.
Lambda abstraction is a key form in lambda calculus, binding a formal parameter within a function body.
Applications in lambda calculus require a function in the function position and an argument in the argument position.
Variables in lambda calculus are only defined or assigned when function application occurs.
Reduction strategies are necessary to turn lambda calculus into a computational model.
Capture avoiding substitution is a method for implementing lambda calculus, to be discussed in future lectures.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: