Math Antics - Long Division with 2-Digit Divisors
TLDRThis Math Antics video teaches long division with multi-digit dividends and divisors. It demonstrates how to break down complex division into manageable steps, starting with smaller chunks of the dividend when the divisor is larger. The video emphasizes the importance of estimation and rounding for easier calculations, ultimately suggesting calculators for more complex problems.
Takeaways
- 📚 The video introduces a method for handling long division with multi-digit dividends, emphasizing breaking down the problem into smaller, more manageable steps.
- 🔢 The key to solving these problems is to divide the dividend digit-by-digit, starting with how many times the divisor fits into the first digit of the dividend.
- 🔄 When the divisor is a single-digit number, the process is straightforward, as demonstrated in the first example where dividing by 2 is shown.
- ❌ If the divisor is larger than the first digit of the dividend, you must group more digits together. This is illustrated when dividing by 8, where the first two digits of the dividend are considered together.
- 📈 The method can be adapted for divisors with more digits, such as two-digit numbers, but this requires estimating or guessing the multiples of the divisor, which can be more challenging.
- 📉 The video illustrates that taking larger chunks of the dividend for division can reduce the number of steps but increases the difficulty of each step, similar to climbing stairs with fewer, larger steps.
- 🤔 Estimation plays a crucial role in handling division with two-digit divisors, as it helps in making educated guesses about how many times the divisor fits into the dividend.
- 🔄 When the divisor is larger than the part of the dividend being considered, it necessitates grouping more digits together, which can make the problem more complex.
- 🧮 The video suggests that for very complex division problems, especially with large divisors, using a calculator is a practical solution.
- 💡 The script highlights the importance of practicing and understanding the division process, but also acknowledges that calculators can be a helpful tool for solving complex problems.
Q & A
What is the main focus of the 'Long Division' video?
-The video focuses on how to handle long division problems with multi-digit dividends and divisors, explaining the process of breaking down big division problems into smaller, more manageable steps.
What is the key strategy in solving long division problems as described in the video?
-The key strategy is to break up a big division problem into a series of smaller and easier division steps, often by dividing the dividend one digit at a time or in larger chunks if necessary.
How does the video illustrate the process of dividing by a one-digit divisor?
-The video uses an example where the dividend is divided digit-by-digit, starting with how many times the divisor fits into the first digit, then bringing down the next digit and repeating the process until the entire dividend is divided.
What happens when the first digit of the dividend is less than the divisor?
-If the first digit of the dividend is less than the divisor, you group the first two digits together and start the division process from there, as shown in the example where '8' is the divisor and '52' is the first two digits of the dividend.
Why is it beneficial to take bigger chunks of the dividend during division?
-Taking bigger chunks of the dividend can result in fewer division steps, making the process seem less cumbersome. However, it also makes each division step more challenging as the numbers involved are larger.
How does the video handle division problems with two-digit divisors?
-The video demonstrates that with two-digit divisors, you often need to group the first two digits of the dividend and estimate the quotient, as multiples of two-digit numbers are not typically memorized.
What is the role of estimation in solving division problems with two-digit divisors?
-Estimation is crucial in solving division problems with two-digit divisors as it helps in making educated guesses about the quotient, especially when the exact multiples are not easily recalled from the multiplication table.
Why might complex division problems be better solved using a calculator according to the video?
-The video suggests that complex division problems, especially those with two or more digit divisors, can be time-consuming and prone to errors when done manually. Calculators can provide quick and accurate results, making them a more efficient tool for such problems.
What is the significance of rounding numbers in the context of the video?
-Rounding numbers helps in making better estimates during division, especially when dealing with two-digit divisors. It simplifies the process by allowing you to work with numbers that are easier to handle mentally or through basic multiplication.
How does the video conclude about the approach to long division problems?
-The video concludes that while it's important to understand the long division procedure, especially for two-digit divisors, using a calculator for complex division problems is more practical and efficient.
Outlines
📚 Introduction to Long Division with Multi-Digit Divisors
This paragraph introduces the concept of long division with multi-digit dividends and divisors. The speaker explains how to break down a complex division problem into simpler steps by dividing the dividend digit-by-digit. Two examples are given, one with a divisor of 2 and another with a divisor of 8. The process involves determining how many times the divisor fits into the dividend's digits and then subtracting the product from the dividend. The speaker emphasizes that while it's possible to take larger chunks of the dividend, it's generally easier to work with one or two digits at a time due to the simplicity of the calculations.
🔍 Exploring Two-Digit Divisors in Long Division
The speaker delves into the challenges of long division with two-digit divisors. They illustrate how the process differs from single-digit divisors by showing two new problems with the same dividend but different divisors. The first example uses a divisor of 24, and the speaker estimates the first digit of the quotient by comparing multiples of 24 to the dividend's first two digits. The second example uses a divisor of 88 and demonstrates the need to group more digits from the dividend to find the quotient. The speaker also discusses the importance of estimation in handling larger divisors and suggests using calculators for complex problems.
🧮 Mastering Long Division with Two-Digit Divisors
In this paragraph, the speaker continues to explore long division with two-digit divisors, emphasizing the importance of estimation and rounding to simplify the process. They work through a problem dividing 817,152 by 38, demonstrating how to estimate each digit of the quotient by rounding the dividend and divisor to more manageable numbers. The speaker shows that each division step involves two or three digits of the dividend and explains the need to adjust estimates based on the remainder. The paragraph concludes with a reminder that while it's important to understand the process, using a calculator for complex division is often more practical.
Mindmap
Keywords
💡Long Division
💡Dividend
💡Divisor
💡Digit-by-Digit
💡Remainder
💡Estimation
💡Multiplication Table
💡Chunking
💡Rounding
💡Calculator
💡Problem Solving
Highlights
Introduction to the concept of breaking down long division problems into smaller, manageable steps.
Explanation of how to handle division problems with larger divisors, such as two or three-digit numbers.
Demonstration of how the divisor's size affects the digit-by-digit division process.
Illustration of solving a division problem with a one-digit divisor, showing the step-by-step process.
Highlighting the importance of multiplying the divisor by the quotient to find the remainder.
Discussion on the challenges faced when the divisor is larger than the first digit of the dividend.
Strategy of grouping digits together when the divisor is too large to divide into the first digit alone.
Example of solving a division problem with a two-digit divisor, emphasizing the need for estimation.
Explanation of how to handle situations where the divisor is greater than the initial chunk of the dividend.
Demonstration of solving a division problem with a two-digit divisor, showing the process of estimation and adjustment.
Discussion on the trade-off between fewer division steps and the complexity of each step.
Introduction of the idea of using calculators for complex division problems with two or more digit divisors.
Advice on using estimation to simplify the division process and make better guesses.
Example of solving a complex division problem with a two-digit divisor, emphasizing the use of rounding for estimation.
Explanation of the importance of adjusting the estimate when the remainder is greater than or equal to the divisor.
Final demonstration of a long division problem with a two-digit divisor, showcasing the entire process.
Encouragement to practice division problems but also to recognize the utility of calculators in complex situations.
Transcripts
Browse More Related Video

Math Antics - Long Division

Mental Math Tricks - Addition, Subtraction, Multiplication & Division!

Polynomials - Long Division

Math Antics - Division With Partial Quotients

Introduction to long division | Multiplication and division | Arithmetic | Khan Academy
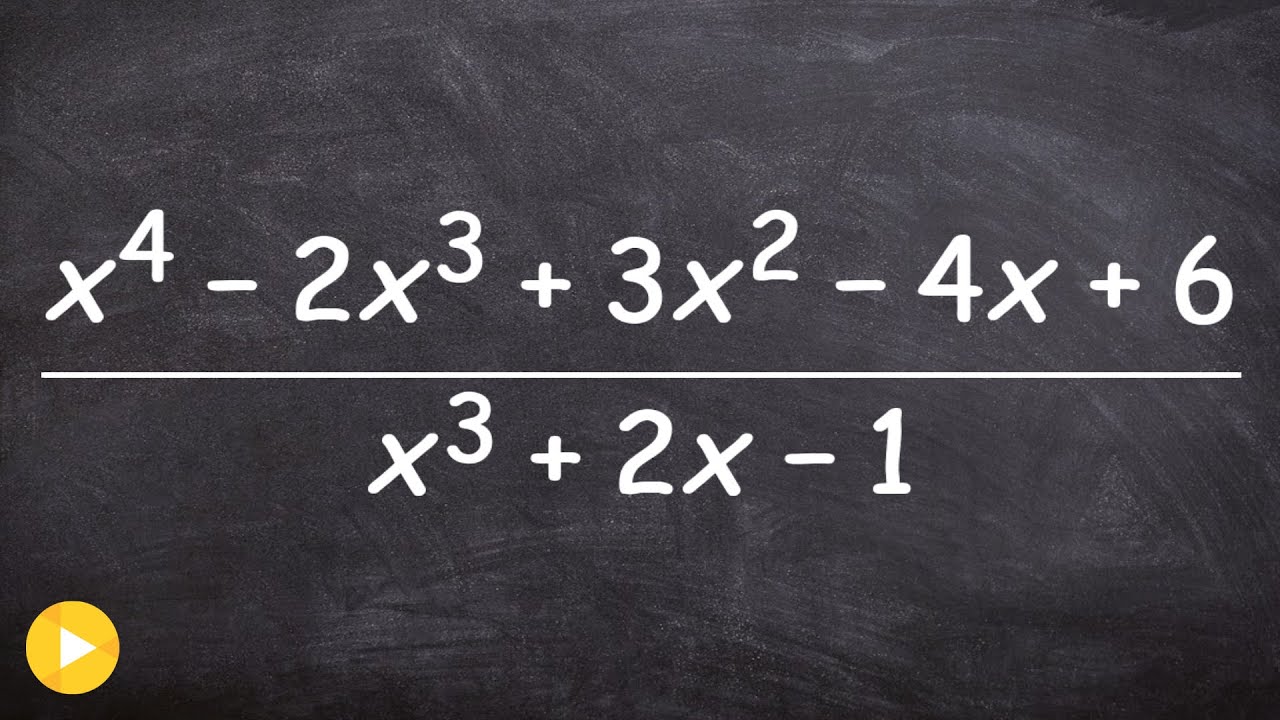
How to divide a trinomial into a polynomial using long division
5.0 / 5 (0 votes)
Thanks for rating: