Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration

blackpenredpen
25 Apr 201509:04
EducationalLearning
32 Likes 10 Comments

TLDRThis script outlines a method to calculate the work required to pump water out of a tank by considering it as horizontal rectangular slices. The process involves determining the volume of each slice using the dimensions and the equation of a line derived from the tank's triangular shape. The weight of water is calculated by multiplying the volume by the density and gravity. The work is then found by integrating the product of force and the distance each slice needs to be moved, resulting in a final answer in joules.

Takeaways
  • 📚 The concept of calculating work in physics is essentially force times distance.
  • 🔍 To find the force, one must determine the weight, which is calculated by volume times density.
  • 📏 The problem involves considering the tank as a series of horizontal slices, each with a different volume.
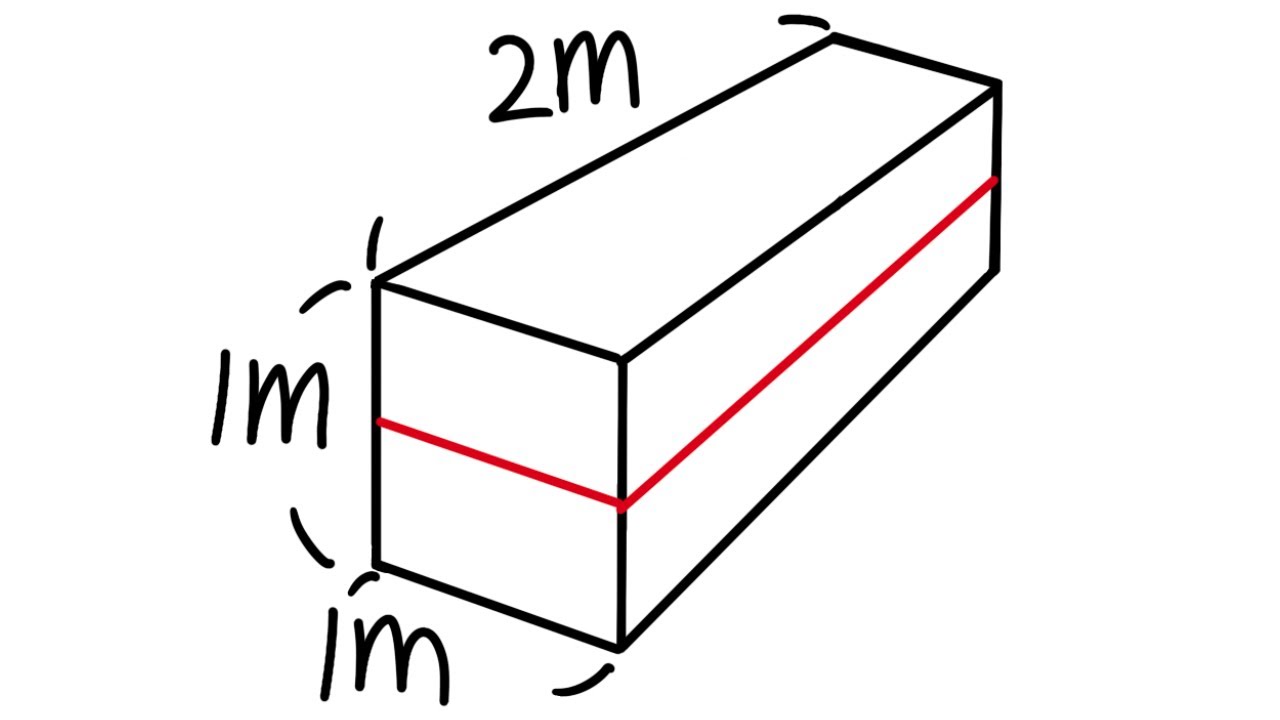
  • 📐 The shape of each slice is a horizontal rectangular box, with one side always being 8 meters long.
  • 📉 The length of the rectangle (front part) changes with the position of the slice, requiring an expression for its length.
  • 📊 The volume of each slice is expressed as 2x * 8 * Dy, where x is the horizontal distance and Dy is the thickness.
  • 📈 The relationship between x and y (the vertical position) is found by the slope of the triangle's side, resulting in x = 12y.
  • 💧 The volume formula for each slice is then 2 * 12y * 8 * Dy, incorporating the density of water and gravitational force.
  • 🚰 The work required to pump out each slice of water is the product of the volume, density, gravitational force, and the distance the water must travel.
  • 📏 The distance a slice of water must travel is calculated as 5 - y, considering the height of the tank and the position of the slice.
  • 📝 The final work to pump out all the water is found by integrating the work formula over the range of y from 0 to 3 meters, yielding a result in joules.
Q & A

  • What is the fundamental concept of calculating work in the context of pumping water out of a tank?

    -The fundamental concept of calculating work in this context is force times distance. Work is the product of the force required to move an object and the distance over which the force is applied.

  • How is force determined in the script?

    -In the script, force is determined by calculating the weight of the water, which is found by multiplying the volume of the water by its density.

  • What shape are the slices considered in the script when calculating the volume of water?

    -The slices considered in the script are horizontal rectangular boxes, which resemble the shape of a cell phone.

  • Why is the volume formula for the horizontal slices important?

    -The volume formula for the horizontal slices is important because it allows us to calculate the volume of each slice, which is necessary to determine the force and ultimately the work required to pump the water.

  • What is the significance of the triangle in the script?

    -The triangle is significant because it represents the front part of the horizontal slices, which changes in size as you move up the tank. The area of this triangle is used to determine the length of the rectangle in each slice.

  • How is the thickness of the slices represented in the script?

    -The thickness of the slices is represented by 'Dy', which signifies a small change in the y-axis, corresponding to the height of each horizontal slice.

  • What is the role of the X and Y coordinate system in the script?

    -The X and Y coordinate system is used to establish a reference for calculating the volume of the slices and to relate the changes in the x-direction (horizontal distance) to the y-direction (height or thickness of the slice).

  • How is the equation of the line representing the front part of the slices determined?

    -The equation of the line is determined by using the slope-intercept form (y = mx + b), where the slope (m) is the change in y over the change in x, and the y-intercept (b) is zero since it starts from the origin.

  • What is the significance of integrating the work formula in the script?

    -Integrating the work formula is significant because it allows us to calculate the total work required to pump all the water out of the tank by summing up the work for each individual slice from the bottom to the top of the tank.

  • What is the final result of the integral and what does it represent?

    -The final result of the integral is 10,584,000 Joules, which represents the total work needed to pump all the water out of the tank.

  • What is the unit for work in the SI unit system as mentioned in the script?

    -The unit for work in the SI unit system, as mentioned in the script, is the Joule (J).

Outlines
00:00
🔍 Calculating Work to Pump Water Using Horizontal Slices

This paragraph introduces the concept of calculating the work required to pump all the water out of a tank by considering horizontal slices. The speaker explains the basic principle of work as force times distance, where force is determined by the weight of the water, which in turn is calculated by volume times density. The method involves analyzing the shape of the slices, which are rectangular in this case, and determining the volume formula for these slices. The speaker also discusses the need to find an expression for the variable front part of the slices, which changes with the position in the tank, and introduces the use of a coordinate system to relate the dimensions of the slices to the position within the tank.

05:03
📚 Deriving the Volume Formula and Calculating Work

The speaker continues by deriving the volume formula for the rectangular slices of the tank. They establish a relationship between the dimensions of the slices and the position within the tank, using the equation of a line to connect the x and y coordinates. The volume of each slice is expressed as a function of y (the vertical position), and the speaker then integrates this formula to account for all the slices from the bottom to the top of the tank. The density of water and the gravitational constant are factored in to find the weight of each slice, which is then used to calculate the work needed to pump the water out. The final step involves integrating the work formula over the range of y values from 0 to 3 meters to find the total work required, which is given as 1058400 Joules.

Mindmap
Keywords
💡Work
In physics, 'work' is defined as the product of the force applied to an object and the distance over which it is applied. In the video, the concept of work is central to calculating the effort required to pump water out of a tank, where the work is essentially the force exerted by the water's weight times the distance it must be moved.
💡Force
'Force' is the push or pull upon an object resulting from its interactions. In the context of the video, force is crucial in determining the amount of work needed to move the water. The force here is equivalent to the weight of the water, which is calculated by volume times density.
💡Volume
The 'volume' of an object or substance is the quantity of three-dimensional space it occupies. In the script, the volume of water in the tank is considered by slicing the tank into horizontal sections, with each slice's volume being calculated to determine the total volume of water.
💡Density
'Density' is the mass per unit volume of a substance. For the water in the tank, its density is a key factor in calculating the weight of the water and, subsequently, the force and work required to pump it out.
💡Weight
'Weight' is the force exerted on a body due to gravity. In the video, the weight of the water is found by multiplying its volume by its density, which is then used to calculate the force needed to pump the water out of the tank.
💡Horizontal Slices
The term 'horizontal slices' refers to the method of dividing the water in the tank into thin, horizontal layers to simplify the calculation of volume and work. The script describes this process to break down the complex shape of the water in the tank into manageable rectangular prisms.
💡Rectangular Box
A 'rectangular box' is a three-dimensional shape with six faces, all of which are rectangles. In the video, the slices of water are likened to rectangular boxes to make it easier to calculate the volume of each slice and, by extension, the total volume of water in the tank.
💡Differential Element
A 'differential element' is a small part of a larger system used in calculus to analyze the system as a whole. In the script, 'Dy' represents a small change in the y-axis, used to describe the thickness of each horizontal slice of water.
💡Integration
'Integration' in calculus is the process of summing up all the differential elements to find a total quantity. In the context of the video, integration is used to calculate the total work required to pump all the water out of the tank by summing the work for each horizontal slice.
💡Joule
The 'Joule' is the SI unit of work or energy. In the video, the final answer for the work required to pump the water is given in Joules, indicating the total energy that would need to be expended.
Highlights

Calculating work needed to pump water out of a tank using the concept of force times distance.

Determining force by finding the weight, which is volume times density.

Using horizontal slices to analyze the tank's contents and calculate work.

Identifying the shape of slices as horizontal rectangular boxes.

Finding the volume formula for the rectangular box slices.

Recognizing that the front part of the box changes and requires an expression.

Using a triangle to represent the changing front part of the box.

Labeling the thickness of the slice as Dy in the y-axis direction.

Establishing an X and Y coordinate system with the origin at the top of the triangle.

Expressing the volume of the box slice in terms of 2x, 8, and Dy.

Connecting the X and Y values to relate the changing front part of the box.

Deriving the equation of the line representing the triangle's slope as y = (3/1.5)x.

Isolating X in terms of Y to substitute into the volume formula.

Writing the final volume expression as 2 * 12y * 8 * Dy.

Multiplying by water density and gravity to find the force on each slice.

Calculating the distance each water slice needs to travel to be pumped out.

Determining the work required to pump out each slice by multiplying force, volume, and distance.

Integrating the work expression over the range of y values from 0 to 3 meters.

Final answer for the total work needed to pump all water is 105,840 Joules.

Transcripts

Browse More Related Video

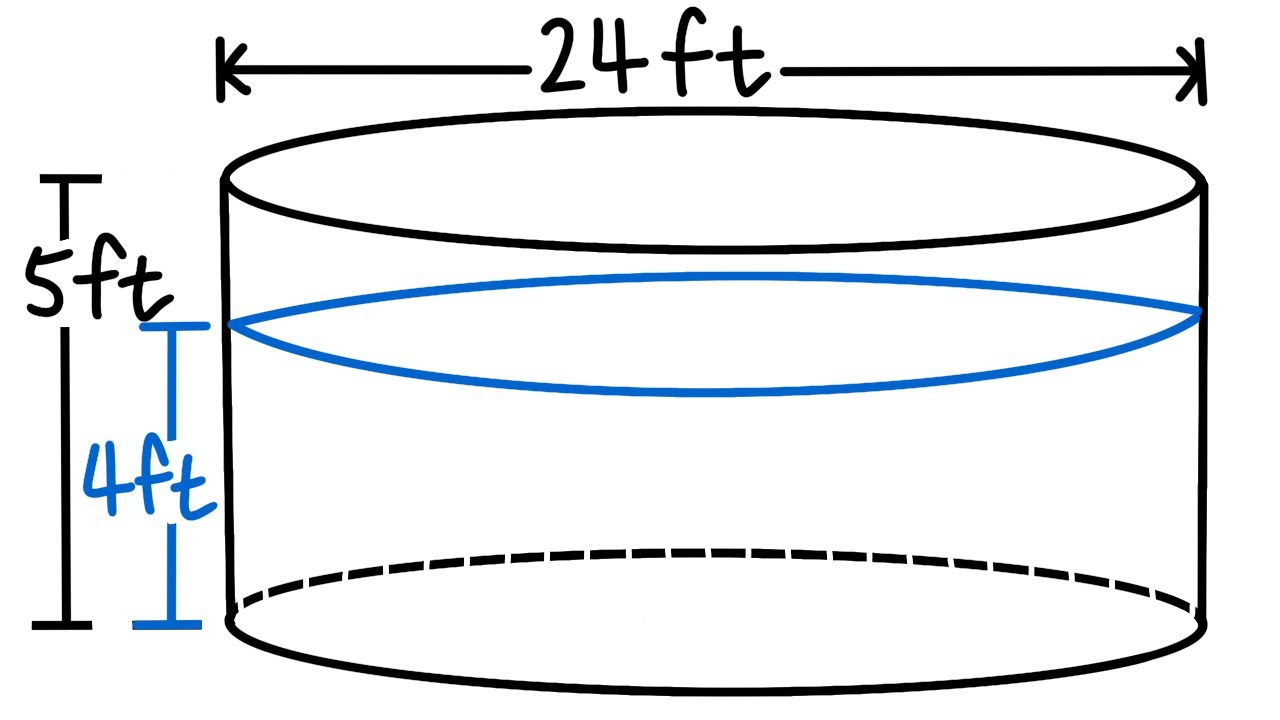
Calculating Work, pumping water out of a circular swimming pool

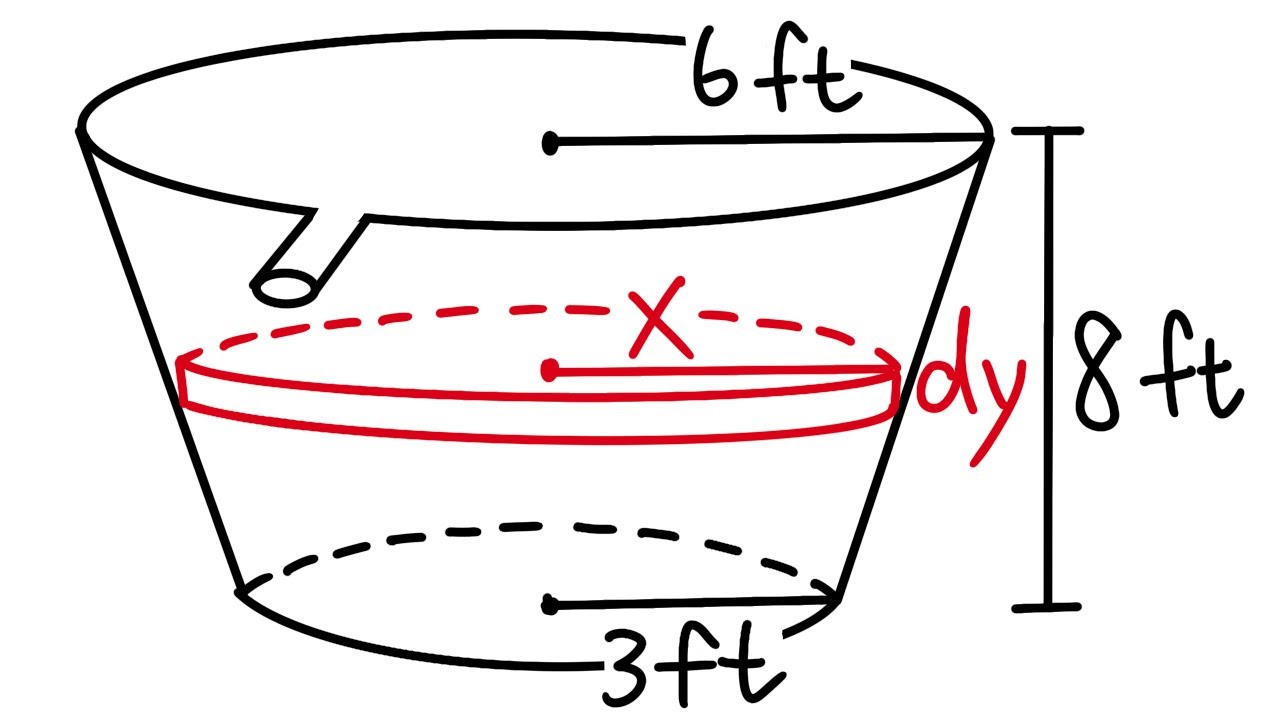
Pumping water out of a bucket, calculating work, calculus 2 tutorial

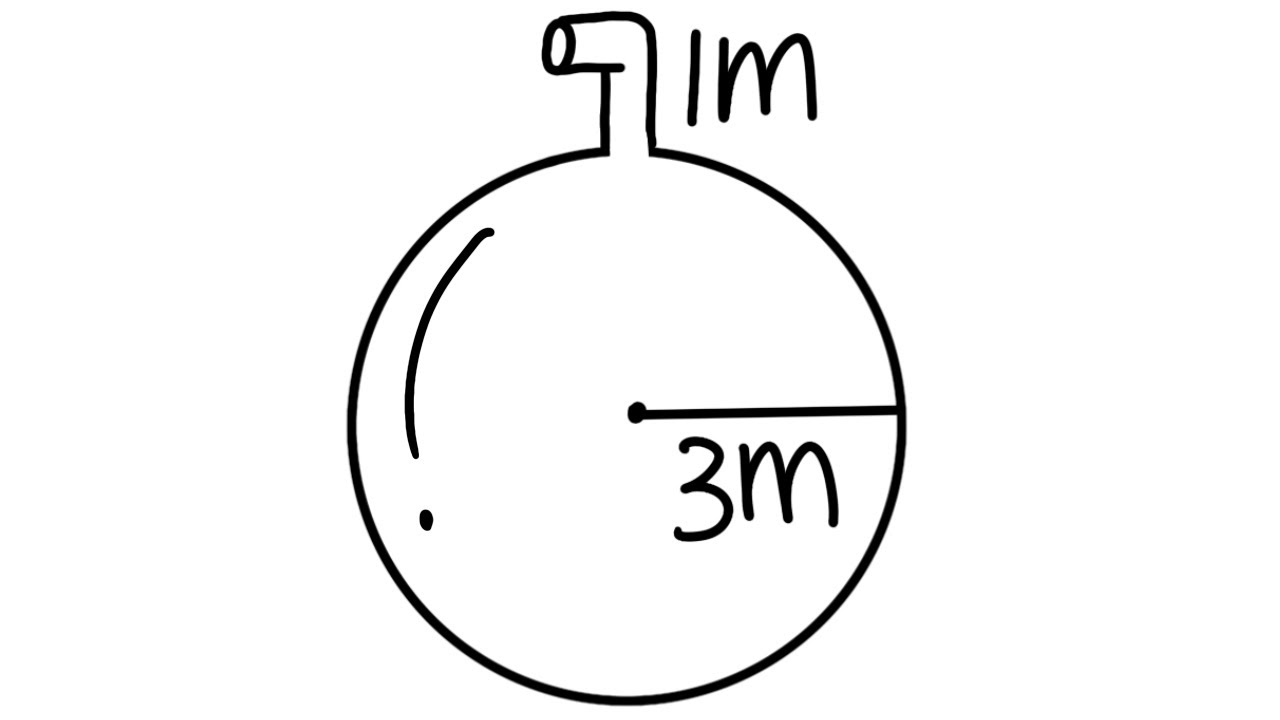
Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

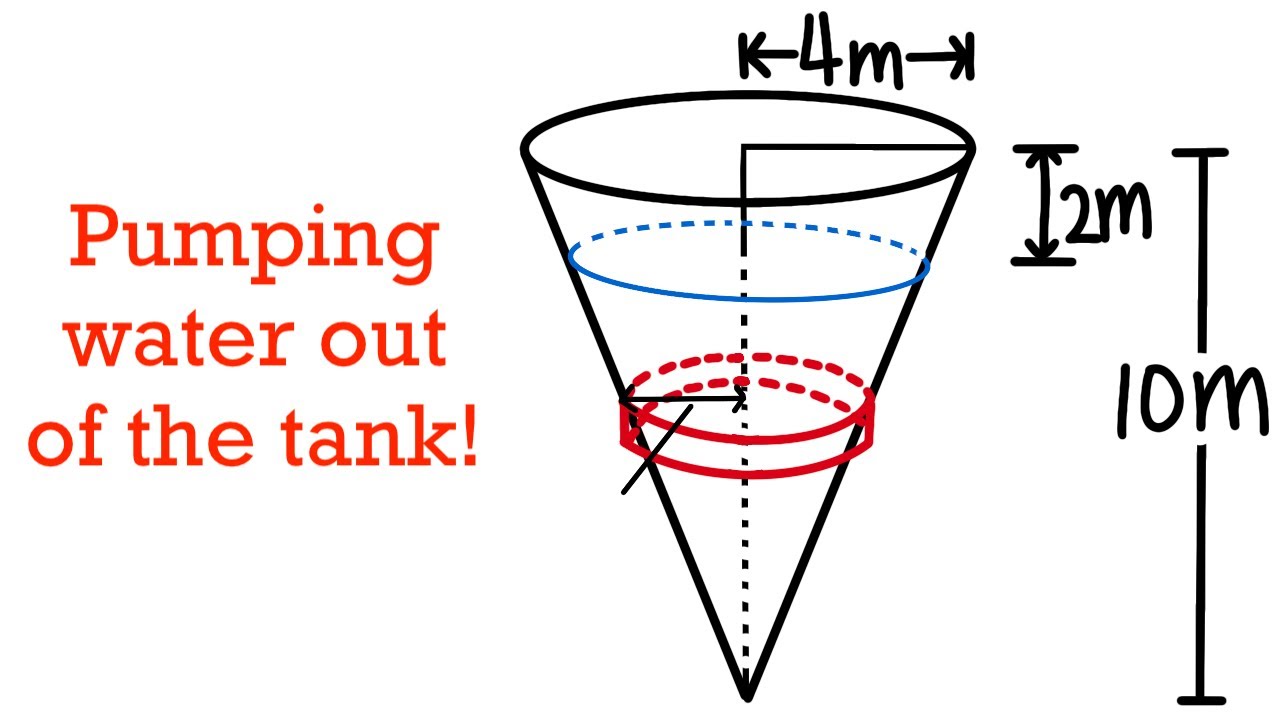
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

calculating work, pumping water out of a rectangular tank, calculus 2 tutorial

Calculus Work Pump Water From a Circular Swimming Pool

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics CalculationFluid MechanicsWork CalculationForce AnalysisVolume IntegrationDensity ApplicationPressure CalculationHydraulic EngineeringEducational ContentMathematical IntegrationEngineering Tutorial