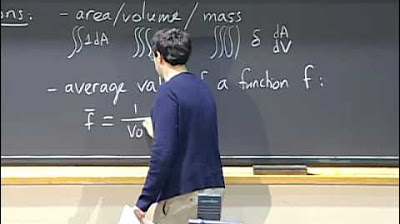ALL of calculus 3 in 8 minutes.
TLDRThis video script offers a concise overview of key concepts in calculus 3, including 3D vectors and surfaces, vector multiplication (dot product and cross product), limits and derivatives in multivariable functions, directional derivatives, double and triple integrals, and the use of polar, cylindrical, and spherical coordinates. It also touches on coordinate transformations and the Jacobian, as well as vector fields, scalar fields, and line integrals, highlighting the properties of divergence and curl. The script is designed to spark interest in the complex world of 3D calculus, with the promise of future videos for deeper exploration.
Takeaways
- 📈 Introduction to 3D space vectors and surfaces, emphasizing functions with two inputs (X, Y) and one output (Z).
- 🔢 Explanation of vector multiplication in 3D, including addition, subtraction, dot product, and cross product, with a focus on their spatial relationships and properties.
- 📊 Discussion on limits and derivatives of multivariable functions, highlighting directional derivatives and the concept of gradients.
- 🔍 Exploration of double integrals, including the process of calculating volumes under functions and the use of polar coordinates for non-rectangular regions.
- 🌐 Introduction to triple integrals and their application in calculating volumes and averages over 3D regions, using different coordinate systems.
- 🌀 Understanding of vector fields and scalar fields, their assignments to points in space, and the concept of line integrals.
- 🔄 Explanation of conservative vector fields, path independence, and the analogy to conservative forces like gravity.
- 📐 Conversion of integrals between different coordinate systems using Jacobians to account for coordinate system transformations.
- 🤓 Mention of the complexity and depth of the topics, suggesting further study and resources for deeper understanding.
- 🎓 Acknowledgment of the video's condensed format, with the intent to cover more in-depth content in future videos.
- 🔗 Promise of additional resources and links in the video description for those interested in further exploration.
Q & A
What is the main topic of the video?
-The main topic of the video is an overview of Calculus 3, covering various concepts such as 3D space vectors and surfaces, vector multiplication, limits and derivatives of multivariable functions, double and triple integrals, coordinate transformations with Jacobian, and vector fields, scalar fields, and line integrals.
What are 3D functions and how do they relate to 2D functions?
-3D functions are similar to 2D functions but they operate in three-dimensional space. They take two inputs on the X and Y axes and produce an output on the Z-axis. This is analogous to 2D functions, but extended into the third dimension.
What is the dot product and how is it related to the spatial relationship between two vectors?
-The dot product is a type of multiplication between two vectors where you multiply corresponding components and add the results. It has a spatial significance as the dot product of two perpendicular (orthogonal) vectors is zero, and for parallel vectors, it equals the product of their magnitudes.
How is the cross product of two vectors defined and what is its property?
-The cross product of two vectors can be expressed as the determinant of a matrix with unit vectors I, J, and K for X, Y, and Z directions, and the vectors V and U being multiplied. Its property is that it generates a vector that is orthogonal (perpendicular) to the two vectors being multiplied.
What are directional derivatives and how do they relate to the derivatives of 3D functions?
-Directional derivatives are the derivatives of a 3D function in a specific direction at a point. Unlike 2D functions, there are infinitely many derivatives for a 3D function at a point since there are infinitely many directions one can take.
How do double integrals work with multivariable functions and what is the concept of integrating over non-rectangular regions?
-Double integrals find the volume under a multivariable function. Instead of finding the area under a function as in single-variable calculus, you first integrate with respect to X, then integrate the resulting area with respect to Y. Integrating over non-rectangular regions involves using functions as bounds and polar coordinates, where the integral is in terms of r (radial distance) and θ (angular coordinate).
What are triple integrals and how are they used in calculating volumes?
-Triple integrals are used to calculate the volume of any 3D region that can be defined with three different boundaries. They involve integrating a function over a 3D region by setting up the boundaries for X, Y, and Z axes and integrating successively in each direction.
What are cylindrical and spherical coordinates, and how do they differ from Cartesian coordinates?
-Cylindrical coordinates consist of a radius r, a z-coordinate, and an angle θ, while spherical coordinates have a radius (rho), an angle Φ from the vertical line passing through the origin, and an angle θ similar to polar coordinates but in 3D space. These coordinate systems differ from Cartesian coordinates as they provide different ways to specify the position of a point in space.
What is the Jacobian and why is it used in coordinate transformations?
-The Jacobian is a function added to the integral when changing from one coordinate system to another. It accounts for the distortion or change in volume that occurs due to the transformation of coordinates, ensuring the integral is computed correctly in the new coordinate system.
What are vector fields and how do they relate to scalar fields?
-Vector fields assign a vector to each point in space, while scalar fields assign a scalar (regular number) to each point. Both can be thought of as 3D surfaces, with vector fields representing the direction and magnitude of quantities at each point in space.
What are the main properties of vector fields, Divergence and Curl, and what do they represent?
-Divergence represents the amount of outflow from a certain part of a vector field, with high divergence at the center and lower at points further away. Curl represents the amount of rotation around a certain point in a vector field, with low curl on the outside and high at the center where everything spins around it.
Outlines
📐 Introduction to 3D Calculus: Vectors and Surfaces
This paragraph introduces the viewer to the fundamental concepts of 3D calculus, highlighting the existence of functions in 3D space that take inputs on the X and Y axes and produce an output on the Z-axis. It explains the concept of vectors with direction and magnitude in three dimensions. The paragraph also touches on the idea of vector multiplication, including addition, subtraction, and the dot product, emphasizing the spatial relationship between vectors and how the dot product can reveal properties such as orthogonality and parallelism. The cross product is introduced as another form of vector multiplication, with its unique property of generating an orthogonal vector to the original two. The explanation is clear and concise, setting the stage for a deeper understanding of 3D calculus.
🔢 Vector Multiplication and Multivariable Functions
This section delves deeper into vector multiplication, discussing the dot product and its geometric interpretation, including the formula relating it to the angle between two vectors. It explains how the dot product is zero for perpendicular vectors and equal to the product of magnitudes for parallel vectors. The cross product is further elaborated, with its determinant form and the property of generating an orthogonal vector. The paragraph then transitions into discussing limits and derivatives in multivariable functions, including directional derivatives and the gradient vector. The concept of double integrals is introduced, explaining how they are used to calculate volumes under surfaces and how they can be applied to non-rectangular regions using functions and polar coordinates.
Mindmap
Keywords
💡3D space vectors
💡Vector multiplication
💡Dot product
💡Cross product
💡Limits and derivatives
💡Gradient
💡Double integrals
💡Triple integrals
💡3D coordinate systems
💡Coordinate transformations
💡Vector Fields
💡Divergence and curl
Highlights
Introduction to 3D space vectors and surfaces, emphasizing the existence of functions in 3D that take two inputs on the X and Y axes and produce an output on the Z-axis.
Explanation of vectors in 3D, highlighting that they have direction and magnitude, and their direction is three-dimensional.
Discussion on vector multiplication, including addition, subtraction, and the introduction of the dot product as the first type of multiplication.
Revelation of the dot product's spatial relationship, where perpendicular vectors have a dot product of zero and parallel vectors have a dot product equal to the product of their magnitudes.
Description of the cross product, another main way of multiplying vectors, which generates a vector orthogonal to the two being multiplied.
Introduction to limits and derivatives of multivariable functions, noting the existence of infinitely many derivatives at a point due to the many directions one can take.
Explanation of directional derivatives and how they relate to the gradient, a vector with components being the derivative in the X and Y directions.
Overview of double integrals, contrasting them with single-variable integrals by highlighting their use in finding volumes under functions instead of areas.
Discussion on integrating over non-rectangular regions and the use of polar coordinates for double integrals, emphasizing the change in integral bounds from numbers to functions.
Introduction to triple integrals, their use in integrating any 3D region defined by three boundaries, and their application in finding average values like temperature.
Explanation of 3D coordinate systems, including cylindrical and spherical coordinates, and their roles in simplifying integrals.
Discussion on coordinate transformations and the Jacobian, a function added to the integral to account for the distortion caused by switching coordinate systems.
Overview of vector fields, scalar fields, and line integrals, differentiating between scalar line integrals done over scalar fields and vector line integrals done over vector fields.
Explanation of conservative vector fields, their path independence, and their analogy to conservative forces like gravity.
Description of the properties of vector fields, namely divergence and curl, and how they relate to the amount of outflow and rotation around a point.
Acknowledgment of the video's condensed nature and the promise of future videos for deeper exploration of the topics discussed.
Invitation to explore additional resources online for further understanding of the concepts introduced in the video.
Transcripts
Browse More Related Video
The ENTIRE Calculus 3!
Introduction to the surface integral | Multivariable Calculus | Khan Academy
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Curl 3 | Partial derivatives, gradient, divergence, curl | Multivariable Calculus | Khan Academy
The Vector Dot Product
Cross Product and Dot Product: Visual explanation
5.0 / 5 (0 votes)
Thanks for rating: