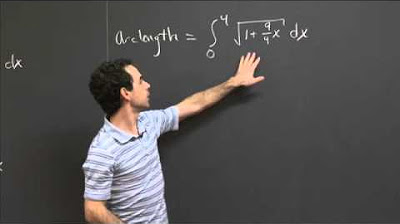Arc Length (Calculus 3)
TLDRThis Houston Mathprep video delves into calculating the arc length of a 3D curve defined by a vector-valued function. The instructor explains that while estimating this length can be challenging, integration simplifies the process. The video demonstrates two examples: one involving trigonometric functions and the other using logarithmic and polynomial functions. It shows how to find the derivative of the vector function, calculate the magnitude of this derivative, and then integrate it over the given interval to find the exact arc length. The examples illustrate the application of calculus concepts to solve real-world problems related to the geometry of curves.
Takeaways
- 📚 The video is an educational tutorial from Houston MathPrep, focusing on calculating the arc length of a 3D curve defined by a vector-valued function.
- 🔍 The concept of using integration to find the distance traveled along a curve in 3D space is introduced, as it's not easily estimated by visual inspection alone.
- 📏 An initial method of estimating the arc length involves breaking the curve into vectors and summing their lengths, but this is acknowledged as a rough approximation.
- 📈 The Mean Value Theorem and Fundamental Theorem of Calculus are mentioned as tools that allow for a more precise calculation of arc length as the number of vectors increases.
- 📘 The exact formula for arc length is presented as the definite integral from \( t = a \) to \( t = b \) of the magnitude of the derivative of the vector function, \( \|r'(t)\| \).
- 📝 The first example provided involves calculating the arc length of the function \( \vec{r}(t) = 3\cos(2t), 3\sin(2t), 2t \) over the interval from \( t = 0 \) to \( t = 2\pi \).
- 🧮 The calculation for the first example simplifies by recognizing a Pythagorean identity, leading to an integral of \( 2\sqrt{10} \) with respect to \( t \), resulting in \( 4\sqrt{10}\pi \).
- 📑 The second example involves the function \( \vec{r}(t) = \ln(t), 2t, t^2 \) over the interval from \( t = 1 \) to \( t = 4 \), with a focus on simplifying the integral before solving.
- 🔑 The second example's integral is simplified by recognizing a perfect square, leading to an integral of \( \frac{1}{t} + 2t \), which is then solved to find the arc length.
- 📊 The final result for the second example is the arc length from \( t = 1 \) to \( t = 4 \), calculated as \( \ln(4) + 16 - 1 \), simplifying to \( 15 + \ln(4) \).
- 👋 The video concludes with a sign-off, wishing viewers good luck with their arc length calculations and promising to see them in the next video.
Q & A
What is the main concept discussed in the video script?
-The main concept discussed in the video script is finding the arc length of a 3D curve defined by a vector-valued function using integration.
Why is it difficult to estimate the distance traveled on a 3D curve?
-It is difficult to estimate the distance traveled on a 3D curve because the curve can be twisting and turning through three dimensions, making it hard to eyeball the length without a systematic approach.
What is the initial method suggested in the script to approximate the total length along the curve?
-The initial method suggested is to approximate the total length by taking several vectors, placing them end to end, and then adding up the total length of these vectors.
How does the approximation method using vectors compare to the exact method?
-The approximation method using vectors is less accurate and more labor-intensive compared to the exact method, which uses integration to find the arc length.
What mathematical theorems are mentioned in the script that allow for a more precise calculation of arc length?
-The Mean Value Theorem and the Fundamental Theorem of Calculus are mentioned as allowing for a more precise calculation of arc length when the vector-valued function is differentiable on the interval from a to b.
What is the formula for the exact arc length from a to b on a curve?
-The exact formula for the arc length from a to b on a curve is the definite integral from t equals a to t equals b of the magnitude of the derivative of the vector-valued function with respect to t.
What is the first vector-valued function given as an example in the script?
-The first vector-valued function given as an example is 3 cosine of 2t, 3 sine of 2t, 2t, over the interval for t from 0 to 2 pi.
How is the derivative of the first vector-valued function calculated?
-The derivative of the first vector-valued function is calculated using the chain rule, resulting in -6 sine of 2t, 6 cosine of 2t, and 2 for the respective components.
What simplification is made when calculating the magnitude of the derivative of the first vector-valued function?
-The simplification made is recognizing that the sum of sine squared and cosine squared of 2t equals 1, which simplifies the magnitude calculation to the square root of 40, or 2 root 10.
What is the final result for the arc length of the first vector-valued function example?
-The final result for the arc length of the first vector-valued function example is 4 square root 10 times pi.
What is the second vector-valued function given as an example in the script?
-The second vector-valued function given as an example is ln of t, 2t, t squared, over the interval for t from 1 to 4.
How is the magnitude of the derivative of the second vector-valued function simplified?
-The magnitude of the derivative of the second vector-valued function is simplified by recognizing it as a perfect square, resulting in one over t plus 2t.
What is the final result for the arc length of the second vector-valued function example?
-The final result for the arc length of the second vector-valued function example is ln of 4 plus 16 minus 1, which simplifies to 15 plus ln of 4.
Outlines
📚 Introduction to Calculating Arc Length in 3D Space
The script begins with an introduction to the concept of finding the arc length of a curve in 3D space defined by a vector-valued function. The challenge of visualizing the distance traveled along such a curve is highlighted, and the use of integration is proposed as a method to tackle this problem. The script explains the process of approximating the total length by summing the lengths of vectors placed end to end along the curve. It also introduces the idea of improving the approximation by using more vectors, leading to the concept of definite integrals. The Mean Value Theorem and the Fundamental Theorem of Calculus are mentioned as the theoretical basis for this approach. The formula for the exact arc length is presented, involving the integral of the magnitude of the derivative of the vector function from 'a' to 'b'. The script then sets up two examples to illustrate the process: calculating the arc length of a function with a theme of '2t' over the interval from 0 to 2π.
📘 Detailed Calculation of Arc Length for Two Vector Functions
The second paragraph delves into the detailed process of calculating the arc length for two specific vector-valued functions. The first example involves the function 3cos(2t), 3sin(2t), 2t, and the script guides through the calculation of its derivative, the magnitude of the derivative, and the subsequent integration to find the arc length over the interval from 0 to 2π. A Pythagorean identity simplifies the integration process, leading to a final result of 4√10π. The second example features the function ln(t), 2t, t^2, where the script explains the derivation of the magnitude of its derivative, which factors into a perfect square, simplifying the integration. The anti-derivatives for the components of the magnitude are calculated, and the final arc length is found by evaluating the integral from 1 to 4, resulting in ln(4) + 16 - 1, which simplifies to ln(4) + 15. The script concludes by wishing the viewers success in their arc length calculations and anticipates the next video.
Mindmap
Keywords
💡3D Curve
💡Vector-Valued Function
💡Arc Length
💡Integration
💡Magnitude
💡Differentiable
💡Mean Value Theorem
💡Fundamental Theorem of Calculus
💡Chain Rule
💡Pythagorean Identity
💡Antiderivatives
Highlights
Introduction to calculating the distance traveled on a 3D curve using integration.
Explaining the difficulty of estimating the length of a curve that twists and turns in 3D space.
Using integration to find the exact formula for arc length on a curve.
Approximating total length by placing vectors end to end and adding their lengths.
Improving the approximation by using more vectors, but at the cost of more work.
The Mean Value Theorem and Fundamental Theorem of Calculus simplify the process of finding arc length.
The formula for arc length involves the magnitude of the derivative of a vector-valued function.
Example of calculating the arc length of a vector-valued function with components involving cosine and sine.
Deriving the formula for the magnitude of the derivative of a vector function.
Using the Pythagorean identity to simplify the integration process.
Calculating the integral to find the arc length of a curve from 0 to 2π.
Second example involving a vector-valued function with natural logarithm and quadratic terms.
Finding the derivative of the vector-valued function involving ln(t), 2t, and t squared.
Simplifying the integration process by recognizing a perfect square in the magnitude formula.
Calculating the integral to determine the arc length from t=1 to t=4.
Final solution for the arc length of the second example, involving natural logarithm and quadratic terms.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: