Equations of Planes: Vector & Component Forms | Multivariable Calculus
TLDRThis video script explores the concept of deriving equations for planes, building upon the foundation of line equations. It emphasizes the need for two key pieces of information: a specific point on the plane and a normal vector, which indicates the plane's orientation. The script illustrates the process of finding the equation of a plane by using the dot product between the normal vector and any vector lying on the plane, which must equal zero. An example is provided, demonstrating how to calculate the plane's equation using a given point and normal vector, ultimately simplifying the equation to a form that can be easily understood.
Takeaways
- 📚 The script discusses extending the concept of equations for lines to planes, requiring two key pieces of information: a point on the plane and a normal vector.
- 📍 A point on the plane is denoted as P_0(x_0, y_0, z_0), which is essential for defining the plane's position in three-dimensional space.
- 🧭 A normal vector is a vector that points directly away from the plane, indicating its orientation in space, and is crucial for the plane's equation.
- 📈 The normal vector is orthogonal to any vector lying in the plane, meaning the dot product of the normal vector and a vector on the plane is zero.
- 🔍 The script uses a low-tech analogy with a pen as the normal vector sticking out of a piece of paper, representing the plane.
- 🔢 The equation of the plane is derived from the dot product of the normal vector and the vector from a fixed point on the plane to any generic point on the plane, which equals zero.
- 📝 The specific example in the script uses a point P_0(1, 2, 3) and a normal vector (4, 5, 6) to illustrate the process of deriving the plane's equation.
- 🔄 The vector from P_0 to a generic point P(x, y, z) is calculated as (x - 1, y - 2, z - 3), which is then used in the dot product with the normal vector.
- 📉 The dot product results in an equation 4(x - 1) + 5(y - 2) + 6(z - 3) = 0, which simplifies to the plane's equation in component form.
- ✅ The simplified component form of the plane's equation from the example is 4x + 5y + 6z = 32, after moving constants to the other side of the equation.
- 📖 The script contrasts the component form of the plane's equation with the vector form, which has not been taught yet.
Q & A
What is the basic idea behind extending the equations for lines to planes?
-The basic idea is to provide two pieces of information to define a plane, similar to how a point and a direction vector define a line. For planes, one piece is a specific point on the plane and the other is a normal vector that indicates the plane's orientation.
What is a normal vector and why is it important in defining a plane?
-A normal vector is a vector that points directly away from the plane, indicating its orientation. It is important because it defines the tilt or orientation of the plane in three-dimensional space.
How does the orientation of a plane change when you change the normal vector?
-When you change the normal vector, the plane twists and tilts along with it, maintaining a 90-degree angle with the normal vector.
What is the relationship between the normal vector and any vector lying in the plane?
-The normal vector is orthogonal to any vector lying in the plane, meaning their dot product is zero.
How do you find the vector from a fixed point on the plane to a generic point on the plane?
-You find the vector by subtracting the coordinates of the fixed point from the coordinates of the generic point, resulting in a vector that lies in the plane.
What is the equation of the plane in terms of the normal vector and a point on the plane?
-The equation of the plane is the dot product of the normal vector and the vector from the fixed point to any point on the plane, which equals zero.
What is the specific point and normal vector given in the example in the script?
-The specific point given is (1, 2, 3), and the normal vector given is (4, 5, 6).
How do you expand the dot product of the normal vector and the vector from the fixed point to a generic point?
-You expand it by multiplying the corresponding components of the two vectors and summing the results, as shown in the script: 4*(x-1) + 5*(y-2) + 6*(z-3).
What is the simplified component form of the equation of the plane given in the script?
-The simplified component form is 4x + 5y + 6z = 32, after moving all constants to the other side of the equation.
How does the script differentiate between the component form and the vector form of the equation of a plane?
-The script mentions that the equation derived is in component form, which involves coefficients and variables, in contrast to the vector form, which involves vectors and has not been taught yet.
What is the significance of the dot product being zero in the context of the plane's equation?
-The dot product being zero signifies that the normal vector is orthogonal to every vector in the plane, which is a fundamental property used to define the plane's equation.
Outlines
📚 Introduction to Plane Equations
The script introduces the concept of deriving equations for planes, building upon the previous work with line equations. It explains that, similar to lines, planes require two pieces of information: a point on the plane and a normal vector. The normal vector is perpendicular to the plane and dictates its orientation in three-dimensional space. The script uses a low-tech analogy with a paper plane and a pen to illustrate the concept of a normal vector.
📐 Understanding the Normal Vector and Plane Orientation
This paragraph delves deeper into the role of the normal vector in defining the orientation of a plane. It explains that the normal vector is orthogonal to any vector lying in the plane, using the dot product to demonstrate this orthogonality. The script describes the process of finding the vector from a fixed point on the plane to a generic point, and how the dot product of this vector with the normal vector must be zero, which is a key constraint in the equation of the plane.
🔍 Deriving the Equation of a Plane
The script outlines the steps to derive the equation of a plane using a specific point and a normal vector. It provides an example where a point on the plane is given as (1, 2, 3) and the normal vector is (4, 5, 6). The process involves calculating the vector from the fixed point to a generic point on the plane and then taking the dot product with the normal vector, setting it equal to zero. The script simplifies the resulting equation to its component form, demonstrating the mathematical process involved in finding the plane's equation.
Mindmap
Keywords
💡Equations for Planes
💡Point on the Plane
💡Normal Vector
💡Orthogonal
💡Dot Product
💡Vector
💡Component Form
💡Simplified Component Form
💡Three-Dimensional Space
💡Plane Orientation
💡Generic Point
Highlights
Introduction to extending the work on equations for lines to planes.
Requirement of two pieces of information for plane equations: a point on the plane and a normal vector.
Explanation of the normal vector as a vector that points directly away from the plane.
Illustration of the plane orientation using a pen as a normal vector.
Description of the orthogonal relationship between the normal vector and any vector lying in the plane.
Introduction of the generic point P on the plane and the vector from a fixed point to P.
The dot product constraint between the normal vector and the vector from P naught to P equals zero.
Demonstration of how to find the vector from a fixed point to a generic point on the plane.
Expansion of the dot product equation to form the plane's equation in component form.
Selection of a specific point P naught and a normal vector for the example.
Calculation of the vector components from P naught to P.
Derivation of the plane's equation using the dot product of the normal vector and the P naught to P vector.
Explanation of the component form of the plane's equation and its simplification.
Comparison between the component form and the vector form of the plane's equation.
Final equation of the plane with a point on the plane and the normal vector provided.
Emphasis on the importance of the normal vector in determining the plane's orientation in three dimensions.
Conclusion summarizing the method to write the equation of a plane given a point and a normal vector.
Transcripts
Browse More Related Video

Normal Vectors and Equations of Planes (Calculus 3)
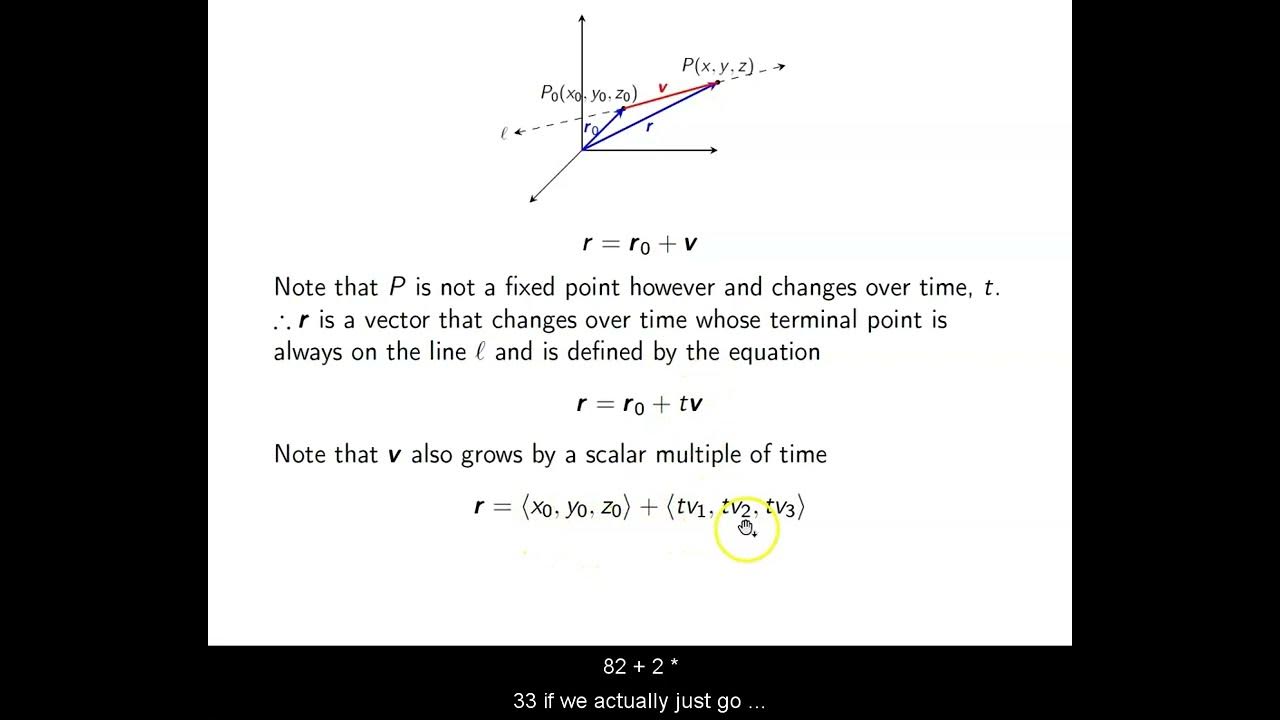
Ch. 9.6 Equations of Lines and Planes

Calculus 3: Equations of Lines and Planes (Video #5) | Math with Professor V

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V

How to find the component form of a vector

Tangent Planes (Calculus 3)
5.0 / 5 (0 votes)
Thanks for rating: