What is a tangent plane

Khan Academy
15 Jun 201603:20
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of tangent planes in the context of multivariable calculus, contrasting it with tangent lines in single-variable calculus. The narrator explains that while a tangent line touches a curve at a single point, a tangent plane barely kisses a 3D graph at a specified point. The script outlines the process of finding such a plane by selecting an input point on the graph and then determining a new linear function, L(x, y), whose graph corresponds to the tangent plane at that point. The upcoming videos promise to delve into the computation of tangent planes, emphasizing the geometric intuition and methodical approach similar to single-variable calculus.

Takeaways
  • 📚 The video series will focus on tangent planes of graphs in multivariable calculus, differentiating from other contexts like parametric surfaces.
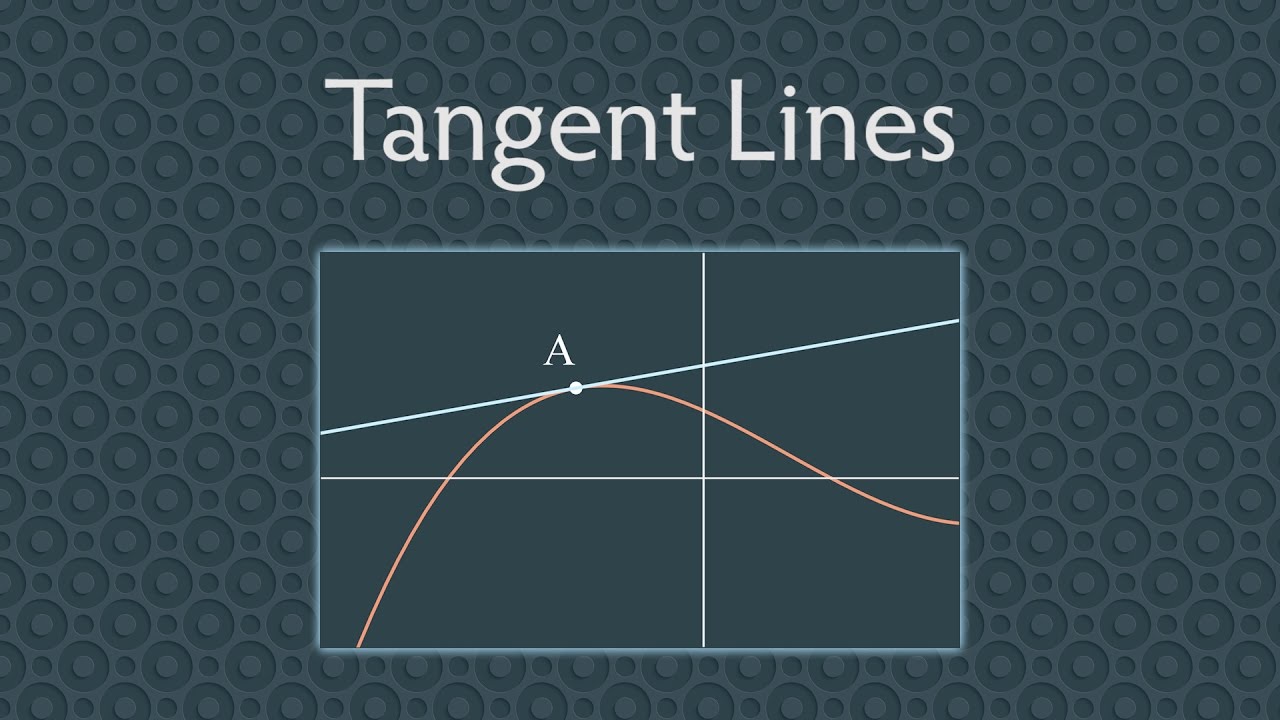
  • 📉 In single-variable calculus, finding the tangent line to a curve at a given point is a common problem, which helps in approximating the function around that point.
  • 📈 The concept of tangent planes in multivariable calculus is geometrically similar to finding tangent lines in single-variable calculus.
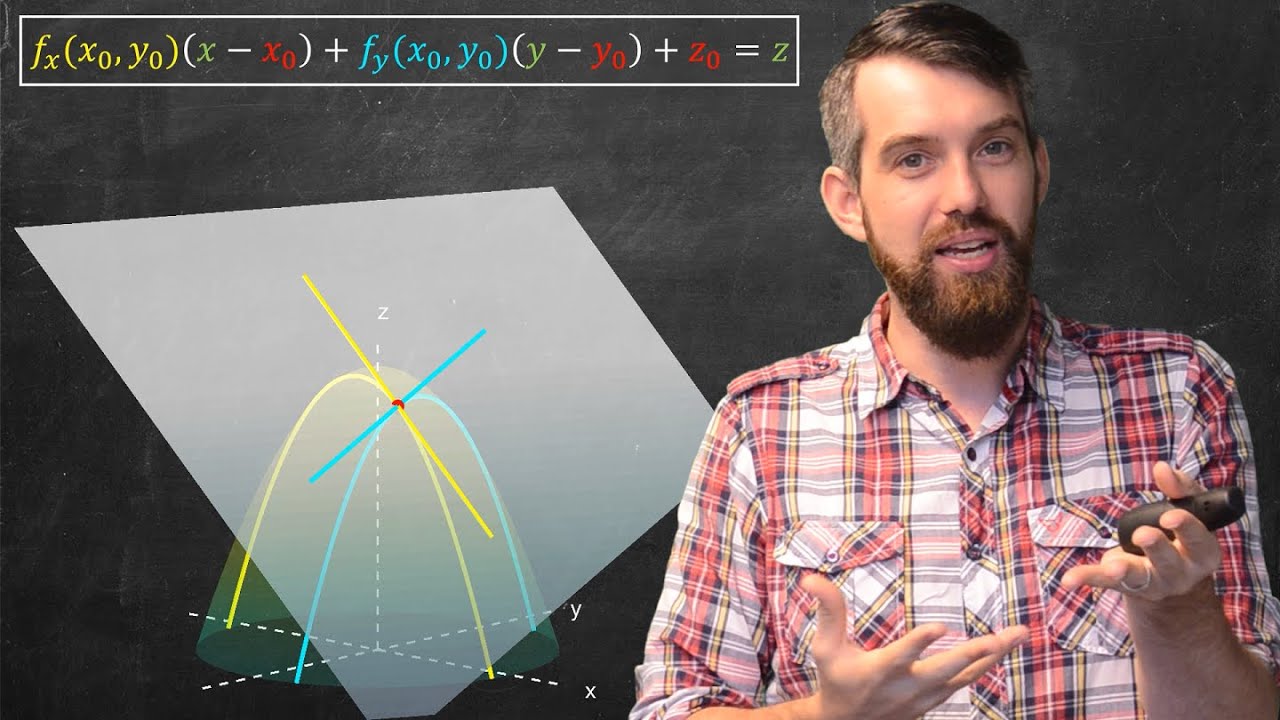
  • 🛤️ A tangent plane is a two-dimensional surface that barely touches the graph of a function at a specific point, unlike a one-dimensional tangent line.
  • 📍 The process of finding a tangent plane involves selecting an input point on the graph, which corresponds to a specific height or output of the function.
  • 🔍 The input point chosen for the tangent plane is represented by coordinates, such as \( x_0, y_0 \), in the multivariable context.
  • 🌐 The goal is to find a new function, denoted as \( L \), which represents the tangent plane at the chosen point.
  • 🔧 The function \( L \) will be dependent on the original function and the chosen input point, aiming to create a plane that is tangent to the graph at that point.
  • 🚀 The upcoming videos will explain the computation of the tangent plane, which might seem complex but is approached step by step, similar to single-variable problems.
  • 📚 The video aims to demystify the concept by breaking it down and comparing it to familiar single-variable calculus concepts.
  • 🔄 The process involves understanding the geometric intuition behind tangent planes and applying it to multivariable functions.
Q & A

  • What is the main topic of the video series?

    -The main topic of the video series is discussing tangent planes of graphs in the context of multivariable calculus.

  • Why are tangent planes different from tangent lines?

    -Tangent planes are different from tangent lines because they are two-dimensional surfaces that just barely touch the graph of a function, as opposed to one-dimensional lines in single-variable calculus.

  • What is the geometric intuition behind tangent planes in multivariable calculus similar to?

    -The geometric intuition behind tangent planes in multivariable calculus is similar to that of tangent lines in single-variable calculus, where both just barely touch the graph of a function at a specific point.

  • How does the concept of a tangent plane relate to approximating a function around a given point?

    -In single-variable calculus, the equation of a tangent line can be used to approximate the function around a given point. Similarly, in multivariable calculus, a tangent plane can be used for approximation purposes around a given point in a two-dimensional surface.

  • What is the first step in finding a tangent plane to a graph of a function?

    -The first step in finding a tangent plane to a graph of a function is to specify the input point where the tangent plane will touch the graph, similar to identifying the input value in single-variable calculus.

  • How does the input point in multivariable calculus differ from that in single-variable calculus?

    -In multivariable calculus, the input point is denoted by multiple variables, such as x0, y0, whereas in single-variable calculus, it is a single value, like x0.

  • What is the purpose of the new function L in the context of finding a tangent plane?

    -The purpose of the new function L is to represent the equation of the tangent plane, which will take in x and y as inputs and will have its graph as the tangent plane at the specified point.

  • What is the relationship between the function L and the original function of the graph?

    -The function L, which represents the tangent plane, is dependent on the original function of the graph and the input point where the tangent plane touches the graph.

  • Why might the process of finding a tangent plane seem intimidating at first?

    -Finding a tangent plane might seem intimidating because it involves controlling a three-dimensional plane, which is more complex than dealing with a one-dimensional line in single-variable calculus.

  • What approach does the video suggest for overcoming the intimidation of finding a tangent plane?

    -The video suggests taking the process one step at a time, drawing parallels to the single-variable case, and breaking down the problem into manageable parts.

Outlines
00:00
📚 Introduction to Tangent Planes of Graphs

This paragraph introduces the concept of tangent planes in the context of multivariable calculus, contrasting it with the more familiar notion of tangent lines in single-variable calculus. The speaker clarifies that the focus is on tangent planes to graphs, not other mathematical surfaces. The analogy is drawn between the tangent line's relationship to a curve in one dimension and the tangent plane's relationship to a graph in two dimensions. The paragraph sets the stage for a series of videos that will delve into how to find these tangent planes, starting with the selection of a specific input point and the geometric intuition behind the concept.

Mindmap
Keywords
💡Tangent Planes
A tangent plane is a geometric concept that represents a flat surface touching a three-dimensional graph at a single point without crossing it. In the context of the video, tangent planes are analogous to tangent lines in single-variable calculus but extend to multivariable functions where the graph is not a curve but a surface. The script discusses how to find the tangent plane to a graph of a function at a specific point, which is integral to understanding the local behavior of multivariable functions.
💡Multivariable Calculus
Multivariable calculus is a branch of mathematics that deals with functions of multiple variables, extending the concepts of single-variable calculus to more dimensions. The video script uses this term to distinguish the topic from single-variable calculus, emphasizing the study of functions with more than one input variable. The concept of tangent planes is a fundamental part of this field, as it helps in approximating the behavior of functions near a given point.
💡Graphs
In the script, graphs refer to the visual representation of functions, where one or more input variables are plotted against the output variable. The video focuses on the tangent planes of these graphs, which are surfaces that touch the graph at a specific point. The concept is used to explain how to find the tangent plane to a multivariable function's graph, which is a key part of understanding the local linear approximation of the function.
💡Tangent Line
A tangent line is a straight line that touches a curve at a single point without crossing it. The video script contrasts this with the tangent plane, indicating that while a tangent line is one-dimensional, a tangent plane is two-dimensional. The concept is fundamental in single-variable calculus and serves as a basis for understanding the more complex tangent planes in multivariable calculus.
💡Function Approximation
Function approximation is the process of finding a simpler function that closely resembles a more complex one, especially near a specific point. In the script, the tangent line provides an approximation in single-variable calculus, and by extension, the tangent plane serves a similar purpose in multivariable calculus. The video discusses how the tangent plane can be used to approximate the function around a given point, which is a practical application of the concept.
💡Input Point
An input point, often denoted as x₀ or (x₀, y₀) in the script, is a specific location in the domain of a function where the value of the function is of interest. The video script explains that to find a tangent plane, one must first specify the input point at which the tangent plane will touch the graph of the function. This point is crucial for determining the location and orientation of the tangent plane.
💡Parametric Surface
A parametric surface is a surface defined by a set of parametric equations, which are functions of one or more parameters. The script briefly mentions parametric surfaces to contrast them with the graphs of functions that are the main focus of the video. While tangent planes to parametric surfaces are a different context, the script clarifies that the discussion is specifically about tangent planes to graphs of functions.
💡Linear Function
A linear function is a function that represents a straight line or, in multiple dimensions, a flat surface. In the script, the term 'L' is used to denote a new function that is sought after, which is linear and whose graph is the tangent plane. The linear function is essential for finding the equation of the tangent plane at a given point on the graph of a multivariable function.
💡Three Dimensions
The term 'three dimensions' refers to the spatial context in which the video's mathematical concepts are visualized. The script explains that controlling a plane in three dimensions can be intimidating but is similar to the process in single-variable calculus. The three-dimensional space is where the graph of a multivariable function and its tangent plane are situated.
💡Geometric Intuition
Geometric intuition is the ability to understand and visualize geometric concepts and relationships. The script emphasizes that the geometric intuition used to understand tangent lines in single-variable calculus is almost identical when applied to tangent planes in multivariable calculus. This intuition is crucial for visualizing and comprehending the relationship between the graph of a function and its tangent plane.
💡Local Behavior
Local behavior refers to the properties or characteristics of a function near a specific point, as opposed to its global behavior across its entire domain. The video script discusses how the tangent plane provides insight into the local behavior of a multivariable function, indicating how the function behaves in the vicinity of the input point where the tangent plane touches the graph.
Highlights

Introduction to the concept of tangent planes of graphs in multivariable calculus.

Clarification that the focus is on graphs, not other contexts such as parametric surfaces.

Comparison of finding tangent lines in single variable calculus to tangent planes in multivariable calculus.

Explanation of the geometric intuition behind tangent planes being similar to tangent lines.

Description of a tangent plane as a two-dimensional surface that barely kisses the graph of a function.

Discussion on the ability to move the tangent plane around the graph of a function at different points.

The problem framing for finding a tangent plane involves specifying an input point.

Identification of the input point on the graph and its corresponding function output.

The goal of finding a new function, denoted as L, that represents the tangent plane.

The new function L is dependent on the original function and the chosen input point.

Introduction of the process to compute the tangent plane in upcoming videos.

Assurance that the computation of tangent planes, though seemingly complex, follows a step-by-step approach similar to single variable calculus.

Promise of a detailed explanation in the next videos on how to actually compute the tangent plane.

Highlighting the importance of understanding the geometric intuition behind tangent planes.

Emphasis on the practical applications of tangent planes, such as function approximation.

The significance of the tangent plane in approximating the function around a given point.

The anticipation of the next video where the computation process will be discussed in detail.

Transcripts

Browse More Related Video

How to find the TANGENT PLANE | Linear approximation of multi-variable functions

Computing a tangent plane

Controlling a plane in space

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V

The Tangent Line and the Derivative (Calculus)

Saddle points

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Tangent PlanesMultivariable CalculusFunction GraphsGeometric IntuitionCurve ApproximationLinear ApproximationSurface GeometryParametric SurfacesInput PointsEducational ContentMathematical Analysis