Chemical Kinetics practice problems - complete review
TLDRThis tutorial delves into chemical kinetics, explaining the concept as the study of reaction rates and factors influencing them, such as temperature and concentration. It covers the calculation of reaction rates, integrated rate laws for zero, first, and second-order reactions, and determining reaction orders from experimental data. The script also explores practical applications, including using half-life concepts to estimate the age of the Dead Sea Scrolls based on carbon-14 decay, a first-order process.
Takeaways
- 🔍 Chemical kinetics is the study of the rate at which chemical reactions occur, focusing on how fast or slow reactants convert into products.
- ⏱ The rate of a chemical reaction can be expressed in terms of the change in concentration of reactants or products over time, with units typically being molar per second.
- 📉 For a given reaction, the rate can be determined by the stoichiometric coefficients, where reactant rates may be negative and product rates positive, reflecting their consumption or formation, respectively.
- 🔑 Understanding the factors that affect reaction rates, such as temperature, concentration, pressure, and surface area, is crucial as they influence the frequency and energy of molecular collisions.
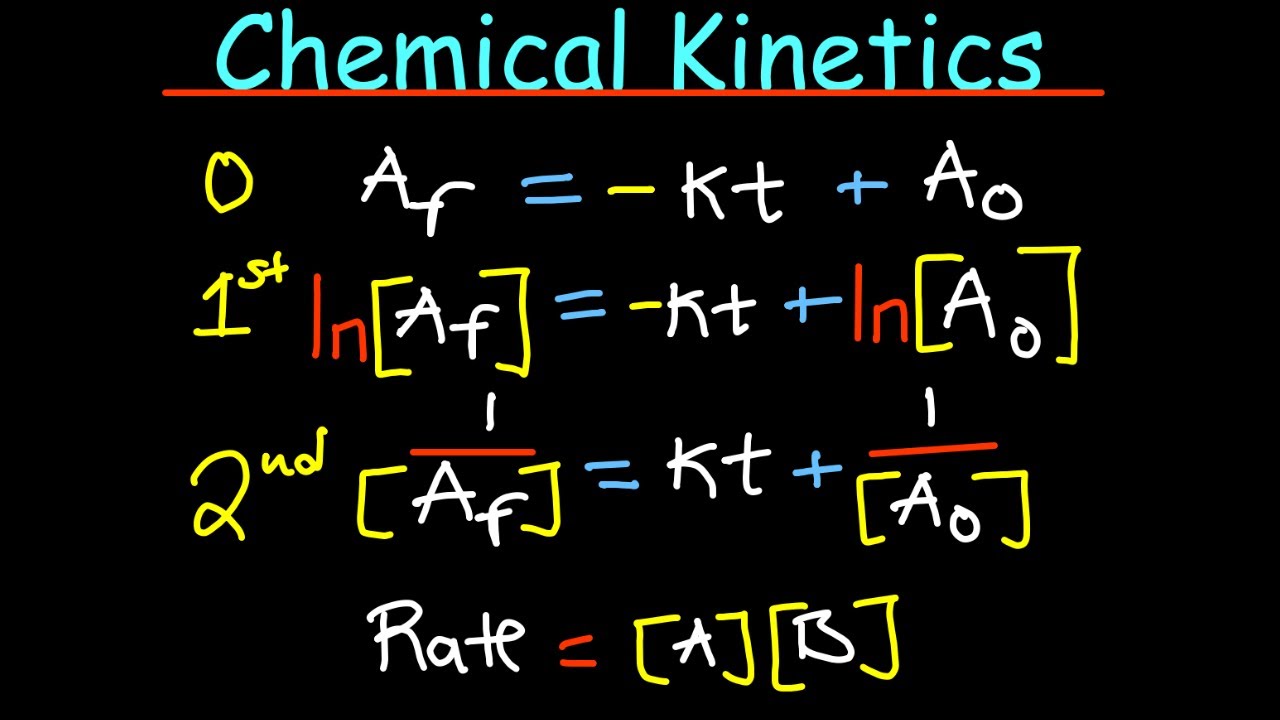
- 📚 Integrated rate laws are essential for determining the order of reactions and are applied to zero, first, and second-order reactions, each with its distinct graphical representation.
- 📈 Zero-order reactions graph as a straight line when concentration is plotted against time, indicating a constant rate regardless of concentration changes.
- 📊 First-order reactions are characterized by a graph of the natural log of concentration against time, showing a gradual decrease in reaction rate as reactants deplete.
- 📉 Second-order reactions have a graph where the reciprocal of concentration is plotted against time, typically showing a curve that ascends as the reaction progresses.
- 🧪 The tutorial provides step-by-step calculations for determining rate constants and half-lives from given data, exemplifying how to apply integrated rate laws to experimental results.
- ✂️ The Dead Sea Scrolls example illustrates the application of first-order decay kinetics to carbon-14 dating, emphasizing the relationship between decay rate constants and half-life to estimate the age of ancient artifacts.
Q & A
What is chemical kinetics and why is it important?
-Chemical kinetics is the study of the rate at which a chemical reaction proceeds. It is important because it helps us understand how fast or slow a reaction occurs, which is crucial in various fields such as chemistry, engineering, and environmental science.
How is the rate of a chemical reaction expressed in terms of reactants and products?
-The rate of a chemical reaction can be expressed in terms of the change in concentration of reactants or products over time. For reactants, it is typically a negative rate because their concentration decreases, while for products, it is positive as their concentration increases.
What are the units for the rate of a chemical reaction when dealing with concentration and time?
-The units for the rate of a chemical reaction are molar per second (M/s). This is because concentration is measured in moles (M) and time in seconds (s).
What is the collision theory, and how does it relate to the rate of a chemical reaction?
-The collision theory states that for a chemical reaction to occur, particles must collide with sufficient energy. The rate of a chemical reaction is influenced by factors that affect the frequency and energy of these collisions, such as temperature, concentration, and pressure.
How does an increase in temperature affect the rate of a chemical reaction according to the kinetic theory?
-An increase in temperature leads to an increase in the kinetic energy of the particles, causing them to move faster and collide more frequently. This results in a higher rate of chemical reactions.
What is the relationship between the concentration of reactants and the rate of a chemical reaction?
-An increase in the concentration of reactants generally leads to an increase in the rate of a chemical reaction because there is a higher probability of particle collisions, thus more opportunities for the reaction to occur.
How does pressure affect the rate of a reaction involving gaseous reactants or products?
-An increase in pressure leads to a decrease in volume if the temperature is constant (according to the ideal gas law). In a smaller volume, gas particles are closer together, resulting in more frequent collisions and thus an increased rate of reaction.
What is the significance of surface area in the rate of a chemical reaction involving solid particles?
-An increase in the surface area of solid particles increases the rate of a chemical reaction because there are more sites available for collisions to occur, leading to a higher frequency of successful reactions.
What are integrated rate laws, and how are they used to determine the order of a reaction?
-Integrated rate laws are mathematical equations that relate the concentration of reactants or products to time for different orders of reactions (zero, first, and second order). They are used to plot graphs of concentration versus time, from which the order of a reaction can be determined by the gradient and shape of the graph.
How can you calculate the half-life of a first-order reaction?
-The half-life (t1/2) of a first-order reaction can be calculated using the formula t1/2 = ln(2) / k, where k is the rate constant of the reaction. This formula is derived from the integrated rate law for first-order reactions.
What is the significance of the order of a reaction in determining the rate constant and the reaction mechanism?
-The order of a reaction indicates how the rate depends on the concentrations of the reactants. It helps in determining the rate constant (k) and understanding the reaction mechanism by showing the relationship between the reactant concentrations and the rate at which the reaction proceeds.
How can you determine the instantaneous rate of a chemical reaction at a specific time?
-The instantaneous rate at a specific time can be determined by finding the slope of the tangent to the concentration-time graph at that time point. The steeper the tangent, the higher the instantaneous rate of the reaction.
What is the concept of specific activity in the context of carbon-14 dating?
-Specific activity refers to the activity of a radioactive isotope per unit mass, such as the number of decays per second per gram. In the context of carbon-14 dating, it is used to measure the remaining activity of carbon-14 in a sample, which helps determine its age.
How can you calculate the approximate age of a sample using carbon-14 dating?
-The approximate age of a sample can be calculated using the first-order decay equation for carbon-14. By measuring the specific activity of carbon-14 in the sample and comparing it to the initial activity, you can determine the number of half-lives that have passed, which gives you the age of the sample.
Outlines
🔍 Introduction to Chemical Kinetics
This paragraph introduces the concept of chemical kinetics, which is the study of the rate at which chemical reactions occur. It explains that chemical kinetics involves understanding how fast or slow a reaction progresses. The paragraph outlines the basic principles, such as the rate of reaction being expressed in terms of the change in concentration of reactants or products over time, and the importance of stoichiometric coefficients in these expressions. It also touches on the units used to measure reaction rates, which are typically moles per second (M/s).
🔧 Factors Affecting Reaction Rates
This section delves into the factors that influence the rate of chemical reactions. It discusses the collision theory, which posits that for a reaction to occur, particles must collide with sufficient energy. The paragraph explores how factors such as temperature, concentration, pressure, and surface area can affect the frequency and energy of these collisions, thereby influencing the reaction rate. It also introduces the concept of reaction orders and integrated rates, which are essential for understanding and predicting the behavior of chemical reactions.
📚 Understanding Reaction Rates and Kinetics
The paragraph focuses on defining reaction rates and distinguishing between different types of rates, including instantaneous rate, initial rate, and average rate. It provides a detailed explanation of how to calculate these rates and the significance of each in the context of a chemical reaction. Additionally, it discusses the concept of half-life and how it relates to first-order reactions, providing a formula for calculating the half-life and emphasizing the importance of understanding the units for rate constants in kinetic studies.
🧪 Calculation of Rate Constants and Half-Life
This section presents a problem-solving approach to calculate the rate constant and half-life for a first-order reaction. It uses a given scenario where a reaction is 8.5% complete after 480 seconds to demonstrate the calculation process. The paragraph walks through the steps of using the integrated rate law for first-order reactions to find the rate constant and then uses this constant to determine the half-life of the reaction.
📉 Determining Reaction Orders from Data
The paragraph discusses how to determine the order of a reaction with respect to each reactant and the overall reaction order using experimental data. It explains the process of comparing different trials with varying concentrations of reactants and how the rate of the reaction changes accordingly. The method involves creating and solving equations based on the rate law to find the orders (m and n) for each reactant involved in the reaction.
📝 Rate Law and Reaction Orders in Practice
This section provides a practical example of how to apply the concepts of rate laws and reaction orders to experimental data. It demonstrates the process of finding the rate constant for a reaction involving hemoglobin and carbon monoxide, using a table of initial rates from various experiments. The paragraph shows how to calculate the orders of the reaction with respect to each reactant and then use these values to derive the overall rate law and rate constant.
📈 Plotting Concentration-Time Graphs
The paragraph describes the process of plotting concentration-time graphs for chemical reactions, using the decomposition of hydrogen iodide as an example. It provides guidance on selecting appropriate scales for the graph and how to plot the data points. The paragraph also explains how to calculate the average rate of reaction between two time points from the graph and how to determine the instantaneous rate at a specific time by drawing a tangent to the curve.
🕰️ Calculating Instantaneous Rates
This section explains how to calculate the instantaneous rate of a reaction at a given time by using the concept of a tangent to the concentration-time graph. It illustrates the method of finding two points on the tangent line and then calculating the gradient of the line to determine the instantaneous rate at a specific time point, such as 200 seconds into the reaction.
📚 First-Order Decay and Radiocarbon Dating
The final paragraph discusses the application of first-order decay in radiocarbon dating, specifically using the example of the Dead Sea Scrolls. It explains how the specific gravity of Carbon-14 in the sample is compared to that in living material to determine the age of the artifact. The paragraph outlines the steps to calculate the decay constant (k) from the half-life of Carbon-14 and then use this constant to find the approximate age of the sample.
🔚 Conclusion and Preview of Future Content
The concluding paragraph summarizes the key points covered in the tutorial, emphasizing the importance of understanding rate laws, integrated rate equations, and half-life formulas. It also provides a preview of upcoming content, which will focus on activation energy and the Arrhenius equation, indicating a continuation of the exploration of chemical kinetics in more depth.
Mindmap
Keywords
💡Chemical Kinetics
💡Reaction Rate
💡Stoichiometric Coefficients
💡Collision Theory
💡Integrated Rate Laws
💡Half-Life
💡Concentration
💡Temperature
💡Pressure
💡Surface Area
💡Activation Energy
Highlights
Chemical kinetics is the study of the rate at which chemical reactions progress.
The rate of a chemical reaction can be expressed in terms of reactants or products' concentration changes over time.
Understanding stoichiometric coefficients is key to calculating reaction rates correctly.
The rate of reaction is always positive as it indicates the increase or decrease in concentration over time.
Factors such as temperature, concentration, pressure, and surface area can affect the rate of a chemical reaction.
Collision theory explains that chemical reactions occur when particles collide with sufficient energy.
Integrated rate laws are used to determine the order of reactions and calculate rate constants.
Zero-order reactions have a linear relationship between time and concentration on a graph.
First-order reactions are characterized by a graph of time against the natural log of concentration.
Second-order reactions show a reciprocal relationship between concentration and time on a graph.
The instantaneous rate is the reaction rate at any given point in time during the reaction.
The initial rate is the reaction rate at the very start of the reaction.
The average rate is calculated over a specific time period during the reaction.
A first-order reaction's rate constant can be determined using the natural log of the concentration ratio over time.
The half-life of a reaction can be calculated using the natural log of 2 divided by the rate constant for first-order reactions.
The overall order of a reaction is the sum of the individual orders of the reactants involved.
The rate law can be determined by analyzing the effect of changing reactant concentrations on the reaction rate.
The Dead Sea Scrolls' age can be approximated using the first-order decay of carbon-14 and its specific gravity.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: